Review-Estimation

• Parameter : we wish to estimate the parameter $\theta$ from the observation(s) $x$. Theses can be vectors
  $\theta=[\theta_1, \theta_2, \cdots, \theta_p]^T$ and
  $x=[x[0], x[1],\cdots,x[N-1]]^T$ or scalars.
• Parmetrized PDF : the unknown parameter $\theta$ is to be estimated. $\theta$ parametrizes the probability density function of the received data $p(x;\theta)$.
• Estimator : Rule or Function that assigns a value $\hat \theta$ to $\theta$ for each realization of $x$.
• Estimate : Value of $\theta$ obtained for a given realization of $x$. $\hat \theta$ will be used for the estimate, while $\theta$ will represent the true value of the unknown paramete.
• Mean and Variance of the estimator : $E(\hat \theta)$ and $var(\hat \theta) = E\left[(\hat \theta - E(\hat \theta))^2 \right]$.
  Expectations are taken over $x$ (meaning $\hat \theta$ is random, not $\theta$.)

Unbiased Estimators

• An estimator $\hat \theta$ is called unbiased, if $E(\hat \theta) = \theta$ for all possible $\theta$.
  $\hat \theta = g(x) \rightarrow E(\hat \theta) = \int g(x)p(x;\theta)dx = \theta$
• If $E(\hat \theta) \neq \theta$, the bias is $b(\theta) = E(\hat \theta) - \theta$
  (Expectation is taken with respect to $x$ or $p(x;\theta)$)

Revisit example of the DC level in noise, two candidate estimators
$\hat A=\frac{1}{N}\displaystyle \sum_{n=0}^{N-1}x[n]$ (Sample mean) and $\widecheck{A} = x[0]$ (First sample value)
are unbiased since $E(\hat A) = E(\widecheck A) = A$

• $E(\hat \theta) = \theta$ may hold for some values of $\theta$ for biased estimators, i.e., modified sample mean estimator
  $\widecheck{A} = \frac{1}{2N}\sum_{n=0}^{N-1} x[n] \rightarrow E(\widecheck{A}) = \frac{1}{2}A \left\{ \begin{array}{ll} = A & \text{if } A = 0 \\ \neq A & \text{if } A \neq 0 \end{array} \right. \rightarrow \;biased$

  An Unbiased estimator is not necessarily a good estimator;
  But a biased estimator is a poor estimator.

Mean-Squared Error(MSE) Criterion

$mse(\hat \theta) = E\left[(\hat \theta-\theta)^2\right]\\ =E\left\{\left[(\hat \theta -E(\hat \theta)) + (E(\hat \theta) - \theta)\right]^2\right\}\\ =var(\hat \theta) + [E(\hat \theta) - \theta]^2\\[0.2cm] =var(\hat \theta) + b^2(\theta)$

• $\hat \sigma^2=\frac{1}{N}\displaystyle\sum_{n=0}^{N-1}(x[n]-\bar x)^2,\;\bar x:sample \; mean$

• $E[x[n]] = \mu,\;Var[x[n]] = \sigma^2=E[x^2[n]]-E^2[x[n]],\;E[x^2[n]]=\textcolor{red}{\sigma^2+\mu^2 \cdots(*)}$

• $Var(\bar x) = \frac{\sigma^2}{N} = E[\bar x^2]-\mu^2 \rightarrow E[\bar x^2] = \textcolor{red}{\frac{\sigma^2}{N}+\mu^2\cdots(**)}$

• $E[\hat \sigma ^2] \\= \frac{1}{N}E\left[ \displaystyle \sum_{n=0}^{N-1}(x^2[n]) -2\bar x\displaystyle\sum_{n=0}^{N-1}x[n]+N\bar x^2\right]\\ =\frac{1}{N}E\left[ \displaystyle \sum_{n=0}^{N-1}x^2[n]-\textcolor{blue}{N\bar x^2}\right]\\ =\frac{1}{N}(\displaystyle\sum_{n=0}^{N-1}(E[x^2[n]]) - NE[\bar x^2])\\[0.5cm] =\frac{1}{N}\left(\displaystyle\sum_{n=0}^{N-1}(E[x^2[n]]\textcolor{red}{\cdots(*)}\right) - N\left(E[\bar x^2]\textcolor{red}{\cdots(**)}\right)\\ =\frac{1}{N}\left(N\times(\sigma^2 +\mu^2) - N(\frac{\sigma^2}{N} + \mu^2)\right)\\ =\frac{1}{N}(N\sigma^2 - \sigma^2)\\[0.3cm] =\frac{N-1}{N}\sigma^2 \textcolor{red}{\cdots "biased\; estimator"}$

• Note that, in many cases, minimum MSE criterion leads to unrealizable estimator, which cannot be written solely as a function of the data, i.e.,
  $\widecheck A = a\dfrac{1}{N}\displaystyle\sum_{n=0}^{N-1}x[n]$, where $a$ is chosen to minimize MSE
  Then, $E(\widecheck A) = aA,\; var(\widecheck A) = \dfrac{a^2\sigma^2}{N} \rightarrow mse(\widecheck A) = \dfrac{a^2\sigma^2}{N}+(a-1)^2A^2$

  $\dfrac{dmse(\widecheck A)}{da} = \dfrac{2a\sigma^2}{N}+2(a-1)A^2 =0\\[0.3cm] \rightarrow a_{opt} = \dfrac{A^2}{A^2 +\dfrac{\sigma^2}{N}}$

  Unrealizable, a function of unknown A

Unbiased Estimator...?

$\hat {\sigma^2}' = \dfrac{1}{N-1}\displaystyle\sum_{n=0}^{N-1}(x[n]-\bar x)^2 \rightarrow unbiased \;for\;sample \;variance$

Minimum Variance Unbiased Estimation(MVUE)

• Any criterion that depends on the bias is likely to be unrealizable
  $\rightarrow$ Practically minimum MSE estimator needs to be abandoned

Minimum variance unbiased(MVU) estimator

• Alternatively, contrain the bias to be zero
• Find the estimator which minimizes the variance (minimizing the MSE as well for unbiased case)
  $mse(\hat \theta) = var(\hat \theta) + b^2(\theta),\;E[b^2(\theta)] =0\\ \rightarrow var(\hat \theta)$

  Minimum variance unbiased(MVU) Estimator

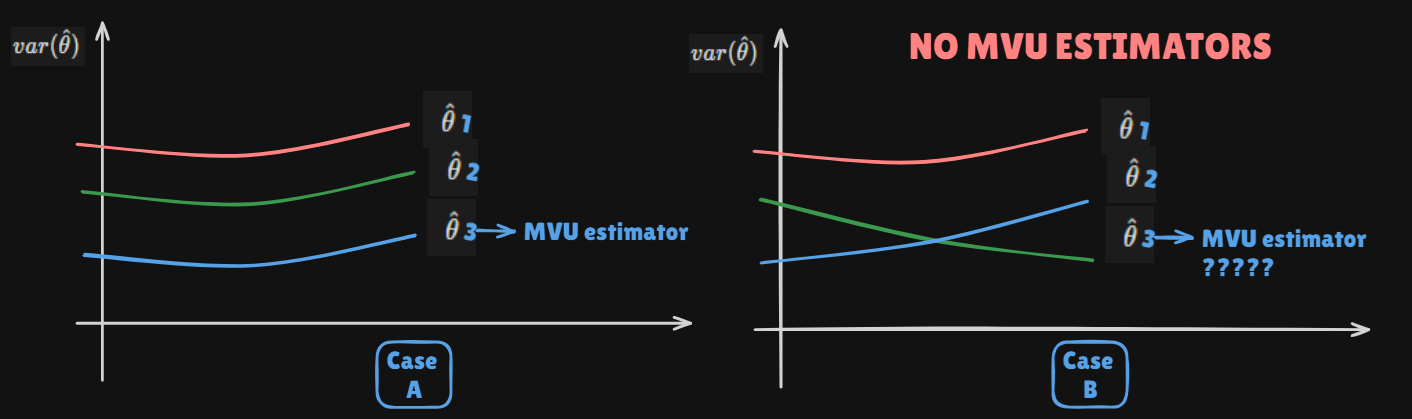
Existence of the MVU Estimator

• An unbiased estimator with minimum variance for all $\theta$
• Examples
  $\hat \theta$
  
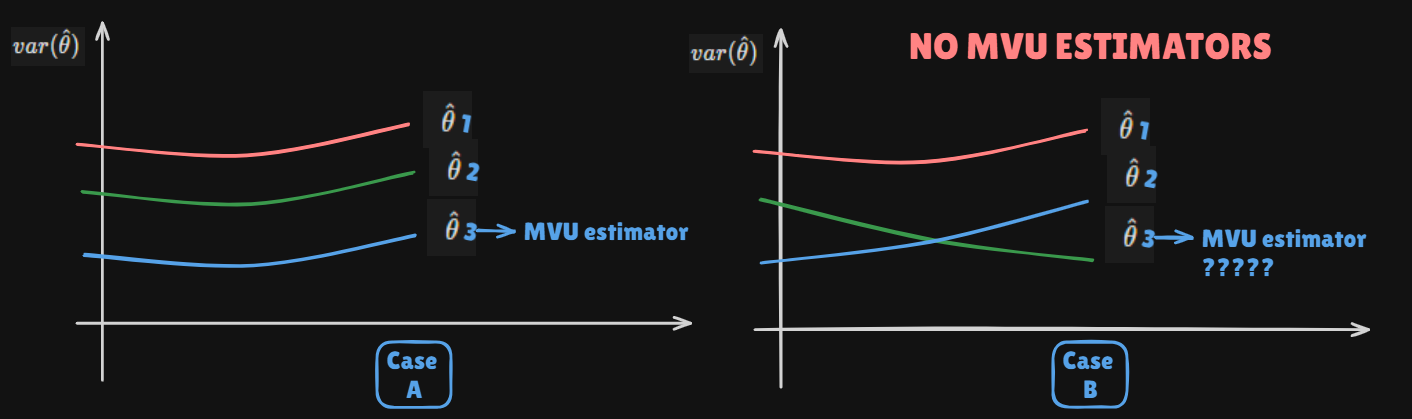
• There might be some problems

  • Problem 1 : We can not try All functions to find MVUE
  • Problem 2 : We can not try All theta intervals to confirm whether it minimizes variance or not

Fining the MVU Estimator

• There is no general framework to find MVU estimator even if it exists.

  Possible approaches:

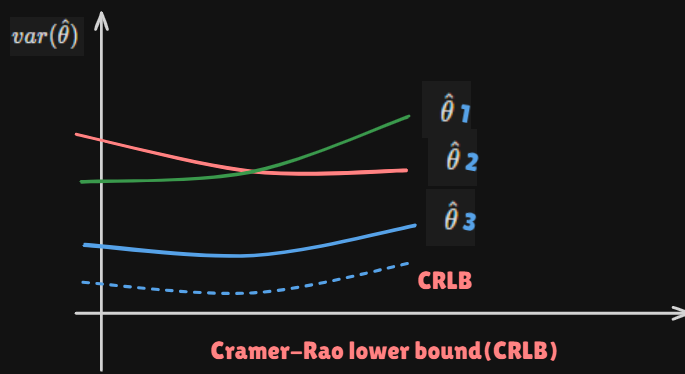
  • Determine the Cramer-Rao lower bound(CRLB) and check if some estimator satisfies it
  • Apply the Rao-Blackwell-Lehmann-Scheffe(RBLS) theorem
  • Find unbiased linear estimator with minimum variance(best linear unbiased estimator, BLUE)
    

All Content has been written based on lecture of Prof. eui-seok.Hwang in GIST(Detection and Estimation)