Detection and Estimation
1.[DetnEst] 1. Introduction to Statiscal Signal Processing
: Discrete set of hypotheses(right or wrong, Classification etc.): Continuous set of hypotheses(almost always wrong - minimize error instead)Bayesian
2.[DetnEst] 2. Minimum variance unbiased(MVU) estimator
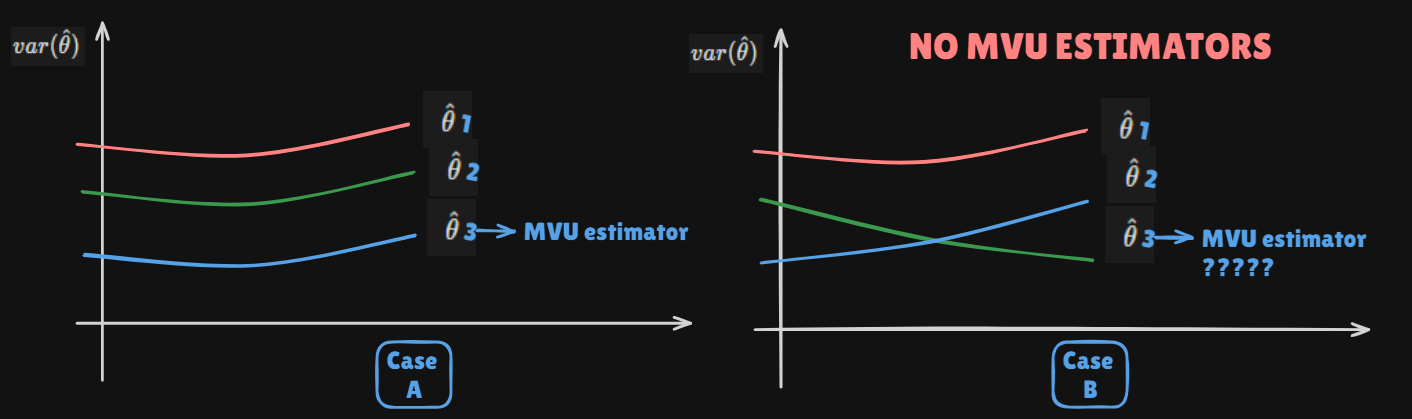
Parameter : we wish to estimate the parameter $\\theta$ from the observation(s) $x$. Theses can be vectors $\\theta=\\theta_1, \\theta_2, \\cdots, \\t
3.[DetnEst] Assignment 1

Let $X0, X_1, X_2, \\dots, X{N-1}$ be a random sample of $X$ having unknown mean $\\mu$ and variance $\\sigma^2$.Show that the estimator of variance d
4.[DetnEst] 3. Cramer-Rao Lower Bound(CRLB)
Mean Squared Error(MSE) criterion$$mse(\\hat \\theta) = E(\\hat \\theta -\\theta)^2 =var(\\hat \\theta) + b^2(\\theta)$$Note that, in many cases, mini
5.[DetnEst] Assignment 2

Suppose that $X0, X_1, X_2,\\dots,X{N-1}$ be a random sample of an exponential random variable $X$ with an unknown parameter $\\alpha$, corresponding
6.[DetnEst] 4. Linear Models and Extension
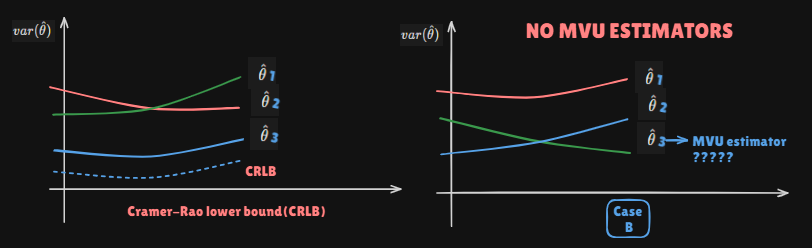
The CRLB give a lower bound on the variance of any unbiased estimatorDoes not guarantee bound can be obtainedIf find an unbiased estimator whose varia
7.[DetnEst] Assignment 3

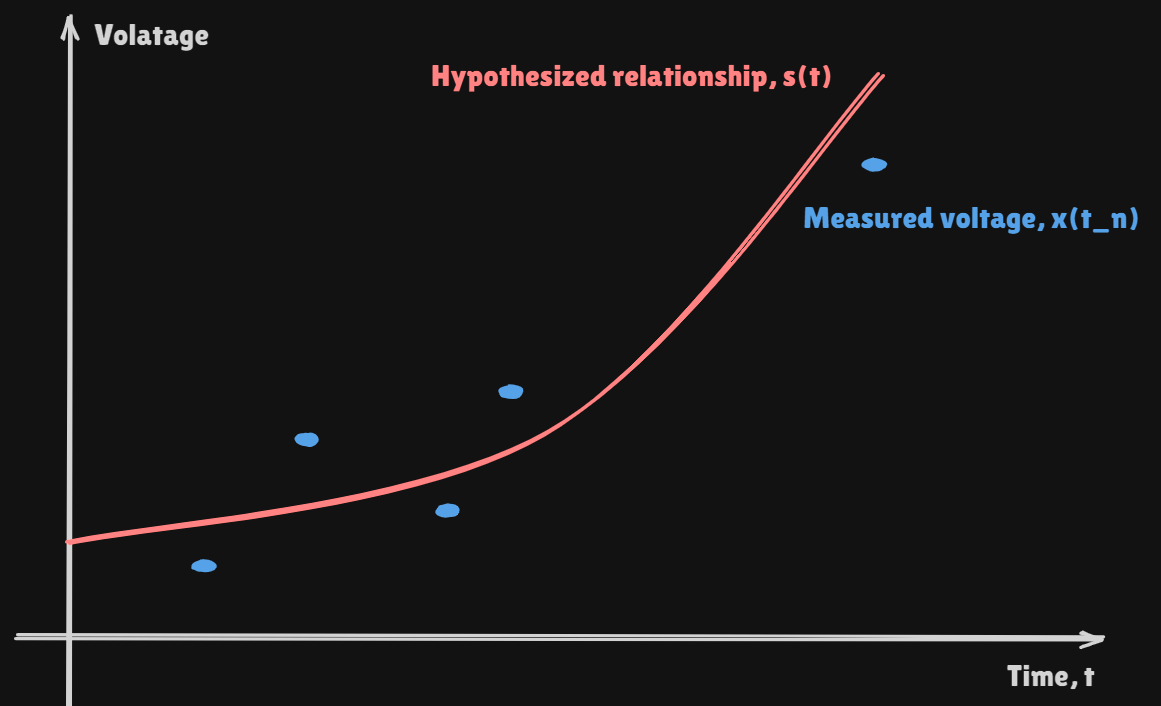
Given 3 data points $(t_0,x_0),\\;(t_1,x_1)$ and $(t_2,x_2)$We can have a second order polynomial, where 3 coefficients are unknownWhat is the best es
8.[DetnEst] 5. General MVUE
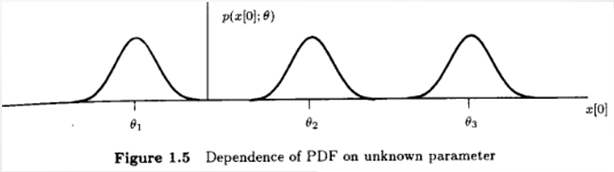
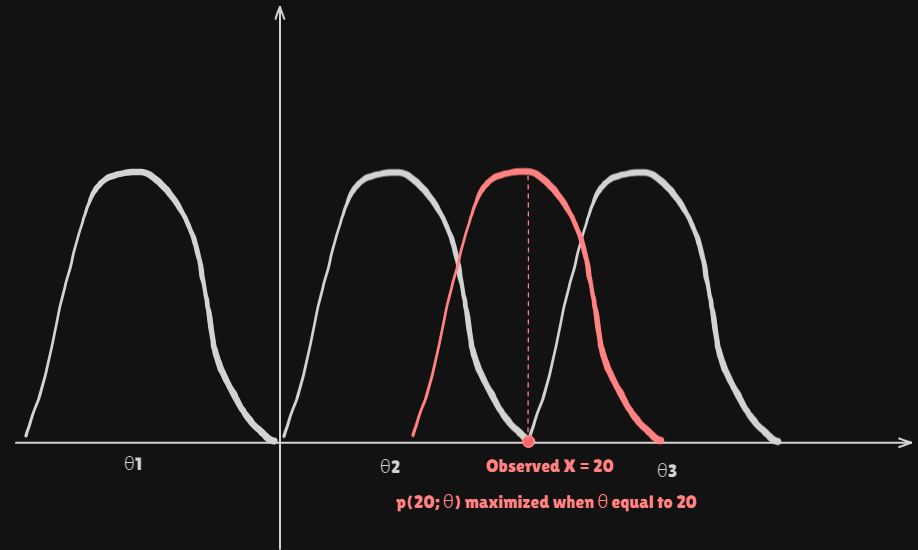
The Likelihood Function $p(x;\\theta)$ (same description of PDF)But as a function of parameter $\\theta$ w/ the data vector $x$ fixedIntuitively : sha
9.[DetnEst] Assignment 4

Suppose that $X_1$ and $X_2$ are independent Poisson random variables each with parameter $\\lambda$Let the parameter $\\theta$ by$$\\theta=e^{-\\lamb
10.[DetnEst] 6. Maximum Likelihood Estimation
When the observation and the data are related in a linear way $\\text{x}=\\text{H}\\theta+\\text{w}$And the noise was Gaussian, then the MVUE was easy
11.[DetnEst] Assignment 5

Let $(X0,X_1,\\dots,X{N-1})$ be a random sample of a Bernoulli random variable $X$ with a probability mass function$$f(x;p)=p^x(1-p)^{1-x}$$where $x\\
12.[DetnEst] 7. The Bayesian Philosophy

Up to now - Classical Approach : the parameter is a deterministic but unknown constantAssumes $\\theta$ is deterministicVariance of the estimate could
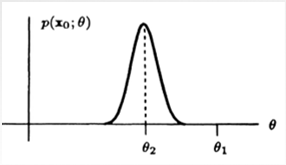
13.[DetnEst] 8. General Bayesian Estimators
PreviouslyIntroduced the idea of a a priori information on $\\theta\\rightarrow$ use prior pdf: $p(\\theta)$Defined a new optimality criterion $\\righ
14.[DetnEst] 9. Linear Bayesian Estimation
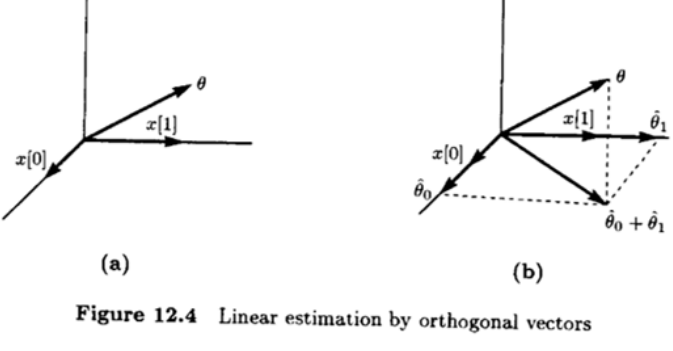
Overview In Chapter 11, General Bayesian estimators MMSE takes a simple form when $\text{x}$ and $\theta$ are jointly Gaussian $\rightarrow$ it is
15.[DetnEst] Assignment 6

Let $(X0,X_1,\\dots,X{N-1})$ be a normal random variable $X$ with maen $\\mu$ and variance $\\sigma^2$, where $\\mu$ is unknown. Assume that $\\mu$ is
16.[DetnEst] 10. Kalman Filters
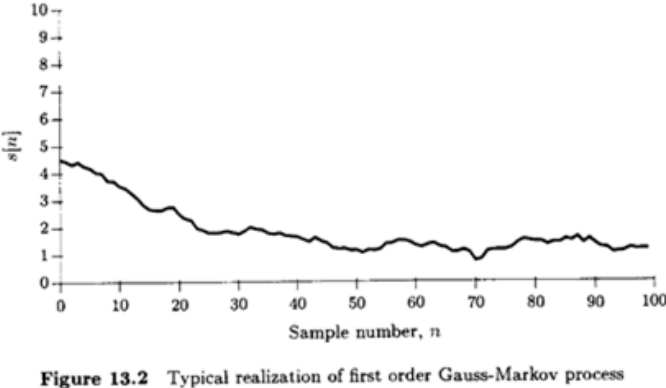
In 1960, Rudolf Kalman developed a way to solve some of the practical difficulties that arise when trying to apply Weiner filtersThe three keys to lea
17.[DetnEst] Assignment 7

Let $Y=X^2$, and let $X$ be a uniform random variable over $(-1, 1)$Find the linear minimum mean squared estimator of $Y$ in terms of $X$Find its mean
18.[DetnEst] 11. Statistical Decision Theory
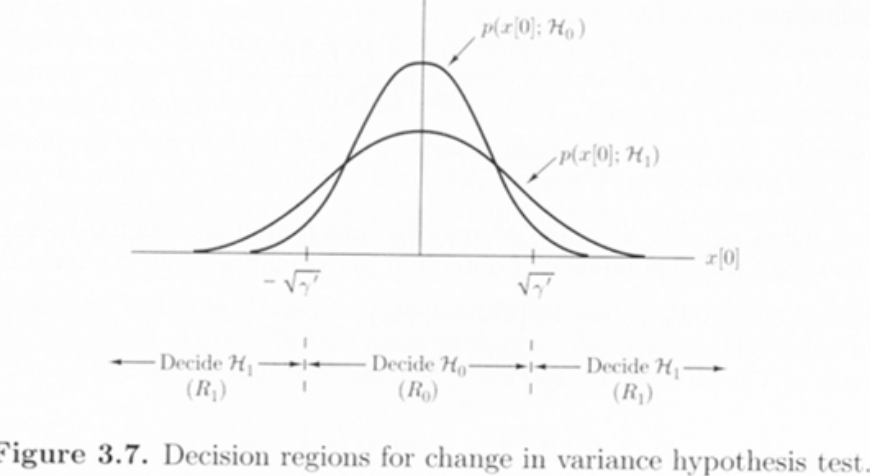
Estimation : Continuous set of hypotheses(almost always wrong - minimize error instead)Detection : Discrete set of hypotheses(right or wrong)Classical
19.[DetnEst] 12. Deterministic Signal Detection
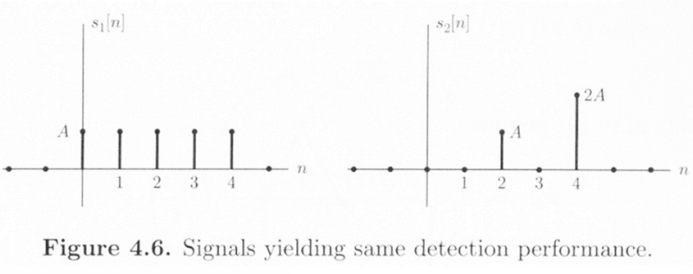
Detection of a known signal in Gaussian noiseNP criterion or Bayes risk criterionThe test statistic is a linear function of the data due to the Gaussi
20.[DetnEst] 13. Random Signal Detection
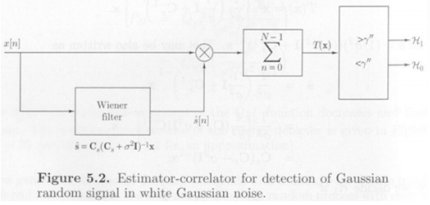
Neyman-Pearson criteria (max $PD$ s.t. $P{FA} =$ constant) : likelihood ratio test, threshold set by $P\_{FA}$Minimize Bayesian risk (assign costs to
21.[DetnEst] 14. Statistical Decision Theory : Final
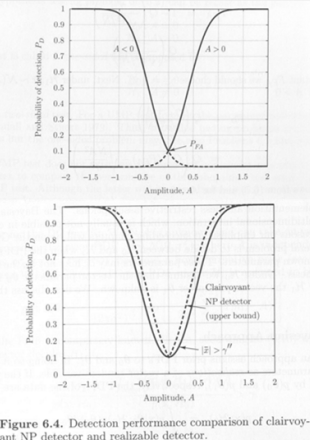
So far, detection underNeyman-Pearson criteria ( max $PD$ s.t. $P{FA}=$ constant $)$ : likelihood ratio test, threshold set by $P\_{FA}$Minimize Bayes
22.[DetnEst] Assignment 8

For the DC Level in WGN detection problem assume that we wish to have $P{FA}=10^{-4}$ and $P_D=0.99$If the SNR is $10\\log{10}A^2/\\sigma^2=-30\\text{
23.[DetnEst] Assignment 9

Show the NP detector for a Gaussian rank one signal as a Gaussian random process whose covariance matrix is $Cs=\\sigma^2_Ahh^T$ embedded in WGN with