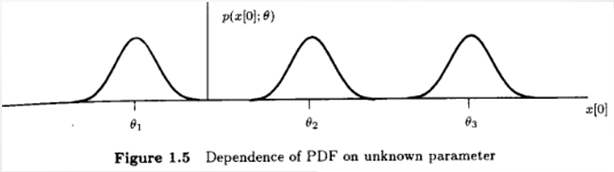
Recap

Revisit : Likelihood Function

• The Likelihood Function $p(x;\theta)$ (same description of PDF)
• But as a function of parameter $\theta$ w/ the data vector $x$ fixed

Likelihood Function Characteristics

• Intuitively : sharpness of the Likelihood Function sets accuracy
• Sharpness is measured using curvature :
  $-\left.\frac{\partial^2 \ln p(\mathbf{x}; \theta)}{\partial \theta^2}\right|_{\mathbf{x}=\mathbf{x}_0, \theta}$
• Curvature ↑ ⇒ PDF concentration ↑ ⇒ Accuracy ↑
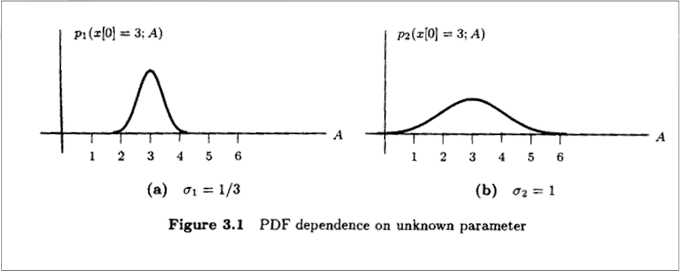
• Expected sharpness of likelihood function
  $-E\left[\left.\frac{\partial^2 \ln p(\mathbf{x}; \theta)}{\partial \theta^2}\right]\right|_\theta$

Vector Form of the CRLB

• Assuming $p(x;\theta)$ satisfies the regularity condition
  $E\left[\frac{\partial\ln p(x;\theta)}{\partial\theta}\right]=0,\quad\text{for all }\theta$
• The covariance matrix of any unbiased estimator $\hat\theta$ satisfies
  $C_{\hat\theta}-I^{-1}(\theta)\geq0\quad[I(\theta)]_{ij}=-E\left[\frac{\partial^2\ln p(x;\theta)}{\partial\theta_i\partial\theta_j}\right]$
  where $\geq 0$ means the matrix is positive semidefinite
• Furthermore, an unbiased estimator may be found that attains the bound
  $C_{\hat\theta}=I^{-1}(\theta)$ if and only if
  $\frac{\partial \ln p(x;\theta)}{\partial\theta}=I(\theta)(g(x)-\theta)$
• In that case, $\hat\theta=g(x)$ is the MVUE with variance $I^{-1}(\theta)$

MVUE for the Linear Model - Theorem

• If the observed data can be modeled as $\text{x}=H\theta+\text{w}$,
  $\frac{\partial\ln p(x;\theta)}{\partial\theta}=\frac{\text{H}^T\text{H}}{\sigma^2}[(\text{H}^T\text{H})^{-1}\text{H}^T\text{x}-\theta]$
• The MVUE is
  $\hat \theta=(\text{H}^T\text{H})^{-1}\text{H}^T\text{x}$
• And the covariance matrix of $\hat\theta$ is
  $C_{\hat\theta}=I^{-1}(\theta)=\sigma^2(\text{H}^T\text{H})^{-1}$
• For the linear model, the MVUE is efficient in that attains the CRLB
• Also, the statiscal performance of $\hat\theta$ is completely specified, because $\hat\theta$ is a linear transformation of a Gaussian vector $\text{x}$ and hence

  $\hat\theta\sim N(\theta, \sigma^2(\text{H}^T\text{H})^{-1})$

Finding the MVUE so far

• When the observations and the data are related in a linear way $\text{x}=\text{H}\theta+\text{w}$,
• and the noise was Gaussian, then the MVUE was easy to find:
  $\hat \theta=(\text{H}^T\text{H})^{-1}\text{H}^T\text{x}$
  with covariance matrix, $C_{\hat\theta}=I^{-1}(\theta)=\sigma^2(\text{H}^T\text{H})^{-1}$
• Using the CRLB, if you got lucky, then you could write
  $\frac{\partial \ln p(x;\theta)}{\partial\theta}=I(\theta)(g(x)-\theta)$
  where $\hat\theta=g(x)$ would be your MVUE, an efficient estimator(meet the CRLB)
• Even if no efficient estimator exists, an MVUE may exist
• In this section, we try to find a systematic way of determining the MVUE if it exists

Finding the MVUE

• We wish to estimate the parameter(s) $\theta$ from the observations $\text{x}$
  • Step 1
    • Determine (if possible) a sufficient statistic $T(x)$ for the parameter to be estimated $\theta$
    • This may be done using the Neyman-Fisher factorization theorem
  • Step 2
    • Determine whether the sufficient statistic is also complete

      This is generally hard to do

    • If it is not complete, we can say nothing more about the MVUE
    • If it is, continue to Step 3
  • Step 3
    • Find the MVUE $\hat\theta$ from $T(x)$ is one of two ways using the
      Rao-Blackwell-Lehmann-Scheffe(RBLS) theorem

      Rao-Blackwell-Lehmann_Scheffe(RBLS) theorem

      • Find a function $g(\cdot)$ of the sufficient statistic that yields an unbiased estimator $\hat\theta = g(T(x))$, the MVUE
      • By definition of completeness of the statistic, this will yield the MVUE
      • Find any unbiased estimator $\bar\theta$ for $\theta$, and then determine
        $\hat \theta=E[\bar\theta|T(x)]$
      • This is usually very tedious/difficult to do
      • The expectation is taken over the distribution $p(\bar\theta|T(x))$

Sufficient Statistics

• Example : Estimating a DC Level in WGN
  • $\hat A = \frac{1}{N}\sum_{n=0}^{N-1}x[n]$ : MVUE with variance $\frac{\sigma^2}{N}$
  • $\check{A}=x[0]$ : unbiased estimator with variance $\sigma^2$
    $\check A$ disarded the data points $\{x[1],\cdots,x[N-1]\}$ which carry information about $A$
• Is there a set of data that is sufficient?
  • $S_1=\{x[0],\cdots,x[N-1]\}$ : sufficient statistic
    (Original data set is always sufficient)
  • $S_2=\{x[0]+x[1],\cdots,x[N-1]\}$ : sufficient statistic
  • $S_3=\{\sum_{n=0}^{N-1}x[n]\}$ : minimal sufficient statistis (least # of elements)
• For estimation of $A$, once we know $\sum_{n=0}^{N-1}x[n]$, we no longer need the individual data values

  Since all information has been summarized in the sufficient statistic

• A statistic is the result of applying a function to a set of data - our observations
• A single statistic is a single function of the observations, $T(x)$
• And it is called sufficient statistics if the PDF $p(\text{x}|T(\text{x})=T_0;\theta)$ is independent of $\theta$

---

• Example : Estimating a DC Level in WGN
  $p(\mathbf{x}; A) = \frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}} \exp\left[ -\frac{1}{2\sigma^2} \sum_{n=0}^{N-1} (x[n] - A)^2 \right]\\[0.3cm] T(\mathbf{x}) = \sum_{n=0}^{N-1} x[n] = T_0 \text{ observed}$
• Conditional PDF $p(\text{x}|\sum_{n=0}^{N-1} x[n]=T_0;A)$ should not depend on $A$
  
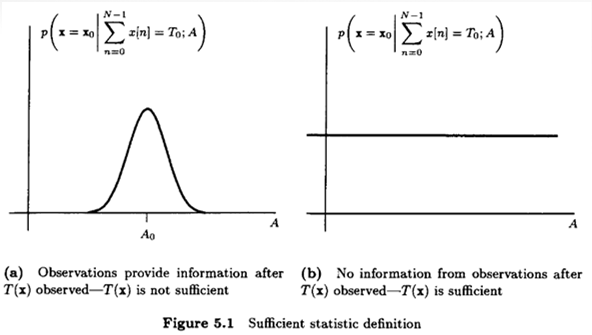
• Verification of a sufficient statistic
  $p(\mathbf{x} | T(\mathbf{x}) = T_0; A) = \frac{p(\mathbf{x}, T(\mathbf{x}) = T_0; A)}{p(T(\mathbf{x}) = T_0; A)}\\[0.3cm] p(T(\mathbf{x}) = T_0; A) = \frac{1}{\sqrt{2\pi N\sigma^2}} \exp\left( -\frac{1}{2N\sigma^2} (T_0 - NA)^2 \right) \\[0.3cm] p(T(\mathbf{x}) \sim \mathcal{N}(NA, N\sigma^2))\\[0.5cm] p(\mathbf{x}; A) \delta(T(\mathbf{x}) - T_0) = \frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}} \exp\left[ -\frac{1}{2\sigma^2} \sum_{n=0}^{N-1} (x[n] - A)^2 \right] \delta(T(\mathbf{x}) - T_0)\\[0.3cm] = \frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}} \exp \left[ -\frac{1}{2\sigma^2} \left(\left( \sum_{n=0}^{N-1} x^2[n]\right) - 2AT(\mathbf{x}) + NA^2 \right) \right] \delta(T(\mathbf{x}) - T_0)\\[0.3cm] = \frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}} \exp \left[ -\frac{1}{2\sigma^2} \left( \left(\sum_{n=0}^{N-1} x^2[n]\right) - 2AT_0 + NA^2 \right) \right] \delta(T(\mathbf{x}) - T_0)$
  Then,
  $p(\mathbf{x} | T(\mathbf{x}) = T_0; A) \\[0.3cm] =\frac{\frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}} \exp\left[ -\frac{1}{2\sigma^2} \sum_{n=0}^{N-1} x^2[n] \right] \exp\left[ -\frac{1}{2\sigma^2} (-2AT_0 + NA^2) \right] }{\frac{1}{\sqrt{2\pi N \sigma^2}} \exp\left[-\frac{1}{2N\sigma^2} (T_0 - NA)^2 \right]}\delta(T(\mathbf{x}) - T_0)\\[0.3cm] = \frac{\sqrt{N}}{(2\pi\sigma^2)^{\frac{N-1}{2}}} \exp\left[ -\frac{1}{2\sigma^2} \sum_{n=0}^{N-1} x^2[n] \right] \exp\left[ \frac{T_0^2}{2N\sigma^2} \right] \delta(T(\mathbf{x}) - T_0)\\[0.4cm] \exp\left[-\frac{1}{2N\sigma^2} (T_0 - NA)^2 \right]=\exp\left[ -\frac{T_0^2}{2N\sigma^2} + \frac{NA T_0}{N\sigma^2} - \frac{NA^2}{2N\sigma^2} \right]\\[0.3cm]=\exp\left[\frac{T_0^2}{2N\sigma^2}\right]$

  Independent of the parameter $A$
  → $T(x)=\sum_{n=0}^{N-1}x[n]$ is sufficient statistic for the estimation of $A$

---

• Evaluation of the conditional PDF is difficult
• Guessing a potential sufficient statistics is even more difficult
• General framework to find sufficient statistic : Neyman-Fisher facorization

---

Neyman-Fisher Factorization

• If we can factor the PDF $p(\text{x};\theta)$ as
  $p(\text{x};\theta)=g(T(\text{x}),\theta)h(\text{x})$
  where $g(\cdot)$ is a function depending on $\text{x}$ only through $T(\text{x})$ and $h(\cdot)$ is a function
  depending only on $\text{x}$
• Then $T(\text{x})$ is a sufficient statistic for $\theta$
• Conversely, if $T(\text{x})$ is a sufficient statistic for $\theta$, then the PDF can be factored as in the above equation
• Proof : Appendix 5A

---

Example 1

• Example : Estimating a DC Level in WGN
  $p(\mathbf{x}; A) = \frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}} \exp\left[ -\frac{1}{2\sigma^2} \sum_{n=0}^{N-1} (x[n] - A)^2 \right]\\[0.3cm] = \frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}} \exp\left[ -\frac{1}{2\sigma^2} \left( \sum_{n=0}^{N-1} x^2[n] - 2A \sum_{n=0}^{N-1} x[n] + NA^2 \right) \right]\\[0.3cm] =g(T(\text{x});A)h(\text{x})\\[0.4cm] \Rightarrow g(T(\mathbf{x}), A) = \frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}} \exp\left[ -\frac{1}{2\sigma^2} \left( -2A \sum_{n=0}^{N-1} x[n] + NA^2 \right) \right],\\[0.3cm]\quad h(\mathbf{x}) = \exp\left[ -\frac{1}{2\sigma^2} \sum_{n=0}^{N-1} x^2[n] \right]\\[0.3cm] \therefore T(\mathbf{x}) = \sum_{n=0}^{N-1} x[n] \text{ is a sufficient statistic for } A$
• Note that any one-to-one function of $T(\text{x})$ is a sufficient statistic

Example 2

• Example : Power of WGN
  $A=0,\;\sigma^2$ is the unknown parameter
  $p(\mathbf{x}; \sigma^2) = \frac{1}{(2\pi\sigma^2)^{\frac{N}{2}}} \exp\left[ -\frac{1}{2\sigma^2} \sum_{n=0}^{N-1} x^2[n] \right]\\[0.3cm] = g(T(\mathbf{x}), \sigma^2) \cdot h(\mathbf{x})\\[0.4cm] T(\mathbf{x}) = \sum_{n=0}^{N-1} x^2[n]$

---

Naturally Extended Neyman-Fisher Factorization

• The $r$ statistics $T_1(\text{x}),T_2(\text{x}),\cdots,T_r(\text{x})$ are joint sufficient statistics
  if the conditional pdf $p(\text{x}|T_1(\text{x}),T_2(\text{x}),\cdots,T_r(\text{x});\theta)$ does not depend on $\theta$
• They are joint sufficient statistics if and only if the pdf may be factored as
  $p(\text{x};\theta)=g(T_1(\text{x}),T_2(\text{x}),\cdots,T_r(\text{x}),\theta)h(\text{x})$
• The original data $\text{x}$ are always sufficient statistics
  $g(T_1(\text{x}),T_2(\text{x}),\cdots,T_r(\text{x}),\theta)=p(x;\theta),\quad h(\text{x})=1$

Phase Examples

• $A, f_0, \sigma^2 : \text{known}$
• $w[n] : \text{WGN}$
• $\phi : \text{Unknown}$
• The exponent may be expanded as
  $\sum_{n=0}^{N-1} x^2[n] - 2A \sum_{n=0}^{N-1} x[n] \cos(2\pi f_0 n + \phi) + \sum_{n=0}^{N-1} A^2 \cos^2(2\pi f_0 n + \phi)\\[0.3cm] = \sum_{n=0}^{N-1} x^2[n] - 2A \left( \sum_{n=0}^{N-1} x[n] \cos 2\pi f_0 n \right) \cos \phi \\[0.3cm]+ 2A \left( \sum_{n=0}^{N-1} x[n] \sin 2\pi f_0 n \right) \sin \phi + \sum_{n=0}^{N-1} A^2 \cos^2(2\pi f_0 n + \phi)$
• No single sufficient statistic exists, but jointly sufficient statistics exist
  $g(T_1(\text{x}),T_2(\text{x}),\phi)\\[0.3cm] p(\mathbf{x}; \phi) = \exp\left( -\frac{1}{2\sigma^2} \left[ \sum_{n=0}^{N-1} A^2 \cos^2(2\pi f_0 n + \phi) - 2A T_1(\mathbf{x}) \cos \phi + 2A T_2(\mathbf{x}) \sin \phi \right] \right)\\[0.3cm] \cdot \frac{1}{(2\pi \sigma^2)^{\frac{N}{2}}} \exp\left( -\frac{1}{2\sigma^2} \sum_{n=0}^{N-1} x^2[n] \right) = h(\mathbf{x})\\[0.4cm] T_1(\mathbf{x}) = \sum_{n=0}^{N-1} x[n] \cos 2\pi f_0 n, \quad T_2(\mathbf{x}) = \sum_{n=0}^{N-1} x[n] \sin 2\pi f_0 n$

Sufficient Statistics and MVUEs

• If we determined a sufficient statistic $T(\text{x})$ for $\theta$

• Then we can use this to improve any unbiased estimator of $\theta$

• As is proven in the Rao-Blackwell-Lehmann-Scheffe(RBLS) theorem

• If we're lucky and the statistic is also complete, we can use it to find the MVUE

  • There are many definitions for the completeness of a statistic
    One that is easy for us to use in the context of estimation is the following :

    It is called complete if only 1 function of it yields an unbiased estimator of $\theta$
    $g(T(\text{x})) :\text{ only one unbiased function}$

    • This is generally difficult to check but is easy conceptually

  • Another way of checking if a statistic is complete :

  $\int_{-\infty}^{\infty} v(T) p(T; \theta) \, dT = 0$

  • A statistic $T$ is complete it contains above for all $\theta$ is only
    satisfied by $v(\text{T}) =0$ for all $T$

Example : DC Level in WGN

• Suppose we don't know that the sample mean is MVUE, but know that
  $T(\text{x})=\sum_{n=0}^{N-1}x[n]$
  is a sufficient statistic
• Two ways to find the MVUE :
  • Find any unbiased estimator of $A$, say $\check A = x[0]$, and determine $\hat A = E(\check A|T)$
    The expectation is taken with respect to $p(\check A|T)$
  • Find some function $g$ so that $\hat A = g(T)$ is an unbiased estimator of $A$

First Approach to find

• For jointly Gaussian random variables $x$ and $y$
  $E(x|y)=E(x)+\frac{\text{cov}(x,y)}{\text{var}(y)}(y-E(y))$
  (Appendix 10A)
  $\begin{bmatrix} x \\ y \end{bmatrix} = \sum_{n=0}^{N-1} x[n] = \begin{bmatrix} 1 & 0 & 0 & \dots & 0 \\ 1 & 1 & 1 & \dots & 1 \end{bmatrix} \begin{bmatrix} x[0] \\ x[1] \\ \vdots \\ x[N-1] \end{bmatrix} = Lx \sim \mathcal{N}(\mu, C)\\[0.5cm]L = \begin{bmatrix} 1 & 0 & 0 & \dots & 0 \\ 1 & 1 & 1 & \dots & 1 \end{bmatrix}\\[0.3cm] \mu = L E(x) = \begin{bmatrix} A \\ NA \end{bmatrix}, \quad C = \sigma^2 L L^T = \sigma^2 \begin{bmatrix} 1 & 1 \\ 1 & N \end{bmatrix}\\[0.3cm] \Rightarrow \hat{A} = E(x | y) = A + \frac{\sigma^2}{N\sigma^2} \left( \sum_{n=0}^{N-1} x[n] - NA \right) = \frac{1}{N} \sum_{n=0}^{N-1} x[n]$

Second Approach

• $E[\hat A]=A$
• $E[T] = NA$
• For unbiased
  $g(x)=\frac{x}{N} \rightarrow \hat A=\frac{1}{N}\sum_{n=0}^{N-1}x[n]$

Rao-Blackwell-Lehmann-Scheffe(RBLS) Theorem

• If $\check \theta$ is an unbiased estimator of $\theta$ and $T(\text{x})$ is a sufficient statistic for $\theta$,
  Then $\hat\theta = E[\check\theta|T(\text{x})]$
  1. A valid estimator for $\theta$ (not dependent on $\theta$)
  2. Unbiased
  3. Of lesser or equal variance thant that of $\check \theta$, for all $\theta$
     
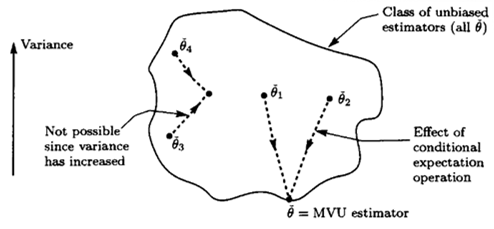
• Additionally, if the sufficient statistic is complete, then $\hat \theta$ is the MVUE
• A statistic is complete if there is only one function of the statistic that is unbiased
  $\hat{\theta} = E(\tilde{\theta} | T(\mathbf{x})) = \int \tilde{\theta}(\mathbf{x}) p(\mathbf{x} | T(\mathbf{x}); \theta) d\mathbf{x} \quad \Rightarrow \text{not depend on } \theta \Rightarrow \text{valid estimator}$
• $p(\text{x}|T(\text{x});\theta)$ doesn't depend on $\theta$ by the definition of sufficient statistic
  $\rightarrow$ 1 is proven
  $E(\hat{\theta}) = \int \int \tilde{\theta}(\mathbf{x}) p(\mathbf{x} | T(\mathbf{x}); \theta) d\mathbf{x} p(T(\mathbf{x}); \theta) dT\\[0.3cm] = \int \tilde{\theta}(\mathbf{x}) \left( \int p(\mathbf{x} | T(\mathbf{x}); \theta) p(T(\mathbf{x}); \theta) dT \right) d\mathbf{x}\\[0.3cm] = \int \tilde{\theta}(\mathbf{x}) p(\mathbf{x}; \theta) d\mathbf{x} = E(\tilde{\theta}) = \theta \quad \Rightarrow \text{unbiased (2 is proven)}$
  $\text{var}(\check{\theta}) = E\left[ \left( \check{\theta} - E(\check{\theta}) \right)^2 \right] = E\left[ \left( \check{\theta} - \hat{\theta} + \hat{\theta} - \theta \right)^2 \right]\\[0.3cm] = E\left[ (\check{\theta} - \hat{\theta})^2 \right] + 2E\left[ (\check{\theta} - \hat{\theta})(\hat{\theta} - \theta) \right] + E\left[ (\hat{\theta} - \theta)^2 \right]\\[0.3cm] \text{var}(\hat\theta)=E\left[(\hat\theta-\theta)^2\right]$
• Note that $E\left[ (\tilde{\theta} - \hat{\theta})(\hat{\theta} - \theta) \right] = 0$ since
  $E_{T,\check\theta}\left[(\check\theta-\hat\theta)(\hat\theta-\theta)\right]=E_TE_{\check\theta|T}\left[(\check\theta-\hat\theta)(\hat\theta-\theta)\right]\\[0.3cm] =E_T\left[E_{\check\theta|T}\left[(\check\theta-\hat\theta)(\hat\theta-\theta)\right]\right]=E_T\left[(E_{\check\theta|T}\left[\check\theta\right]-\hat\theta)(\hat\theta-\theta)\right]\\[0.3cm] E_T\left[(\hat\theta-\hat\theta)(\hat\theta-\theta)\right] =0$
• Thus, $\text{var}(\check\theta)=E\left[(\check\theta-\hat\theta)^2\right] + \text{var}(\hat\theta) \geq\text{var}(\hat\theta)$ : 3 is proven

---

• If $T(\text{x})$ is complete, there is only one function of $T$ that is an unbiased estimator
  • $\hat\theta$ is unique independent of $\hat\theta$
  • $\text{var}(\hat\theta)\leq\text{var}(\check\theta)$ for all $\check\theta$
  • $\hat\theta$ must be an MVUE
• Completeness depends on the PDF of $\text{x}$
• This condition is satisfied for the exponential family of PDFs

RBLS Example

• Incomplete sufficient statistic
  $x[0]=A+w[0],\quad w\sim U\left[-\frac{1}{2},\frac{1}{2}\right]$
• $E[x[0]]=A+E[w[0]]=A$
• $x[0]$ is sufficient statistic and an unbiased estimator

  Is $g(x[0])=x[0]$ a MVUE?

  • Suppose that there exists another function $h$ w/ the unbiased property
    $E[h(x[0])] =A$ and see if $h=g$
  • Let $v(T)=g(T)-h(T)$, then $\int_{-\infty}^{\infty} v(T) p(\mathbf{x}; A) d\mathbf{x} = 0$ for all $A$
  • Since $\text{x}=x[0]=T,\;\int_{-\infty}^{\infty} v(T) p(T; A) dT = 0$ for all $A$
    $p(T; A) = \begin{cases} 1, & A - \frac{1}{2} \leq T \leq A + \frac{1}{2} \\ 0, & \text{otherwise} \end{cases} \quad \Rightarrow \int_{A-\frac{1}{2}}^{A+\frac{1}{2}} v(T) dT = 0 \text{ for all } A$
  • $v(T) =\sin2\pi T$ satisfies the condition
    ⇒ $\hat A=x[0]-\sin2\pi x[0]$ based on the sufficient statistic and is unbiased → No
• Completeness condition is that only the zero function $v(T)=0$ satisfies
  $\int_{-\infty}^{\infty} v(T) p(T; A) dT = 0$

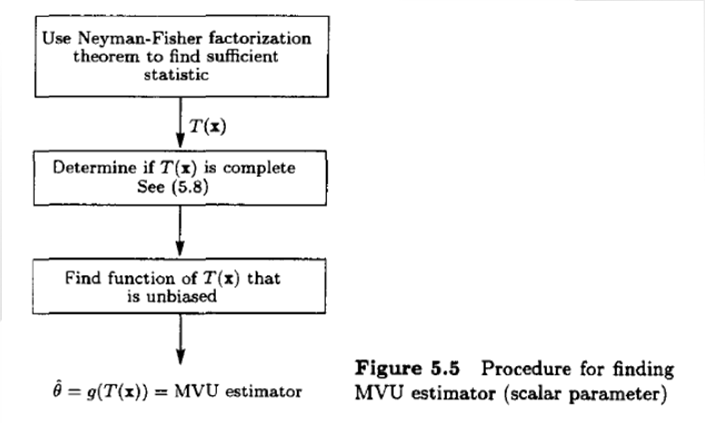
  Procedure for finding MVUE(Scalar)

  1. Use Neyman-Fisher Factorization to find sufficient statistic $T(\text{x})$
  2. Determine if $T(\text{x})$ is complete;
     The condition for completeness is that only the zero function
     $v(T)=0$ satisfies $\int_{-\infty}^{\infty} v(T) p(T; \theta) dT = 0$ for all $\theta$
  3. Find a function $g$ of $T(\text{x})$ that is unbiased
     Then $\hat \theta = g(T(\text{x}))$ is the MVUE
     Or alternatively, evaluate $\hat\theta=E\left[\check\theta|T(\text{x})\right]$ where $\check\theta$ is any unbiased estimator
     

Example : Mean of Uniform Noise

• Consider estimating the mean $\theta = \beta/2$ of the i.i.d. uniform noise
  $w[n]\sim U[0,\beta]$
• $x[n]=w[n],\quad n=0,1,\cdots,N-1$
• Find an efficient estimator
  • The regularity condition does not hold : CRLB cannot be applied
  • Natural guess : sample mean estimator
    $\hat \theta =\frac{1}{N}\sum_{n=0}^{N-1} x[n]\rightarrow\text{unbiased}\\[0.3cm] \text{var}(\hat\theta)=\frac{1}{N^2}\cdot N\cdot\text{var}(x[n])=\frac{1}{N}\text{var}(x[n])=\frac{\beta^2}{12N}$
  • Is the sample mean estimator MVUE?
• Follow Figure 5.5 unit step function
  $p(x[n]; \beta) = \frac{1}{\beta} [u(x[n]) - u(x[n] - \beta)], \quad u(x): \text{unit step function}\\[0.3cm] p(x; \beta) = \frac{1}{\beta^N} \prod_{n=0}^{N-1} [u(x[n]) - u(x[n] - \beta)]\\[0.3cm] p(x; \beta) = \begin{cases} \frac{1}{\beta^N}, & \max x[n] < \beta, \min x[n] > 0 \\ 0, & \text{otherwise} \end{cases}\\[0.3cm] \Rightarrow p(x; \beta) = \frac{1}{\beta^N} u(\beta - \max x[n]) u(\min x[n])\\[0.3cm] \Rightarrow T(x) = \max x[n]$
• $T(\text{x})$ : sufficient statistic for $\theta$, and also complete
• Next, we need to find a function $g$ of $T(\text{x})$ that is unbiased
  $p_{x[n]}(\xi; \beta) = \begin{cases} \frac{1}{\beta}, & 0 < \xi < \beta \\ 0, & \text{otherwise} \end{cases} \quad \text{PDF of } x[n]\\[0.3cm] \text{CDF: } \Pr\{x[n] \leq \xi\} = \begin{cases} 0, & \xi < 0 \\ \frac{\xi}{\beta}, & 0 < \xi < \beta \\ 1, & \xi \geq \beta \end{cases}\\[0.3cm] \Pr\{T \leq \xi\} = \prod_{n=0}^{N-1} \Pr\{x[n] \leq \xi\} = \Pr\{x[n] \leq \xi\}^N : \text{CDF of } T(x)\\[0.3cm] p_T(\xi) = \begin{cases} 0, & \xi < 0 \\ N \left(\frac{\xi}{\beta}\right)^{N-1} \frac{1}{\beta}, & 0 < \xi < \beta \\ 0, & \xi > \beta \end{cases} \quad \text{PDF of } T(x)\\[0.3cm] E(T) = \int_{-\infty}^{\infty} \xi p_T(\xi) d\xi = \int_0^{\beta} \xi N \left(\frac{\xi}{\beta}\right)^{N-1} \frac{1}{\beta} d\xi = \frac{N}{N+1} \beta = \frac{2N}{N+1} \theta$
• To make this unbiased
  $\hat\theta=\frac{N+1}{2N}\max x[n]:\text{MVUE}$
  $\therefore$ The sample mean estimator was not the MVUE
  $\text{var}(\hat{\theta}) = \left( \frac{N+1}{2N} \right)^2 \text{var}(T)\\[0.3cm] \text{var}(T) = \left( \frac{N+1}{2N} \right)^2 \left( \int_{-\infty}^{\infty} \xi^2 p_T(\xi) d\xi - \left( \frac{N\beta}{N+1} \right)^2 \right)\\[0.3cm] = \left( \frac{N+1}{2N} \right)^2 \left( \frac{N\beta^2}{(N+1)^2 (N+2)} \right) = \frac{\beta^2}{4N(N+2)}\leq\frac{\beta^2}{12N}$
• Smaller than the variance of sample mean estimator for $N\geq2$
• Not easy to apply when there is no single sufficient statistic

Extensions to Vector Parameters

• If we can factor the PDF $p(x;\theta)$ as
  $p(\text{x};\theta)=g(T(\text{x}),\theta)h(\text{x})$
• $g$ is a function depending on $\text{x}$ only through $T(\text{x})$, an $r\times 1$ statistic
• And $h$ is function depending on $\text{x}$
• Then $T(\text{x})$ is a sufficient statistic for $\theta$
• Conversely, if $T(\text{x})$ is a sufficient statistic for $\theta$, then the PDF can be factored as above
• Sufficiency :$T(\text{x})=[T_1(\text{x})\cdots T_r(\text{x})]^T$ is sufficient for the estimation of $\theta$ if
  $p(\text{x}|T(\text{x});\theta)=p(\text{x}|T(\text{x}))$

RBLS

• If $\check\theta$ is an unbiased estimator of $\theta$ and $T(\text{x})$ is an $r\times 1$ sufficient statistic for $\theta$
  Then $\hat \theta = E[\check \theta|T(\text{x})]$ is
  1. A valid estimator for $\theta$ ( not dependent on $\theta$)
  2. Unbiased
  3. Of lesser or equal variance than that of $\check\theta$ (each element of $\hat\theta$ has less or equal variance)
• Additionally, if the sufficient statistic is complete
  then $\hat\theta$ is the MVUE
  • Completeness : if for $v(T)$, an arbitrary $r\times1$ function of $T$
  • $E(v(T)) = \int_{-\infty}^{\infty} v(T) p(T; \theta) dT = 0$ for all $\theta$, then $v(T) =0$ for all $T$

All Content has been written based on lecture of Prof. eui-seok.Hwang in GIST(Detection and Estimation)