Introduction
- Up to now -
Classical Approach: the parameter is adeterministicbutunknown constant- Assumes is deterministic
- Variance of the estimate could depend on
- In Monte Carlo simulations:
- runs done at the same , must do runs at each of interest
- Averaging done over data, No averaging over values
- From now on -
BayesianApproach : the parameter is a random variable whose particular realization we must estimate- Assumes is
randomwith pdf - Variance of the estimate
CAN'Tdepend on - In Monte Carlo simulations
- Each run done at a randomly chosen
- Averaging done over data
ANDover values
- Assumes is
Motivation
- Sometimes we have
prior knowledgeon some values are more likely than others - Useful when the
classicalMVUE does not exist because of non-uniformity of minimal variance →optimal on the average

To combat thesignal estimation problemestimate signalClassicalsolution :Bayesiansolution : the Wiener filter
Prior Knowledge and Estimation
- The use of
prior knowledgewill lead to a more accurate estimator Ex)DC Level in WGN- :
MVUE, but can beoutside of the range 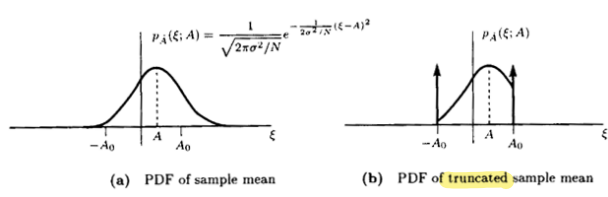
- :
Mean squared error(MSE)- The
truncated sample mean estimatoris better than thesample mean estimator(MVUE) in terms of MSE - Using prior knowledge, is assumed to be a random variable,
→ The problem is to estimate the value of or the realization of
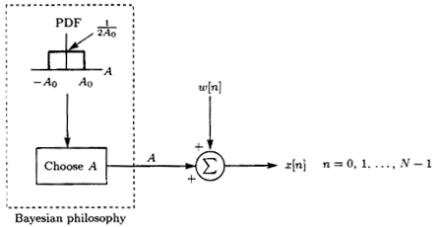
- The
Bayesian MMSE Estimation
Bayesian MSE(Bmse)Bmseis minimized if isminimizedfor each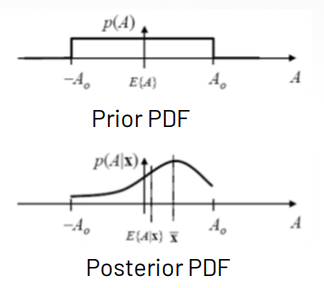
Ex)DC Level in WGN
- is a function of
- MMSE estimator of before observing
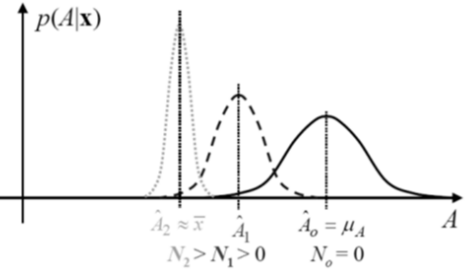
- The posterior mean lies between and
- As
- In general,
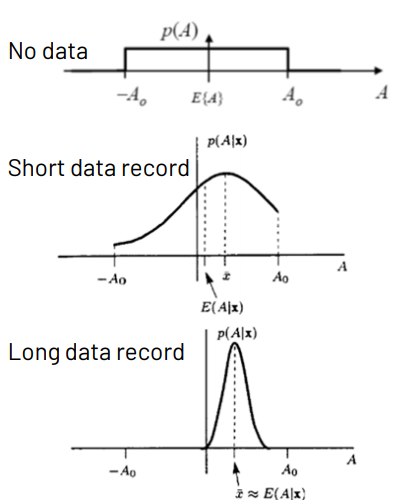
Choosing a Prior PDF
- Once a prior PDF has been chosen, the MMSE is: usually difficult to obtain closed-form solution(numerical integration is needed
- Choice is crucial :
- Must be able to justify it physically
- Anything other than a
Gaussian priorwill likely result in no closed-form estimates
(previous example showed a uniform prior led to a non-closed form,
later exqmple shows a Gaussian prior gives a closed form) - There seems to be a trade-off between
- choosing the prior PDF as accurately as possible
- choosing the prior PDF to give computable closed form
Gaussian Prior PDF Example
Ex)DC Level in WGN - Gaussian Prior PDF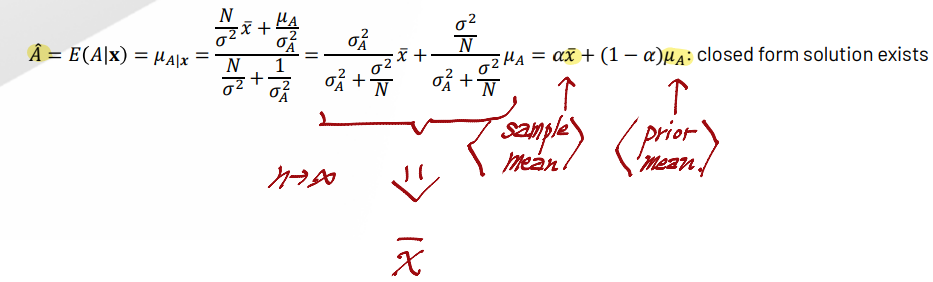
- As
improved performance with prior knowledge
-
Gaussian→Gaussian: reproducing property
→ Only mean and variance are recomputed
- Note
Closed-FormSolution for Estimate!- Estimate is weighted sum of prior mean & data mean
- Weights balance between prior info quality and data quality
- As increases...
- Estimate moves
- Accuracy moves
Gaussian Dat & Gaussian Prior gives Closed-Form MMSE Solution
Bivariate Gaussian PDF
- If and are distributed according to a bivariate Gaussian PDF with
mean vector , covariance matrix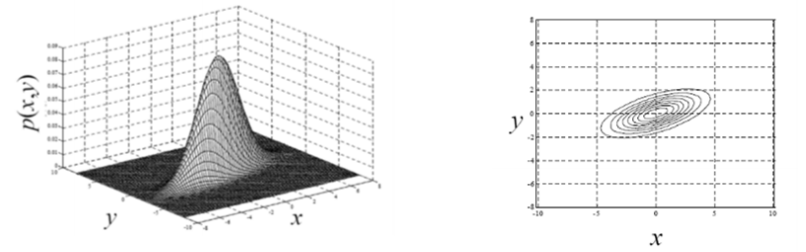
- The marginal (or individual) PDFs by integrating:
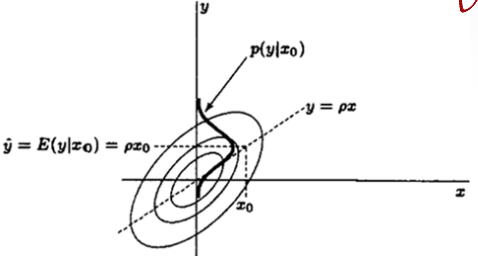
- The conditional PDF is also Gaussian and
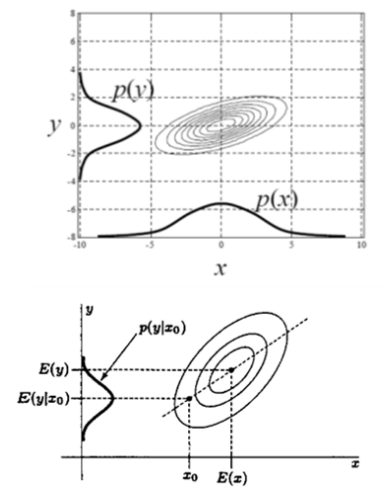
- Prior PDF :
After observing , the posterior PDFIf is large then, variance reduction become larger
Multivariate Gaussian PDF
- Let and are jointly Gaussian with andso thatThen, is also Gaussian and,
