정책반복과 가치반복

앞서 진행했던 부분은 미로 안을 무작위로 이동하는 정책을 구현했다. 이번에는 에이전트가 목표로 곧장 향하도록 정책을 학습해야 하는데 크게 두 가지 방법으로 나뉜다.

1. 목표에 빠르게 도달했던 경우에 수행했던 행동(action)
   이때의 행동을 앞으로도 취할 수 있도록 정책을 수정하는 방법
2. 목표지점부터 거슬러 올라가며 목표 지점과 가까운 상태 로 에이전트를 유도
   목표 지점 외의 지점에도 가치(우선도)를 부여

첫번째를 정책반복, 두번째를 가치반복이라고 한다

정책경사(Policy gradient) 알고리즘

• 정책 파라미터 $\theta$에서 정책 $\pi_\theta(s,a)$를 구하는 방법으로 앞선 부분에서는 함수를 구현했지만 이번에는 Softmax 함수를 사용할 것이다

• Softmax

  $p(\theta_i)=\frac{\exp(\beta\theta_i)}{\exp(\beta\theta_1)+\exp(\beta\theta_2)+\cdots}\\[0.3cm] =\frac{\exp(\beta\theta_i)}{\sum_{j=1}^{N_a}\exp(\beta\theta_j)}$

• $N_a$ : 선택 가능한 행동의 가짓수, 미로 태스크의 경우 상하좌우 4방향이므로 4

• $\beta$ : 역온도(inverse temperature) 작아질수록 행동이 무작위로 선택된다

정책경사 구현

# 정책 파라미터 theta를 행동정책 pi로 변환(소프트맥스 함수 사용)하는 함수

def softmax_convert_info_pi_from_theta(theta):
    '''비율 계산에 소프트맥스 함수 사용'''
    beta = 1.0
    [m, n] = theta.shape # theta 행렬의 크기를 구함
    pi = np.zeros((m, n))

    exp_theta = np.exp(beta * theta) # theta를 exp(theta)로 변환

    for i in range(0, m):
        # pi[i, :] = theta[i, :] / np.nansum(theta[i, :])
        # 단순 비율을 계산하는 코드
        pi[i, :] = exp_theta[i, :] / np.nansum(exp_theta[i, :])
        # softmax로 계산하는 코드

    pi = np.nan_to_num(pi) # nan을 0으로 변환

    return pi

• 이어서 softmax_convert_into_pi_from_theta 함수를 사용해 파라미터 $\theta_0$으로부터 정책 $\pi_{\theta_0}(s,a)$를 구한다

# 초기 정책 pi_0을 계산
pi_0 = softmax_convert_info_pi_from_theta(theta_0)
print(pi_0)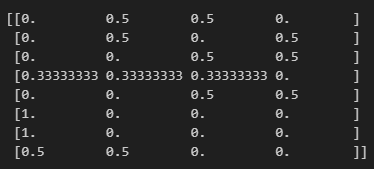

• 이번에는 소프트맥스 함수로 계산한 정책을 적용해 에이전트를 움직이는 함수를 구현한다
  앞서 구현했던 1단계 이동 후의 에이전트 상태를 구하는 함수를 조금 수정한다
  상태 외에 이때 취했던 행동(상, 하, 좌, 우)를 함께 반환하도록 한다

# 행동 a와 1단계 후의 상태 s를 구하는 함수

def get_action_and_next_s(pi, s):
    direction = ["up", "right", "down", "left"]
    # pi[s, :]의 확률에 따라 direction 값이 선택된다
    next_direction = np.random.choice(direction, p=pi[s,:])

    if next_direction == "up":
        action = 0
        s_next = s - 3 #위로 이동하면 상태 값 3 감소
    elif next_direction == "right":
        action = 1
        s_next = s + 1 # 오른쪽으로 이동하면 상태값 1 증가
    elif next_direction == "down" :
        action = 2
        s_next = s + 3 # 아래로 이동하면 상태 3 증가
    elif next_direction == 'left' :
        action = 3
        s_next = s - 1 # 왼쪽으로 이동하면 상태값이 1 줄어듬

    return [action, s_next]

• 그리고 이번에는 상태 외에도 해당 상태에서 취했던 행동에 대한 정보도 모아두도록 수정한다.

# 미로를 빠져나오는 함수, 상태와 행동의 히스토리를 출력한다

def goal_maze_ret_s_a(pi):
    s = 0 # 시작 지점
    s_a_history = [[0, np.nan]] # 에이전트의 행동 및 상태의 히스토리를 기록하는 리스트

    while (1) : # 목표 지점에 이를 때까지 반복
        [action, next_s] = get_action_and_next_s(pi, s)
        s_a_history[-1][1] = action
        # 현재 상태(마지막이므로 인덱스가 -1)를 히스토리에 추가

        s_a_history.append([next_s, np.nan])
        # 다음 상태를 히스토리에 추가, 행동은 아직 알 수 없으므로 nan으로 둔다

        if next_s == 8 : # 목표 지점에 이르면 종료
            break
        else :
            s = next_s

    return s_a_history

• 이제 초기 정책 $\pi_{\theta_0}(s,a)$로 goal_maze_ret_s 함수를 실행

# 초기 정책으로 미로를 빠져나오기
s_a_history = goal_maze_ret_s_a(pi_0)
print(s_a_history)
print("단계 수 "+ str(len(s_a_history) - 1))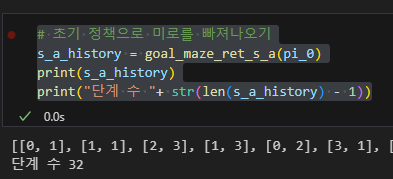

정책경사 알고리즘으로 정책 수정

• $\theta_{s_i,a_j}$는 상태(위치) $s_i$에서 행동 $a_k$를 취할 확률을 결정하는 파라미터이다
• $\eta$ : 학습률, $\theta_{s_i,a_j}$가 1번 학습에 수정되는 정도를 제어
• $N(s_i, a_j)$ : 상태 $s_i$에서 행동 $a_j$를 취했던 횟수
• $P(s_i,a_j)$ : 현재 정책하에서 상태 $s_i$ 일 때 행동 $a_j$를 취할 확률
• $N(s_i,a)$ : 상태 $s_i$에서 행동을 취한 횟수의 합계
• $T$ : 목표 지점에 이르기까지 걸린 모든 단계의 수

# theta를 수정하는 함수

def update_theta(theta, pi, s_a_history):
    eta = 0.1 # 학습률
    T = len(s_a_history) - 1 # 목표 지점에 이르기까지 걸린 단계 수

    [m, n] = theta.shape # theta의 행렬 크기를 구함
    delta_theta = theta.copy() # delta of theta를 구할 준비, 포인터 참조이므로 
                               # delta_theta = theta로는 안 됨

    # delta_theta를 요소 단위로 계산
    for i in range(0, m):
        for j in range(0, n):
            if not(np.isnan(theta[i, j])): # theta가 nan이 아닌 경우
                SA_i = [SA for SA in s_a_history if SA[0] == i]
                # 히스토리에서 상태 i인 것만 모아오는 리스트 컴프리헨션

                SA_ij = [SA for SA in s_a_history if SA == [i, j]]
                # 상태 i에서 행동 j를 취한 경우만 모음

                N_i = len(SA_i) # 상태 i에서 모든 행동을 취한 횟수
                N_ij = len(SA_ij) # 상태 i에서 행동 j를 취한 횟수

                delta_theta[i, j] = (N_ij - pi[i, j] * N_i) / T

    new_theta = theta + eta * delta_theta

    return new_theta 

• 포인터 참조를 통해 바로 반영하도록 한다

# 정책 수정
new_theta = update_theta(theta_0, pi_0, s_a_history)
pi = softmax_convert_info_pi_from_theta(new_theta)
print(pi)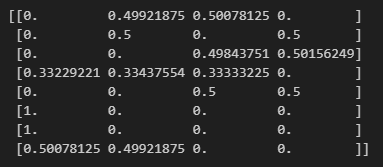

• 처음에 균등분포에 가까웠던 각 행동의 확률이 변화한 것을 알 수 있다

• 이제 미로에서 목표 지점으로 바로 갈 수 있을 만큼 파라미터 $\theta$를 반복해서 수정하도록 하는 가장 바깥쪽 반복문을 마지막으로 구현

# 정책 경사 알고리즘으로 미로 빠져나오기

stop_epsilon = 10**-4

theta = theta_0
pi = pi_0

is_continue = True
count = 1

while is_continue : # is_continue가 False가 될 때까지 반복
    s_a_history = goal_maze_ret_s_a(pi) # 정책 pi를 따라 미로를 탐색한 히스토리를 구함
    new_theta = update_theta(theta, pi, s_a_history) # 파라미터 theta를 수정
    new_pi = softmax_convert_info_pi_from_theta(new_theta) # 정책 pi를 수정

    print(np.sum(np.abs(new_pi - pi))) # 정책의 변화를 출력
    print("총 단계 수 :" + str(len(s_a_history) - 1))

    if np.sum(np.abs(new_pi - pi)) < stop_epsilon:
        is_continue = False
    else :
        theta = new_theta
        pi = new_pi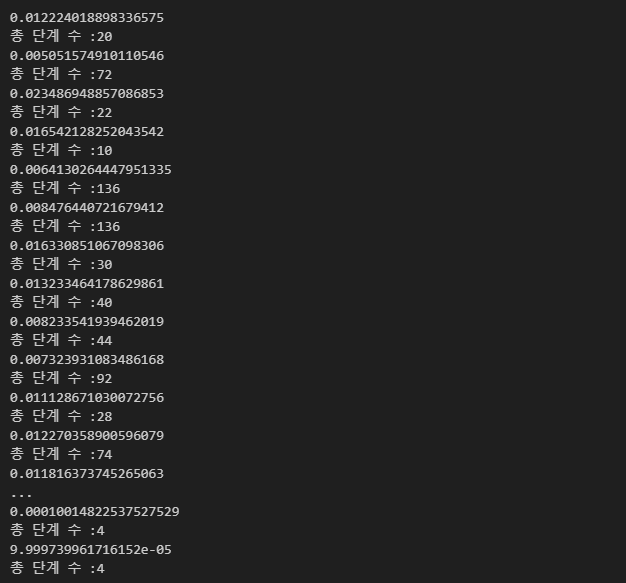

• 정책경사 알고리즘으로 학습한 정책을 확인해 보자

# 학습이 끝난 정책을 확인
np.set_printoptions(precision=3, suppress=True)
# 유료 자릿수 3, 지수는 표시하지 않음
print(pi)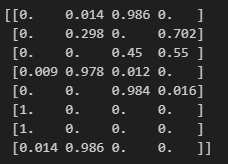

• 애니메이션 구현

from matplotlib import animation
from IPython.display import HTML
import matplotlib.pyplot as plt

# 애니메이션 저장을 위한 Pillow 라이브러리
import matplotlib.pyplot as plt

# 초기화 및 애니메이션 함수
def init():
    # 배경 이미지 초기화
    line.set_data([], [])
    return (line,)

def animate(i):
    # 프레임 단위로 이미지 생성
    state = s_a_history[i][0]  # 현재 위치
    x = (state % 3) + 0.5  # 상태의 x좌표 : 3으로 나눈 나머지 + 0.5
    y = 2.5 - int(state / 3)  # y좌표 : 2.5에서 3으로 나눈 몫을 뺌
    line.set_data(x, y)
    return (line,)

# 애니메이션 생성
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=len(s_a_history), interval=200, repeat=False)

# HTML에서 애니메이션 재생
HTML(anim.to_jshtml())

# 애니메이션을 GIF로 저장
anim.save("animation.gif", writer="pillow", fps=5)  # 파일 이름과 프레임 속도 설정!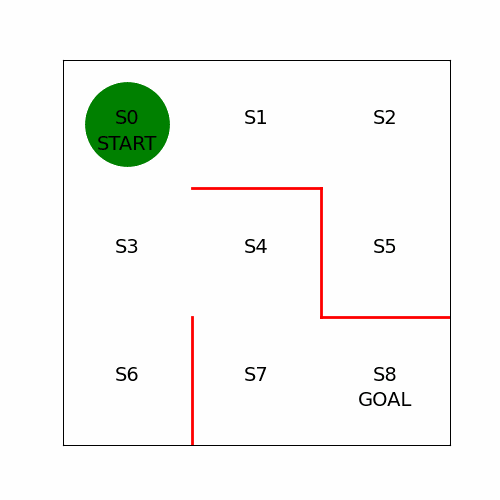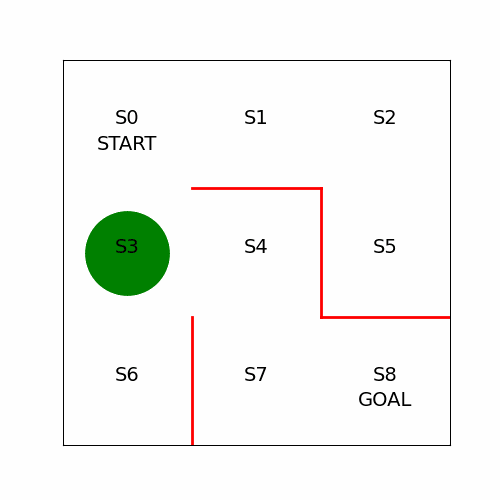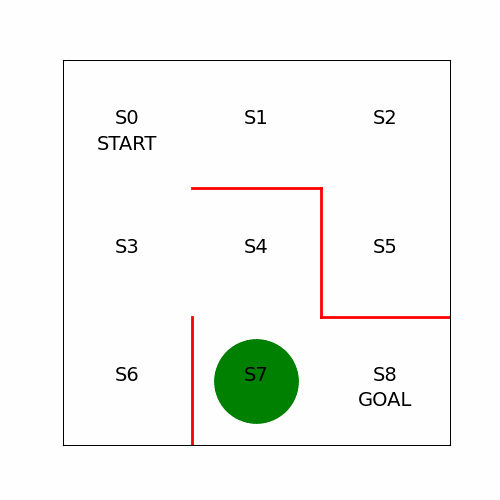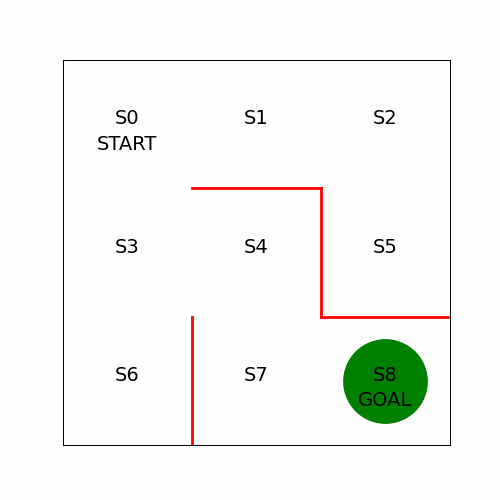

정책경사 알고리즘에 대한 이론

• 왜 정책을 계산할 때 소프트맥스를 사용했는가?
  : 파라미터 $\theta$가 음수가 돼도 정책을 계산할 수 있기 때문 왜냐면 지수함수의 함수값은 항상 양수
• $\theta$를 수정하는 식은 왜 그런 형태여야 하는가?
  : 소프트맥스 함수로 확률을 변환하고 REINFORCE 알고리즘을 사용하면 우리가 $\theta$를 수정하는 식이 유도된다