인공지능을 공부하다 보면 CrossEntropy에 대한 개념을 꼭 공부하게 될 것이다.
본 글에서는 인공지능 개발에 있어서 매우 중요한 개념인 CrossEntropy와 KL divergence에 대해 알아볼 것이다.
정보량
정보이론에서는 정보량을 다음과 같이 표현한다.
그 의미는 '놀랄만한 정도'로 이해할 수 있을 것이다.
일어날 확률이 적은 사건일수록 놀라는 정도가 높다고 이해하면 직관적으로 이해가 쉬울 것이다.
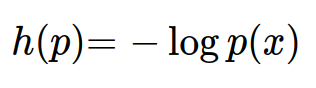
Entropy & Cross Entropy
엔트로피는 정보량의 기댓값으로 정의할 수 있다.
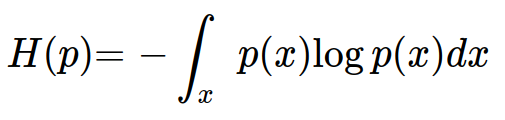
q(x)의 정보량을 p(x)의 분포에 대한 기댓값으로 계산한 결과인 크로스 엔트로피(Cross Entropy)는 다음과 같다.
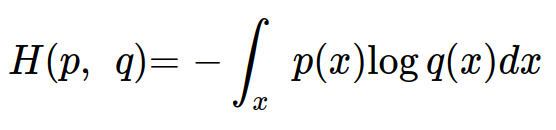
KL Divergence
Cross Entropy는 q(x)의 정보량을 p(x)의 분포에 대한 기댓값을 계산한 결과이지만, KL Divergence는 두 정보량 사이의 상대적인 차이를 계산하는 것이다. 다음과 같이 정의할 수 있다.
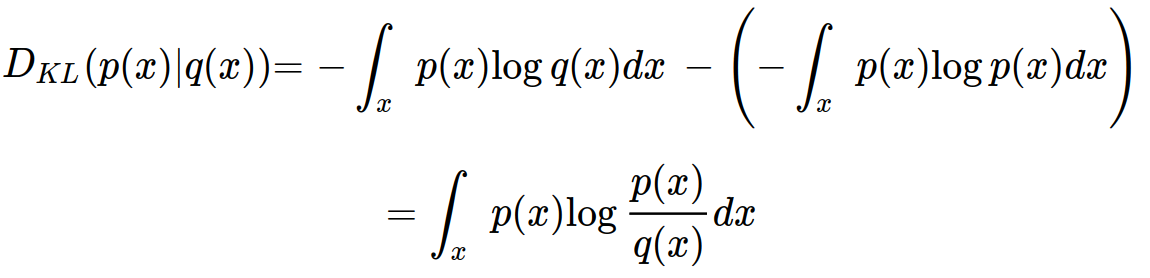
KL divergence는 항상 0보다 크거나 같은 값을 갖게 되는데, 이 성질은 젠센 부등식 (Jensen inequality)를 통해 증명할 수 있다.
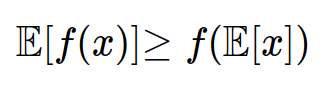
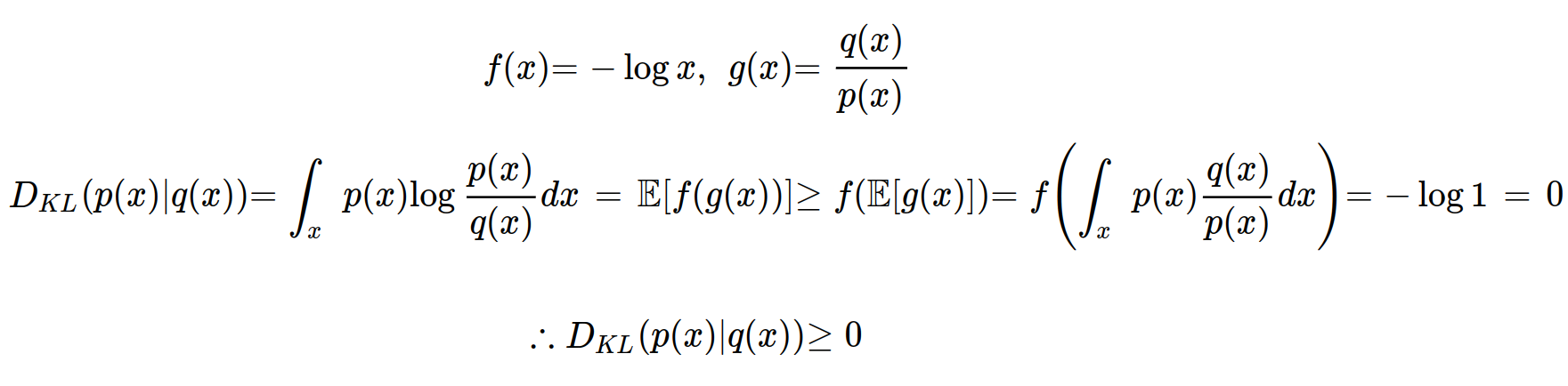
이렇게 KL Divergence는 항상 0보다 크거나 같은 값을 갖게 된다는 성질을 증명할 수 있게 되었다. 살짝 정리하여 다음과 같은 식도 얻을 수 있다.
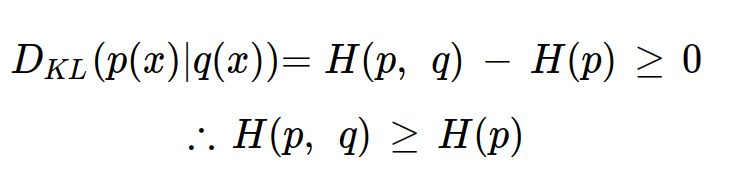
다른 확률밀도함수인 q(x)의 정보량을 확률밀도함수 p(x)의 관점에서 크로스 엔트로피를 구한 값은 p(x)의 엔트로피보다 항상 크거나 같다.
그렇기 때문에 H(p, q)의 값을 최소로 하는 확률밀도함수 q(x)는 p(x)와 같게 된다.
즉, 인공지능을 학습시킬 때 KL Divergence를 사용하나, Cross Entropy를 사용하나 결과적으로는 확률밀도함수 q(x)는 p(x)를 근사하게 되는 것이다.