[실험실] Problem of non zero-centered activation function

문제

cs231n 강의를 듣다가 sigmoid 함수가 zero-centered 하지 않기 때문에 학습에 효과적이지 않다는 얘기를 들었다.

크게 두가지 문제가 있다
1. gradient가 0으로 수렴한다 (이건 뭐 쉽게 이해됐다)
2. 함수의 출력값이 $0<f(x)<1$ 이므로 모든 gradient가 양수가 되어 학습이 단편적인 방향으로 이루어지게 된다.

여기서 엥 했다. 함수의 출력값이랑 기울기랑 뭔 상관이지? gradient가 모두 양수라는걸 잘못 얘기한건가?

사전 조사

사전 조사 내용은 이 그림 하나면 어느정도 요약된다.

activation function 의 출력값이 모두 양수라면, local gradient 또한 모두 양수가 된다.

처음에는 특정 계층의 sigmoid 함수에서 위 두 조건이 성립하게 되는건가 해서 이해가 잘 안됐는데, sigmoid 함수의 출력값이 다음 계층의 입력값이 된다고 생각하니 쉬웠다.

$w$ 의 local gradient 를 대충 구하자면 $x$ 다. 즉, 직전 계층의 출력값이 local gradient가 된다. 그런데 직전 layer의 활성화 함수가 sigmoid라면 모든 local gradient는 0에서 1사이의 양수가 될 수밖에 없다

모든 local gradient가 양수라면, 모든 $w$의 학습 방향이 같아진다.

$dL \over dw$ 는 최종 출력값에 대한 loss 함수의 local gradient에서 시작한다. 편의상 최초의 gradient라고 하자. 이 값이 정해지면 그 뒤로는 모두 똑같다. 역전파가 일어나며 계속 local gradient를 곱해가는데, 존재하는 모든 local gradient가 양수이므로 최초의 gradient의 부호가 모든 $dL \over dw$의 부호가 된다. 듣기만 해도 문제일 것 같은데, 사실 학습은 가능하다. 근데 이제 위 그림에 있는 빨간색 화살표처럼 비효율적일뿐이다. $w$가 업데이트 될 때 당연하게도 특정 $w_1$는 + 되고, 특정 $w_2$는 - 가 되는 것이 더 학습에 유리한 상황이 있을 텐데, sigmoid를 사용할 경우 모든 값의 부호가 통일되므로 비효율적인 학습이 된다.

실험

목표

실제 sigmoid를 사용했을 때 $w$의 부호가 통일되는지 확인하기 위해 간단한 신경망을 생성하고 gradient를 도식화해보자

수식

$w$의 gradient를 구하기 위해 미분해보자. 복잡하니 아래처럼 두개의 수식으로 나눠서 미분하자.

이건 다른 블로그에 잘 정리되어 있다.

사실 수식을 이렇게 써도 되는지 모르겠는데, 일단 써보자
결론적으로 Linear layer와 sigmoid를 사용해서 신경망을 생성한다면 모든 local gradient는 양수가 된다. 앞서 얘기했던 사실이 맞았음을 확인할 수 있다.

v1.0

two-layer NN을 생성하고 가중치를 히스토그램으로 출력하자

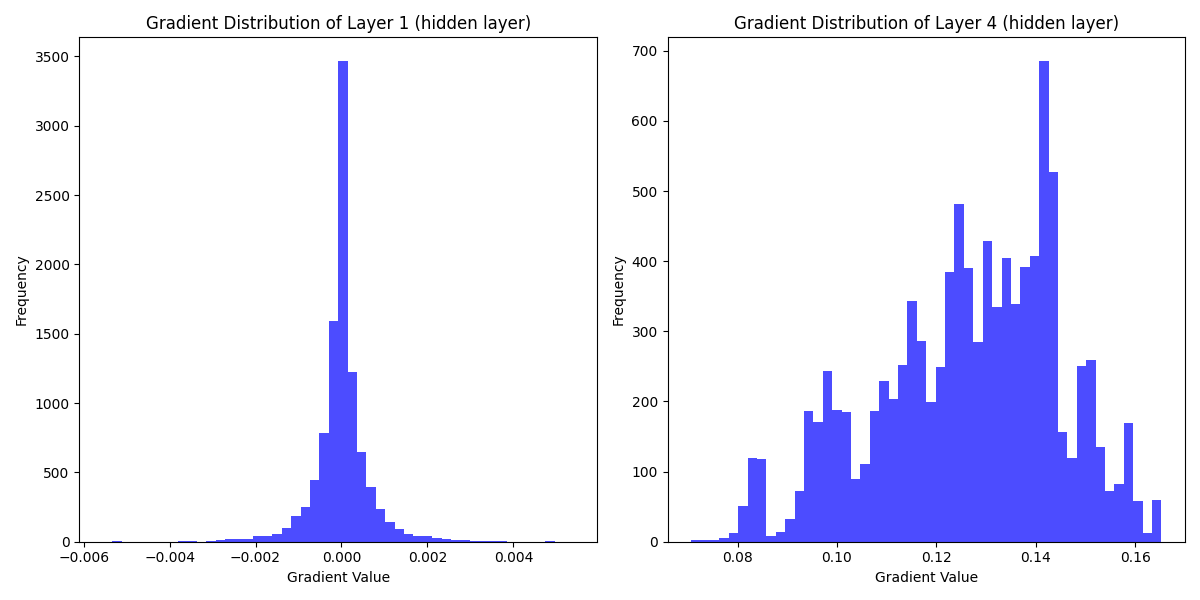
왼쪽 히스토그램은 첫번째 레이어의 가중치이므로 입력값 $x$의 값이 무작위다. 따라서 가중치도 음수, 양수 상관 없이 나온다. 오른쪽 히스토그램은 두번째 레이어이므로 예상대로 모든 gradient가 양수임을 확인할 수 있다.

사실 마지막에 MSE 같은 loss 함수가 아니라 단순히 sum을 해줬다. 신경망으로써 역할은 하지 않지만, 가중치를 확인하는데는 문제가 없다. MSE로 할 경우 음수가 나올 수 있지만 모든 w의 가중치의 부호가 똑같다는 것은 동일하다.

v1.1

Loss function을 MSE로 바꿔보자

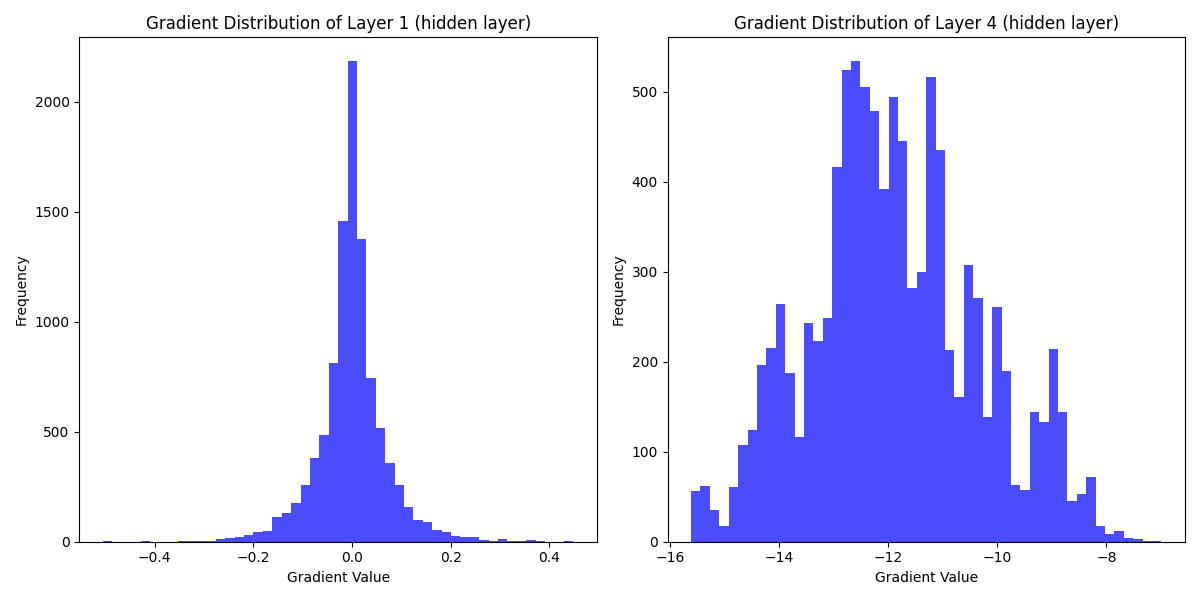
위 사진이 MSE로 loss를 변경하고 다시 출력한 가중치다. 전부 음수인 것을 확인할 수 있다.

v2.0

자신감을 가지고 hidden layer의 수를 조금 늘려봤다

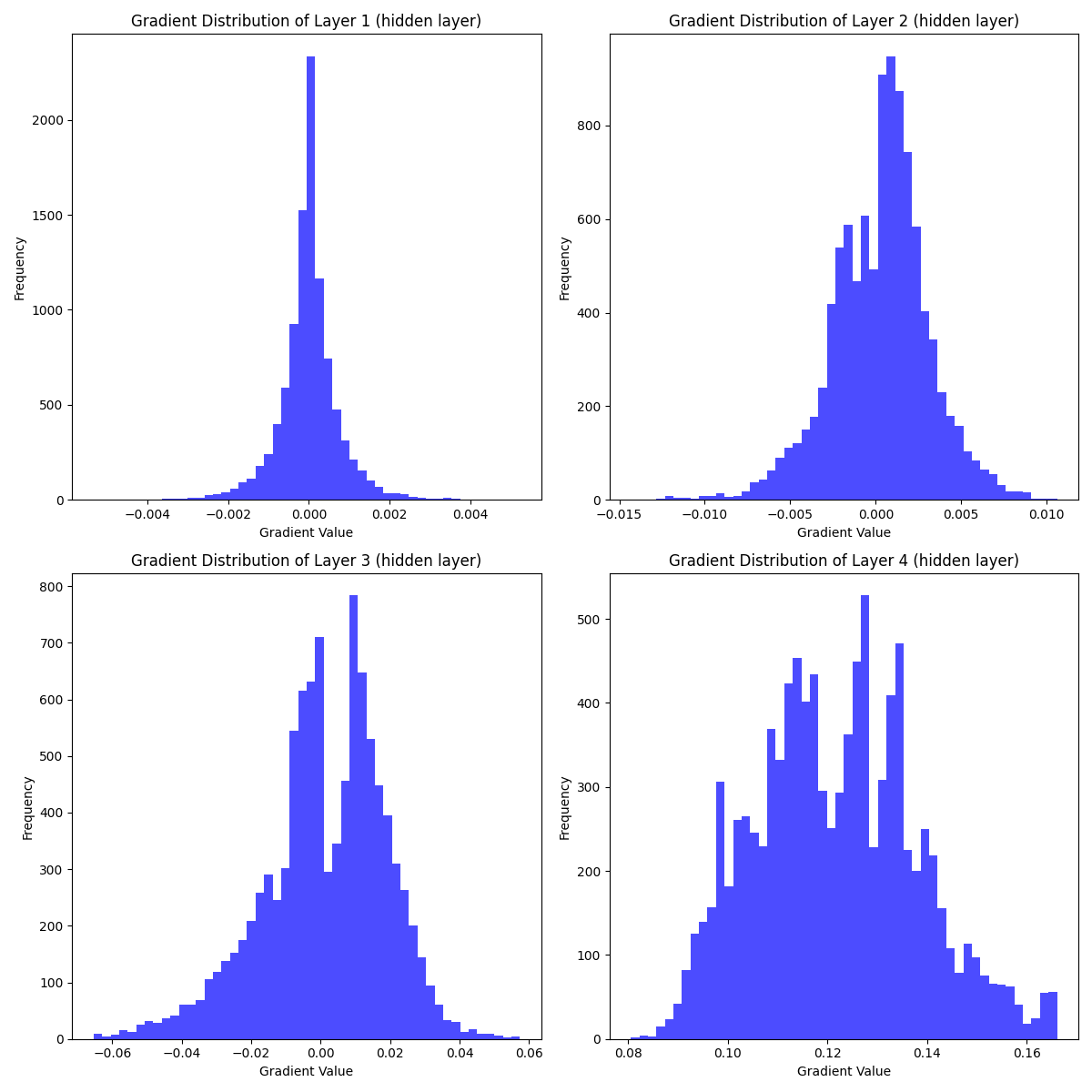
그리고 이제 망했다. 원래라면 layer1은 그렇다 치더라도 layer2, 3, 4는 모두 양수가 나왔어야되는데 그냥 zero-centered 되어버렸다. 왜 그런걸까.

생각해보니 역전파에 필요한 local gradient 중 구하지 않은 친구가 있었다. sigmoid 함수의 출력값이 다음 layer의 입력값이 되는 노드가 존재한다. 따라서 $g(x) =\sum_i w_ix_i +b$ 를 $x$에 대해서도 미분해야한다.

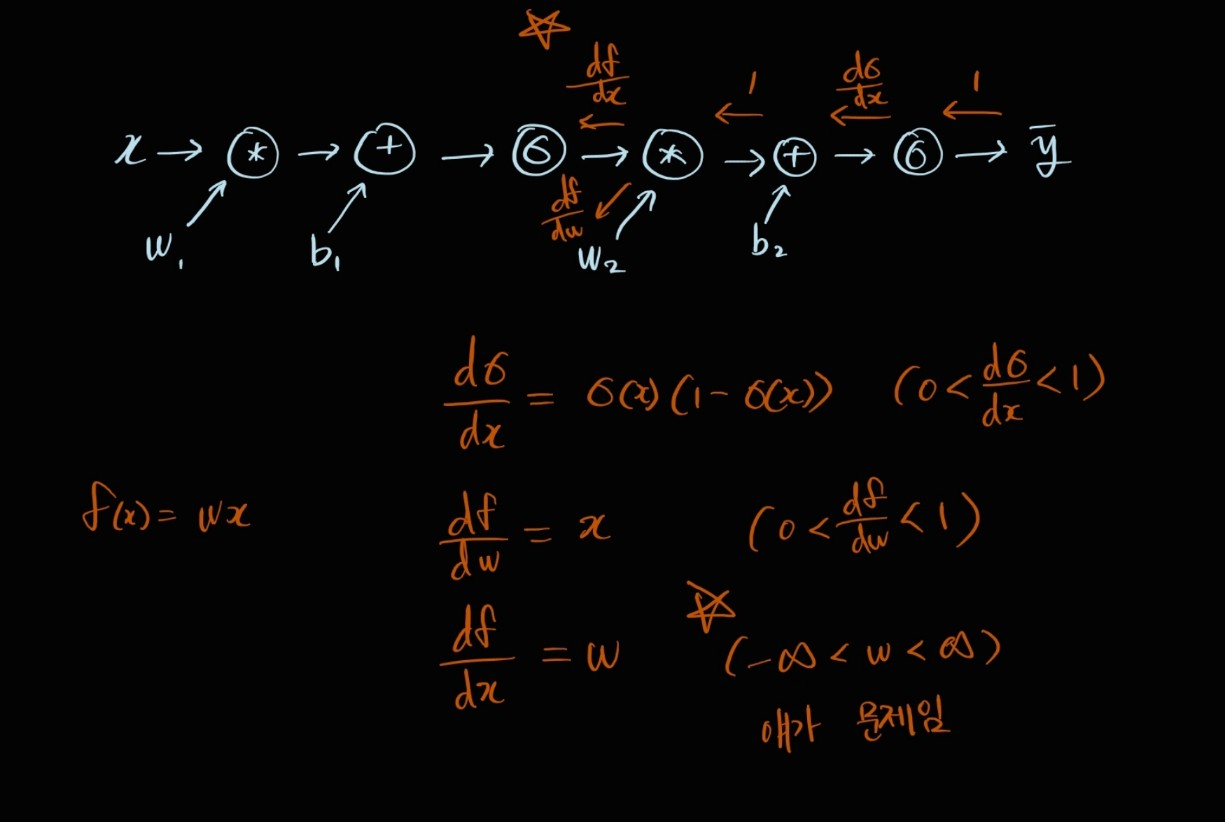
결국 첫번째 레이어의 가중치는 모두 양수가 되는 것이 맞지만, 그 이후로는 $w$가 local gradient에 들어가면서 부호가 바뀐다. 이런식으로 생각하면 딱히 학습에 지장이 없지 않을까 싶은데, 마지막 레이어는 결국 앞서 얘기했던 대로 모든 가중치가 동일한 방향으로 업데이트 될 수 밖에 없다.

sigmoid를 사용할 경우, 마지막 레이어의 가중치는 모두 같은 방향으로 업데이트 된다.

v3.0

zero-centered activation function 인 Tanh 을 사용해서 비교해보자

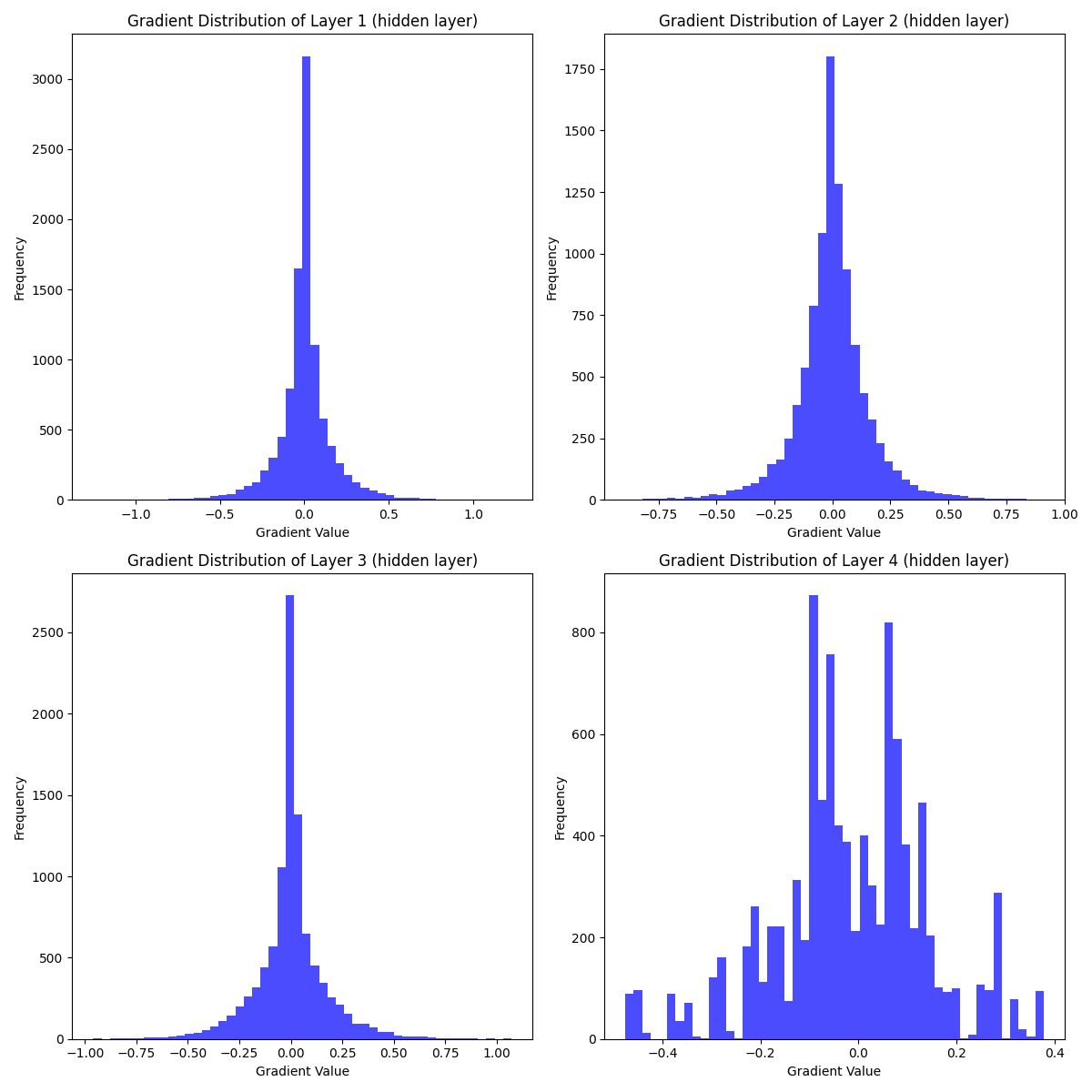
마지막 레이어에서도 gradients가 양수, 음수 상관없이 분배되어 있는 것을 확인할 수 있다. 그런데 아직 gradient-vanishing problem은 남아있어 보인다.

결론

1. Sigmoid 함수를 사용할 경우 마지막 레이어의 gradient 부호가 통일된다.
2. 마지막 출력값에만 Sigmoid를 사용하는 것은 학습에 전혀 지장이 없다.
3. Tanh 함수를 사용하면 zero-centered problem을 해결할 수 있다.

뭐 너무 당연한 결론이 나온 것 같은데 아무튼 그렇다. 1번에서 마지막 레이어의 gradient만 통일 되니까 사실상 학습에 크리티컬한 문제는 없는거 아닌가 싶긴 한데, zero-centered한 함수에 비하면 확실히 비효율적이다. 계층 사이 출력값이 편향되지 않도록 batch-normalization도 하는데, 레이어 출력값이 0과 1 사이로 한정되면 학습이 비효율적으로 진행될 수밖에 없다.

코드

import torch
import torch.nn as nn
from torch.autograd import Variable
import matplotlib.pyplot as plt


# 신경망 클래스 정의
class LayerSigmoidNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(LayerSigmoidNN, self).__init__()
        # 첫 번째 레이어: 입력 크기에서 은닉 레이어 크기로의 선형 변환
        self.layers = []
        self.layers.append(nn.Linear(input_size, hidden_size))
        self.layers.append(nn.Linear(hidden_size, hidden_size))
        self.layers.append(nn.Linear(hidden_size, hidden_size))
        self.layers.append(nn.Linear(hidden_size, output_size))

        # 시그모이드 활성화 함수
        self.sigmoid = nn.Tanh()

        self.layer_gradients = None
        self.sigmoid.register_forward_hook(self.get_intermediate_outputs)
        self.register_full_backward_hook(self.get_intermediate_gradients)

    def forward(self, x):
        # 순방향 전파를 정의합니다.

        out = None
        for i, layer in enumerate(self.layers):
            if i == 0:
                out = layer(x)
            else:
                out = layer(out)
            out = self.sigmoid(out)

        return out

    def get_intermediate_outputs(self, layer, inputs, outputs):
        print(outputs)

    # store gradient to member variable
    def get_intermediate_gradients(self, model, inputs, outputs):
        # 중간 레이어의 gradient 값을 추출
        print("[+] storing gradient value")
        print(len(outputs))
        self.layer_gradients = [layer.weight.grad for layer in self.layers]


# 입력, 은닉 레이어 크기 및 출력 크기 정의
input_size = 100
hidden_size = 100
output_size = 100

# 신경망 인스턴스 생성
model = LayerSigmoidNN(input_size, hidden_size, output_size)

# 모델 구조 확인
print("=" * 20)
print("[i] Model Structure")
print(model)
print("=" * 20)

# 모델의 입력 데이터 생성
input_data = Variable(torch.randn(1, input_size), requires_grad=True)

# 모델의 순방향 전파
output = model(input_data)

# 손실 함수 및 역전파 (예시에서는 필요 없음)
loss = torch.sum(output)
# target = torch.tensor(100.)
# loss = torch.nn.functional.mse_loss(torch.sum(output), target)
loss.backward()

# print(model.layers[0].weight.detach().numpy())

# 중간 레이어의 gradient 값을 시각화 (히스토그램)
print("[i] shape of gradient : ")


# show by matplotlib histogram
plt.figure(figsize=(12, 12))

# add each layer's gradient to figure
for idx, layer_gradient in enumerate(model.layer_gradients):
    print("\tlayer{} : {}".format(idx+1, layer_gradient.shape))

    gradient_value = layer_gradient.detach().numpy()

    plt.subplot(2, 2, idx + 1)

    plt.hist(gradient_value.flatten(), bins=50, color='blue', alpha=0.7)
    plt.title("Gradient Distribution of Layer {} (hidden layer)".format(idx+1))
    plt.xlabel("Gradient Value")
    plt.ylabel("Frequency")

# show
plt.tight_layout()
plt.show()