트리의 기본 개념
트리(Tree)란, 배열, 링크드리스트, 스택, 큐와 같이 일직선 개념의 자료구조가 아니라 부모-자식 개념을 가지는 자료구조이다.
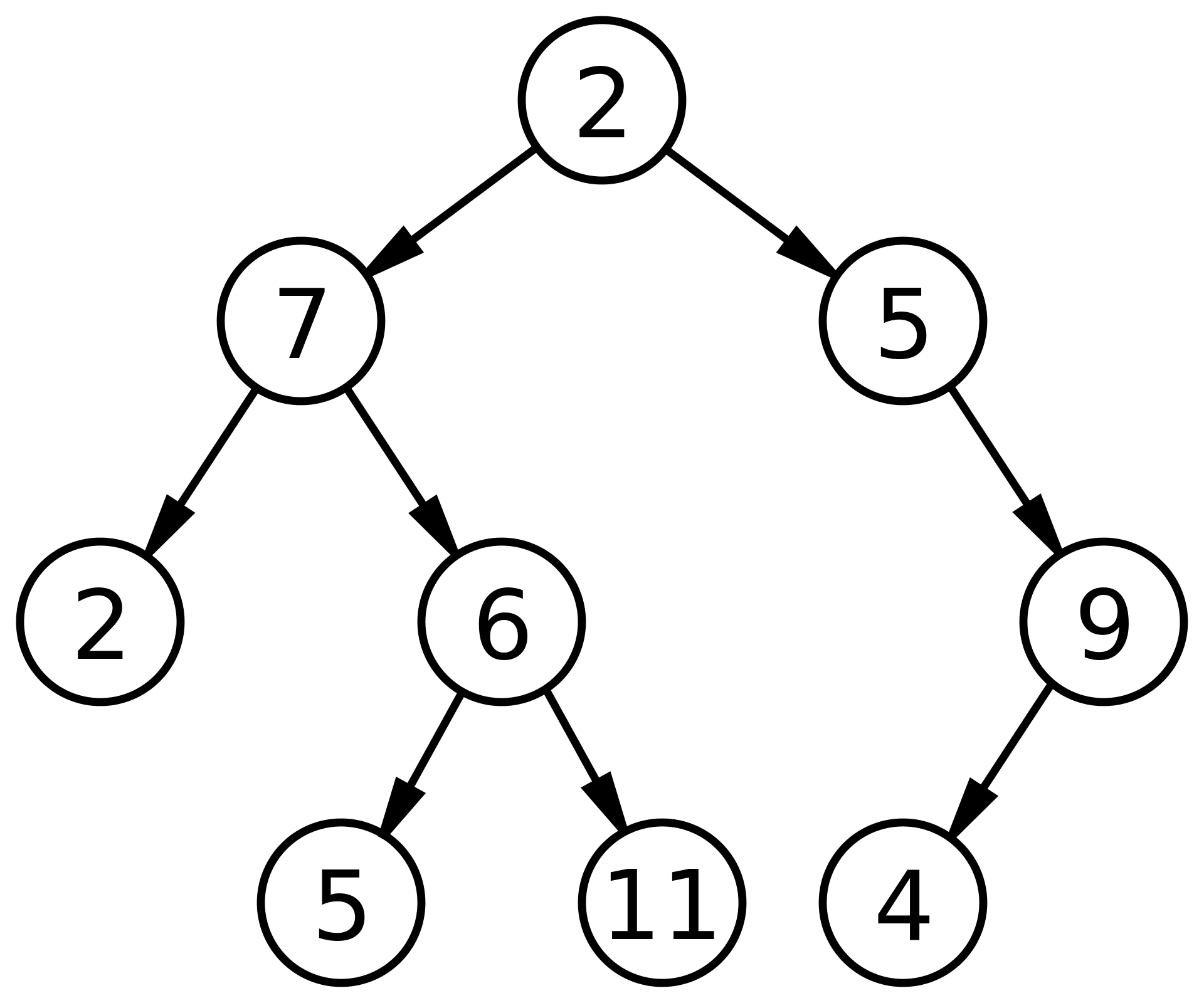
(출처 : 위키피디아)
트리는 위 그림처럼 표현이 되는 자료구조인데, 여기서 원으로 표시되는 2, 7, 5 등을 노드라고 하고 2는 7과 5의 부모(Parent), 7과 5는 2의 자식(Child)이다.
트리는 그래프의 일종이며, 두 개 이상의 노드가 하나의 노드를 가리킬 수 없다.
즉, 7과 6이 동시에 2를 가리킬 수 없다.
또한, 그렇기에 사이클이 생길 수 없다.
트리에서 최상위 즉, 맨 위에 있는 노드를 루트 노드(root node)라고 하며, 그림에서는 2가 루트 노드가 된다.
루트 노드는 당연히 최상위에 위치하기 때문에 부모를 가지지 않는다.
또한, 트리에서는 더 이상 자식이 없는 노드를 잎 노드(leaf node)라고 표현하고 그 반대로 자식을 하나 이상 가지는 노드를 내부 노드(internal node)라고 한다.
위 그림에서는 2, 5, 11, 4 노드가 leaf node이며, 그 나머지 노드가 internal node가 된다.
트리의 종류 - 이진 트리
이진 트리(binary tree)
이진 트리는 자식을 최대 2개까지만 가질 수 있는 트리이다.
이진 탐색 트리(binary search tree)

(출처 : 위키피디아)
이진 탐색 트리는 기본적인 특징은 이진 트리와 같지만 하나 다른 점은 자기 왼쪽에는 자신보다 값이 작은 노드가, 오른쪽에는 자신보다 값이 큰 노드가 와야한다는 것이다.
그래서 그림상 보면 루트 노드인 노드 8 왼쪽에는 8보다 작은 3, 1, 6, 4, 7이 있고 오른쪽에는 8보다 큰 10, 14, 13이 있다.
이 조건은 꼭 직속 부모-자식 관계에만 영향을 미치는 것이 아니다.
4를 기준으로 생각해보면, 3도 결국엔 자기보다 왼쪽에 있는 노드이므로 자신보다 작아야 하고, 1도 자기보다 왼쪽에 있는 노드이므로 당연히 4보다 작다.
반면, 13은 자기보다 오른쪽에 있으므로 당연히 크다.
이렇게 특정 노드를 기준으로 왼쪽에는 보다 작은 값이, 오른쪽에는 보다 큰 값을 가진 노드가 위치한 트리를 이진 탐색 트리라고 한다.
완전 이진 트리(complete binary tree)
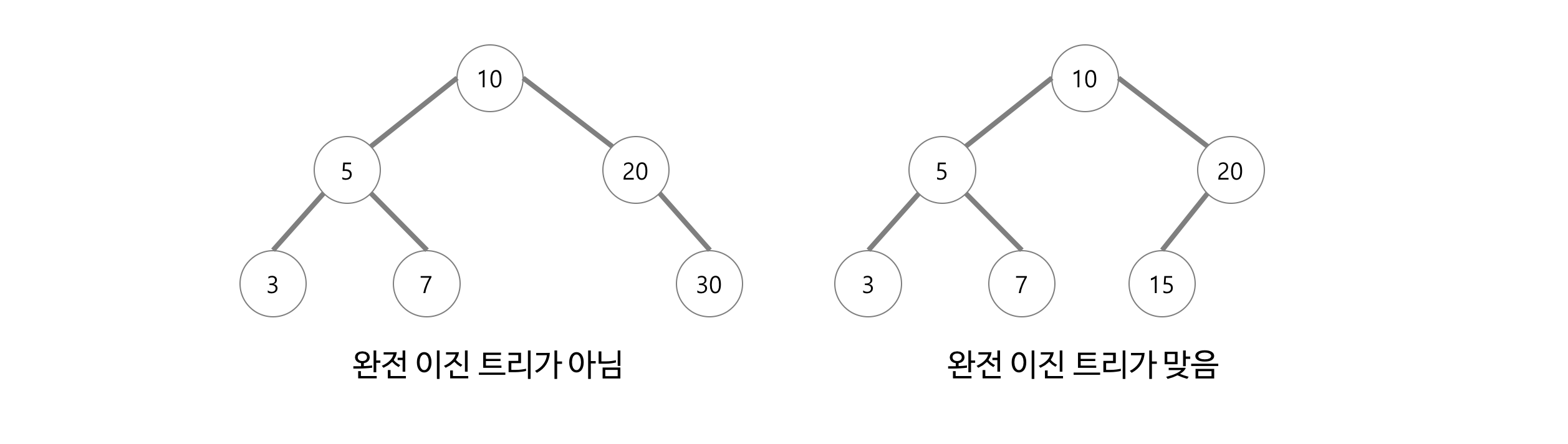
(출처 : gwlwjd9405.github.io)
완전 이진 트리는 이진 트리의 조건을 만족하면서 아래 조건을 만족해야 한다.
1. 마지막 레벨(위 그림에서는 레벨 3)을 제외한 나머지 레벨에서는 노드들이 꽉 차있어야 한다.
2. 마지막 레벨은 왼쪽부터 노드가 채워져 있어야 한다.
위 그림 왼쪽 트리가 완전 이진 트리가 되지 못하는 이유는 마지막 레벨에서 왼쪽부터 노드를 채우지 않았기 때문이다.(20의 자식인 30이 왼쪽이 아닌 오른쪽에 있다.)
full binary tree
full binary tree는 이진 트리의 조건을 만족하면서 아래 조건을 만족해야 한다.
1. 루트 노드를 제외한 모든 노드들은 2개의 자식 노드를 가지거나 자식 노드가 하나도 없어야 한다.
따라서, 위 완전 이진 트리 그림에서 노드 15가 없어진다면 full binary tree입니다.
perfect binary tree

(출처 : geeksforgeeks.org)
perfect binary tree가 되기 위한 조건은 이진 트리 조건을 만족하면서 아래 조건을 만족해야 한다.
1. 마지막 레벨에 있는 노드를 제외한 모든 나머지 노드들이 2개의 자식 노드를 가져야 한다.
