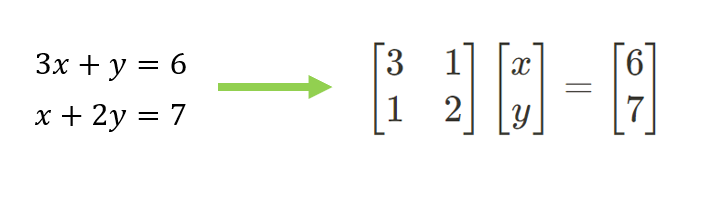[선형대수학] 행렬(1) - 행렬의 정의 및 기본연산

김기정·2024년 4월 23일
matrix선형대수학행렬
0

선형대수학

목록 보기
2/6

이번 포스팅에서는 행렬을 주제로 다뤄보겠습니다.

위키백과에 따르면 수학에서의 행렬은 다항식을 직사각형의 모양으로 배열한 것입니다. x, y의 변수를 가진 다항식에 대해 살펴보겠습니다.

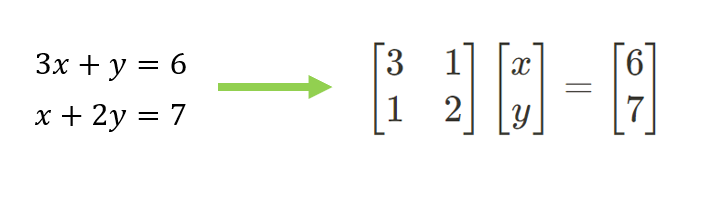
위 다항식의 값을 행렬의 연산을 이용해 해결하면 다음과 같습니다.

sol>

[3112][xy]=[67]⇒[6212][xy]=[127]⇒[5012][xy]=[57]⇒x=1 & y=3\begin{matrix} \begin{bmatrix} 3&1 \\ 1&2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 6 \\ 7 \end{bmatrix} &\Rightarrow& \begin{bmatrix} 6&2 \\ 1&2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 12 \\ 7 \end{bmatrix} \\ \\ &\Rightarrow& \begin{bmatrix} 5&0 \\ 1&2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 5 \\ 7 \end{bmatrix} \\ \\ &\Rightarrow& x=1\ \& \ y=3 \end{matrix}

행렬은 이처럼 다항식을 표현하고 해를 구하는 목적 그리고 수들을 표현하기 위한 목적으로 사용되고 있습니다. 이 행렬에 대해 정의부터 차근차근 알아보겠습니다.

Def> matrix

위키백과의 정의는 위와 같습니다. 즉, 사각형에 숫자들을 담고 있는데 그 숫자(= aija_{ij})들이 순서가 있는 숫자들의 배열(Array)이라 할 수 있을 것 같습니다. ii가 행(row)을 의미하고 jj는 열(column)을 의미합니다.

그리고 aija_{ij}가 실수 영역인지 복소수 영역인지에 따라 실수 행렬, 복소수 행렬이라 합니다. 이번 포스팅에서는 실수 행렬(real matrix)만 다루겠습니다.

Notation

행렬은 기본적으로 "[]" 혹은 "()"를 통해 묶어서 표현합니다. 다음은 m×nm \times n 행렬의 표현방법입니다.

A=[a11a12a13⋯a1na21a22a23⋯a2na31a32a33⋯a3n⋮⋮⋮⋱⋮am1am2am3⋯amn]=(a11a12a13⋯a1na21a22a23⋯a2na31a32a33⋯a3n⋮⋮⋮⋱⋮am1am2am3⋯amn)A = \begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn} \\ \end{bmatrix} = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn} \\ \end{pmatrix} \\

행렬의 기본연산에 들어가기 앞서 Numpy 모듈을 소개하려 합니다. Numpy는 Python언어의 matrix연산을 수행할 수 있는 모듈이고 이번 포스팅에서도 사용하려 합니다.

기본 연산

행렬의 연산인 ++(Addition), ⋅\cdot(Scalar multiplication), −-(Subtraction), TT(Transposition)에 대해 알아보겠습니다.

Addition

For m×nm \times n matrix AA and BB,

A+B=[a11+b11a12+b12a13+b13⋯a1n+b1na21+b21a22+b22a23+b23⋯a2n+b2na31+b31a32+b32a33+b33⋯a3n+b3n⋮⋮⋮⋱⋮am1+bm1am2+bm2am3+bm3⋯amn+bmn]A + B = \begin{bmatrix} a_{11}+b_{11} & a_{12}+b_{12} & a_{13}+b_{13} & \cdots & a_{1n}+b_{1n} \\ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} & \cdots & a_{2n}+b_{2n} \\ a_{31}+b_{31} & a_{32}+b_{32} & a_{33}+b_{33} & \cdots & a_{3n}+b_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2} & a_{m3}+b_{m3} & \cdots & a_{mn}+b_{mn} \\ \end{bmatrix}

example : 2×32 \times 3 matrix AA and BB

A=[131100],B=[005750]A = \begin{bmatrix} 1 & 3 & 1 \\ 1 & 0 & 0 \end{bmatrix}, \quad B = \begin{bmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \end{bmatrix} \\

sol>

A+B=[1+03+01+51+70+50+0]=[136850]\\ A + B = \begin{bmatrix} 1+0 & 3+0 & 1+5 \\ 1+7 & 0+5 & 0+0 \end{bmatrix} = \begin{bmatrix} 1 & 3 & 6 \\ 8 & 5 & 0 \end{bmatrix}

python code

import numpy as np

A = np.array([[1,3,1],
              [1,0,0]])
B = np.array([[0,0,5],
              [7,5,0]])

print(f"A\n{A}")

print(f"B\n{B}")

print(f"A + B \n{A + B}")

result

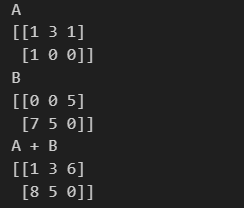
Scalar multiplication

For c∈Rc \in \R and n×mn \times m matrix A,

c⋅A=[c⋅a11c⋅a12c⋅a13⋯c⋅a1nc⋅a21c⋅a22c⋅a23⋯c⋅a2nc⋅a31c⋅a32c⋅a33⋯c⋅a3n⋮⋮⋮⋱⋮c⋅am1c⋅am2c⋅am3⋯c⋅amn]c \cdot A = \begin{bmatrix} c\cdot a_{11} & c\cdot a_{12} & c\cdot a_{13} & \cdots & c\cdot a_{1n} \\ c\cdot a_{21} & c\cdot a_{22} & c\cdot a_{23} & \cdots & c\cdot a_{2n} \\ c\cdot a_{31} & c\cdot a_{32} & c\cdot a_{33} & \cdots & c\cdot a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ c\cdot a_{m1} & c\cdot a_{m2} & c\cdot a_{m3} & \cdots & c\cdot a_{mn} \\ \end{bmatrix}

example : 2×32 \times 3 matrix AA and c∈Rc \in \R

c=2andA=[18−34−25]c=2 \quad \text{and} \quad A = \begin{bmatrix} 1 & 8 & -3 \\ 4 & -2 & 5 \end{bmatrix}

sol>

c⋅A=[2⋅12⋅82⋅(−3)2⋅42⋅(−2)2⋅5]=[216−68−410]c \cdot A = \begin{bmatrix} 2\cdot 1 & 2\cdot 8 & 2\cdot (-3) \\ 2\cdot 4 & 2\cdot (-2) & 2\cdot 5 \end{bmatrix} = \begin{bmatrix} 2 & 16 & -6 \\ 8 & -4 & 10 \end{bmatrix}

python code

import numpy as np

A = np.array([[1,8,-3],
              [4,-2,5]])
c = 2

print(f"A\n{A}")
print(f"c = {c}")

print(f"cA \n{c * A}")

result

Subtraction

For m×nm \times n matrix AA and BB,

A−B=A+(−1)⋅BA - B = A + (-1)\cdot B

example : 2×32 \times 3 matrix AA and BB

A=[123654],B=[18−34−25]A = \begin{bmatrix} 1 & 2 & 3 \\ 6 & 5 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 1 & 8 & -3 \\ 4 & -2 & 5 \end{bmatrix}

sol>

A−B=A+(−1)⋅B=[123654]+(−1)⋅[18−34−25]=[123654]+[−1−83−42−5]=[0−6627−1]\begin{matrix} A - B &=& A + (-1)\cdot B \\ \\ &=& \begin{bmatrix} 1 & 2 & 3 \\ 6 & 5 & 4 \end{bmatrix} +(-1) \cdot \begin{bmatrix} 1 & 8 & -3 \\ 4 & -2 & 5 \end{bmatrix} \\ \\ &=& \begin{bmatrix} 1 & 2 & 3 \\ 6 & 5 & 4 \end{bmatrix} + \begin{bmatrix} -1 & -8 & 3 \\ -4 & 2 & -5 \end{bmatrix} \\ \\ &=& \begin{bmatrix} 0 & -6 & 6 \\ 2 & 7 & -1 \end{bmatrix} \end{matrix}

python code

import numpy as np

A = np.array([[1,2,3],
              [6,5,4]])

B = np.array([[1,8,-3],
              [4,-2,5]])
c = -1

print(f"A\n{A}\n")

print(f"B\n{B}\n")

print(f"c = {c}\n")

print(f"A - B\n{A - B}\n")

print(f"A + (-1) * B \n{A + (-1) * B}\n")

result

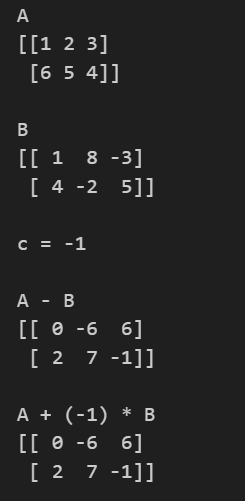
Transposition

For m×nm \times n matrix AA,

AT=[a11a21a31⋯am1a12a22a32⋯am2a13a23a33⋯am3⋮⋮⋮⋱⋮a1na2na3n⋯amn]:n×m   matrixA^T = \begin{bmatrix} a_{11} & a_{21} & a_{31} & \cdots & a_{m1} \\ a_{12} & a_{22} & a_{32} & \cdots & a_{m2} \\ a_{13} & a_{23} & a_{33} & \cdots & a_{m3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & a_{3n} & \cdots & a_{mn} \\ \end{bmatrix} : n \times m\ \ \ \text{matrix}

example : 2×32 \times 3 matrix AA

A=[123654]⇒AT=[162534]A = \begin{bmatrix} 1 & 2 & 3 \\ 6 & 5 & 4 \end{bmatrix} \Rightarrow A^T = \begin{bmatrix} 1 & 6 \\ 2 & 5 \\ 3 & 4 \end{bmatrix}

python code

import numpy as np

A = np.array([[1,2,3],
              [6,5,4]])


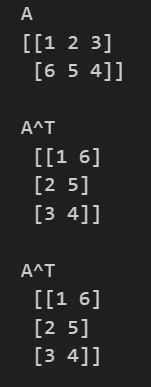
print(f"A\n{A}\n")

print(f"A^T \n {A.T}\n")

print(f"A^T \n {A.transpose()}")

result

이렇게 기본 연산 과정에 대해 다뤄 보았습니다. 포스팅이 길어지는 만큼 행렬 곱셈, 선형 변환, 행렬의 노름, 행렬의 종류, 행렬식에 대해서는 다음 포스팅에 작성하겠습니다.

읽어주셔서 감사합니다. 오탈자 혹은 잘못된 내용이 있을 경우에 댓글 주시면 감사하겠습니다.

Reference

profile
김기정
끊임 없이 도전하는 개발자입니다.
이전 포스트

[선형대수학] 벡터와 노름

다음 포스트

[선형대수학] 행렬(2) - Product 및 선형변환

0개의 댓글