지난 포스팅 행렬(1) - 행렬의 정의 및 기본연산에 이어서 행렬의 곱셈(matrix multiplication), 선형변환(Linear Transformation)에 대해 알아보겠습니다.
matrix multiplication
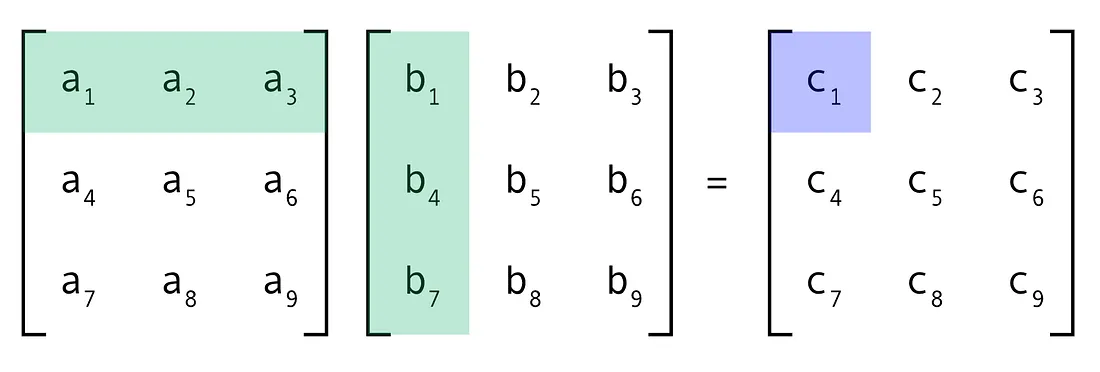
행렬의 곱셈 즉 행렬의 내적을 계산할 때는 위와 같이 "ㄱ"모양으로 진행하면 됩니다. 수식으로 설명하면 다음과 같습니다.
For m×n matrix A and n×p matrix B,
A=⎣⎢⎢⎢⎢⎢⎢⎡a11a21a31⋮am1a12a22a32⋮am2a13a23a33⋮am3⋯⋯⋯⋱⋯a1na2na3n⋮amn⎦⎥⎥⎥⎥⎥⎥⎤&B=⎣⎢⎢⎢⎢⎢⎢⎡b11b21b31⋮bn1b12b22b32⋮bn2b13b23b33⋮bn3⋯⋯⋯⋱⋯b1pb2pb3p⋮bnp⎦⎥⎥⎥⎥⎥⎥⎤
위와 같이 행렬 A, B가 정의되어 있습니다. 그럼 C=A⋅B는 다음과 같이 m×p인 행렬이 됩니다.
C=⎣⎢⎢⎢⎢⎢⎢⎡c11c21c31⋮cm1c12c22c32⋮cm2c13c23c33⋮cm3⋯⋯⋯⋱⋯c1pc2pc3p⋮cmp⎦⎥⎥⎥⎥⎥⎥⎤, cij==ai1b1j+ai2b2j+⋯+ainbnj<ai,bj>=∑k=1naikbkj
다시 말해 cij는 A의 i번째 row vector(=ai)와 B의 j번째 column vector(=bj)의 내적으로 구할 수 있습니다.
example
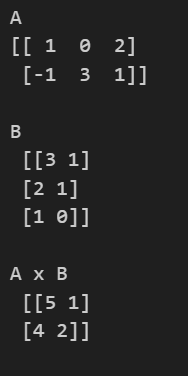
A=[1−10321],B=⎣⎢⎡321110⎦⎥⎤⇒A⋅B=?
sol>
A⋅B===[1−10321]⋅⎣⎢⎡321110⎦⎥⎤[1⋅3+0⋅2+2⋅1−1⋅3+3⋅2+1⋅11⋅1+0⋅1+2⋅0−1⋅1+3⋅1+1⋅0][5412]
import numpy as np
A = np.array([[1,0,2],
[-1,3,1]])
B = np.array([[3,1],
[2,1],
[1,0]])
print(f"A\n{A}\n")
print(f"B \n {B}\n")
print(f"A x B \n {np.dot(A,B)}")
result
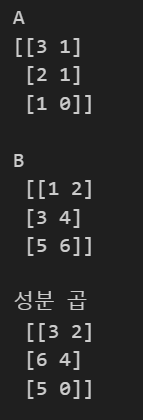
또한 numpy의 기능으로 행렬 각각의 성분 곱을 지원합니다. 이는 아래와 같습니다.
import numpy as np
A = np.array([[3,1],
[2,1],
[1,0]])
B = np.array([[1,2],
[3,4],
[5,6]])
print(f"A\n{A}\n")
print(f"B \n {B}\n")
print(f"성분 곱 \n {A * B}")
result
근데 만약 크기가 다른 행렬을 성분 곱을 취했을 때는 다음과 같은 Error가 발생합니다.

행렬과 벡터를 연산하는 데 있어서 size를 중요하게 고려해야합니다.
지금까지 행렬의 곱셈에 대해 설명하고 예제를 손으로 직접 구해도 보고 numpy를 이용해 구해봤습니다. 이제 부터는 행렬의 곱셈의 성질에 대해 알아보겠습니다.
Property1. Associativity
Let A be a m×n matrix & B be a n×p matrix & C be a p×q matrix.
we have that
A(BC)=(AB)C
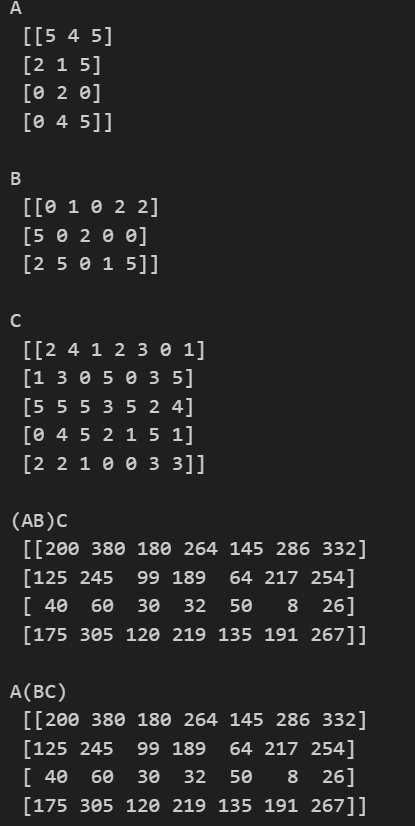
example> numpy를 이용해 무작위로 행렬을 만들고 값을 비교해보겠습니다.
Let A be a 4×3 matrix & B be a 3×5 matrix & C be a 5×7 matrix.
import numpy as np
A = np.random.randint(6, size=(4,3))
B = np.random.randint(6, size=(3,5))
C = np.random.randint(6, size=(5,7))
print(f"A \n {A}\n")
print(f"B \n {B}\n")
print(f"C \n {C}\n")
m1 = np.dot(np.dot(A,B),C)
m2 = np.dot(A, np.dot(B,C))
print(f"(AB)C \n {m1}\n")
print(f"A(BC) \n {m2}\n")
result>
Property 2. distributivity
Let A and B be m×n matrices & C be a n×p matrix.
we have that
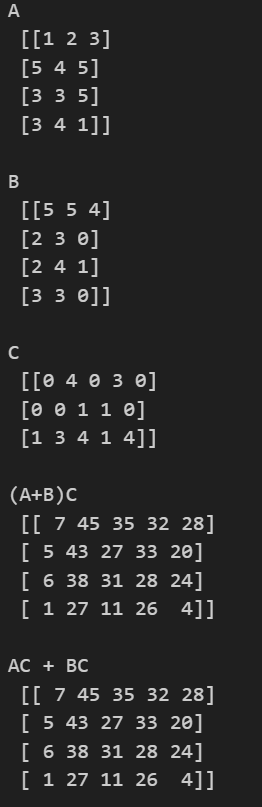
(A+B)C=AC+BC
example> numpy를 이용해 무작위로 행렬을 만들고 값을 비교해보겠습니다.
Let A and B be 4×3 matrices & C be a 3×5 matrix
import numpy as np
A = np.random.randint(6, size=(4,3))
B = np.random.randint(6, size=(4,3))
C = np.random.randint(6, size=(3,5))
print(f"A \n {A}\n")
print(f"B \n {B}\n")
print(f"C \n {C}\n")
r1 = np.dot((A + B),C)
r2 = np.dot(A,C) + np.dot(B,C)
print(f"(A+B)C \n {r1}\n")
print(f"AC + BC \n {r2}\n")
result>
당연하게도 다음도 성립합니다.
Let C be a m×n matrix & A and B be n×p matrices.
we have that
C(A+B)=CA+CB
그리고 matrix multiplication에서는 교환법칙(commutative)이 성립되지 않습니다.
commutative ? ⇒ 성립 x
당연하게 A가 a×b matrix이고 B가 b×c matrix 이면 애초에 행렬간의 곱셈을 취할 수 없습니다.
그리고 A,B가 n×n인 정방 행렬인 경우에 대해서 살펴보겠습니다.
Let AB=C and BA=C ′. and we have that
cij = ai1b1j+ai2b2j+⋯+ainbnj = k=1∑naikbkj,
cij ′ = bi1a1j+bi2a2j+⋯+binanj = k=1∑nbikakj
Socij=cij ′⇒C=C ′.
일반적으로 행렬의 곱셈에서 교환법칙은 성립하지 않습니다.
Row Operation(기본 행 연산)과 Linear equations(방정식)에 대해서는 다음에 다루도록 하겠습니다.
이제는 Linear Transformations(선형변환)에 대해 알아보겠습니다.
간단하게 선형 변환은 차원을 늘리거나 축소시키는 것을 의미합니다.
먼저 수학적으로 정의부터 살펴보겠습니다.
Let V,W be vector spaces over the same field F.
A function T:V→W is said to be a linear transformation if for any two vectors u,v∈V and any scalar k∈F the following two conditions ar satisfied:
- additivity : T(u+v)=T(u)+T(v)
- homogeneity : T(ku)=kT(u)
- T(ku+v)=kT(u)+T(v)
위키 백과를 통한 수학적 정의는 위와 같습니다. 예제를 들어 설명해보겠습니다.
example>
Let A be a m×n matrix
Au=v,with u∈Rn and v∈Rm,
즉 위에서는 n차원인 u 벡터가 m 차원인 v 벡터로 선형변환 된것입니다.
선형변환은 이후 차원 축소, 차원 확대, 고유값 고유벡터를 설명할 때 쓰이는 아주 중요한 개념 입니다.
추가적으로 더 궁금한 내용이나 포스팅에 오류가 있을 경우 댓글 부탁드립니다. 이번 포스팅은 여기서 마치겠습니다.
Reference






