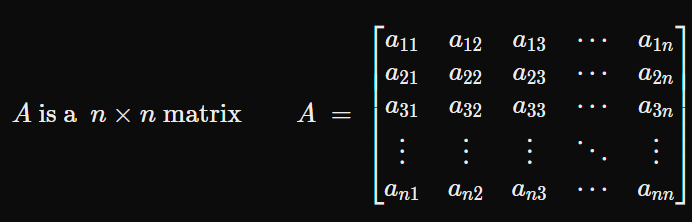[선형대수학] 행렬(3) - 정방행렬 및 행렬의 종류

김기정·2024년 5월 6일

Square matrix matrix 선형대수학 정방행렬 행렬

선형대수학

목록 보기

4/6

이번 포스팅은 정방행렬(Square matrix)에 대해 다뤄보겠습니다. 다시말해, 정방행렬이 무엇이고 정방행렬의 종류에 대한 내용을 알아보겠습니다.

정방행렬의 개념

먼저 정방행렬이란 행과 열의 크기가 같은 행렬을 말합니다. 즉, 다음과 같은 행렬입니다.

\begin{matrix} A \ \text{is a } \ n \times n \ \text{matrix} && A \ =\ \begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} \\ \end{bmatrix} \end{matrix}

이제는 정방행렬의 종류에 대해 살펴보겠습니다.

정방행렬의 종류

1. Diagonal matrix(대각행렬)

주 대각 성분을 제외한 모든 성분의 값이 0인 행렬을 말한다. 즉 $A$ 를 대각행렬이라 하면 다음과 같다.

A = \begin{bmatrix} a_{11} & 0 & 0 & \cdots & 0 \\ 0 & a_{22} & 0 & \cdots & 0 \\ 0 & 0 & a_{33} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{nn} \\ \end{bmatrix} ,\ \forall i, j \in \{1, \cdots, n\}, i \ne j \Rightarrow \ a_{ij} = 0

대각행렬의 표현방법(notation)은 다음과 같다.

\\ A = \begin{bmatrix} a_{1} & 0 & 0 & \cdots & 0 \\ 0 & a_{2} & 0 & \cdots & 0 \\ 0 & 0 & a_{3} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{n} \\ \end{bmatrix} = \text{diag}(a_1,\cdots,a_n)

2. Trianglar matrix(삼각행렬)

삼각행렬은 두 가지 종류가 있습니다. 대각선을 기준으로 나눌 수 있습니다.

upper triangular matrix(상삼각행렬)
주 대각 성분의 밑에 있는 성분들이 모두 0인 행렬이다.
$U = \begin{bmatrix} u_{11} & u_{12} & u_{13} & \cdots & u_{1n} \\ 0 & u_{22} & u_{23} & \cdots & u_{2n} \\ 0 & 0 & u_{33} & \cdots & u_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & u_{nn} \\ \end{bmatrix}, \begin{matrix} \forall i, j \in \{1,...,n\}, i> j \\ \qquad \Rightarrow u_{ij} = 0 \end{matrix}$
lower triagular matrix(하삼각행렬)
주 대각 성분의 위에 있는 성분들이 모두 0인 행렬이다.
$L = \begin{bmatrix} l_{11} & 0 & 0 & \cdots & 0 \\ l_{21} & l_{22} & 0 & \cdots & 0 \\ l_{31} & l_{32} & l_{33} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ l_{n1} & l_{n2} & l_{n3} & \cdots & l_{nn} \\ \end{bmatrix}, \begin{matrix} \forall i, j \in \{1,...,n\}, i< j \\ \qquad \Rightarrow l_{ij} = 0 \end{matrix}$

3. Identity matrix(항등행렬)

항등행렬은 대각행렬중에서 대각 성분의 모든 값이 1인 행렬을 의미한다.
즉 다음과 같은 행렬을 말합니다.

I_n \ =\ \text{diag}(1,\cdots,1) \ = \ \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ \end{bmatrix}_{n \times n}

그리고 이 항등행렬은 다음을 만족합니다.
Let $A$ be a $m \times n$ matrix.

I_m A = A = AI_n

다른 행렬과 행렬곱셈(matrix multiplication)을 취해도 자기 자신의 행렬이 나옵니다. 즉 행렬의 행렬곱셈 연산에서 항등원(identity element)가 되는 것입니다.

4. Inverse matrix(역행렬)

def> Invertible matrix(가역행렬)
Let $A, B$ be $n \times n$ matrices
$A$ is called "invertible matrix" if $\exist! \ B$ such that $AB = BA = I_n$

이때 $B$ 를 $A$ 에 대응하는 역행렬(inverse matrix, $A^{-1}$ )이라 한다.

example> $n \times n$ Matrix A is invertible?
Gaussian elimination 방법을 사용해 행렬 $A$ 의 역행렬을 구해보겠습니다.

$A = \begin{bmatrix} -1& 3/2 \\ 1&-1 \end{bmatrix}$

solution>
step 1 : Create the augmented matrix [ $A|I_2$ ]

A \ = \ \begin{bmatrix} -1& 3/2 \\ 1&-1 \end{bmatrix} \quad \Rightarrow \quad \left[ \begin{array}{cc|cc} -1 & {3 \over 2} & 1 & 0 \\ 1 & -1 & 0 & 1 \\ \end{array} \right]

step 2 : Elementary row operation : $R_1 + R_2 \rightarrow R_2$

\left[ \begin{array}{cc|cc} -1 & {3 \over 2} & 1 & 0 \\ 1 & -1 & 0 & 1 \\ \end{array} \right] \quad \Rightarrow \quad \left[ \begin{array}{cc|cc} -1 & {3 \over 2} & 1 & 0 \\ 0 & {1 \over 2} & 1 & 1 \\ \end{array} \right]

step 3 : Elementary row operation : $R_1 - 3R_2 \rightarrow R_1$

\left[ \begin{array}{cc|cc} -1 & {3 \over 2} & 1 & 0 \\ 0 & {1 \over 2} & 1 & 1 \\ \end{array} \right] \quad \Rightarrow \quad \left[ \begin{array}{cc|cc} -1 & 0 & -2 & -3 \\ 0 & {1 \over 2} & 1 & 1 \\ \end{array} \right]

step 4 : Elementary row operation : $-R_1\rightarrow R_1 \ \& \ 2R_2\rightarrow R_2$

\left[ \begin{array}{cc|cc} -1 & 0 & -2 & -3 \\ 0 & {1 \over 2} & 1 & 1 \\ \end{array} \right] \quad \Rightarrow \quad \left[ \begin{array}{cc|cc} 1 & 0 & 2 & 3 \\ 0 & 1 & 2 & 2 \\ \end{array} \right]

So we have that $A^{-1} = \begin{bmatrix} 2 & 3 \\ 2 & 2 \end{bmatrix}$

$A = \begin{bmatrix} 2&4 \\ 1&2 \end{bmatrix}$

위의 예제는 불가능 합니다. 왜냐하면 기본행 연산을 통해 항등행렬로 만들 수 없기 때문입니다. 역행렬에 대한 것은 다음 포스팅에서 더 자세하게 다루도록하겠습니다.

5. Symmetric matrix(대각행렬)

대각행렬은 정방행렬의 $A$ 의 전치행렬 $A^T$ 과 $A$ 가 같은 행렬을 말합니다.

Def> Symmetric matrix
The square matrix A that is equal to its transpose. ( $i.e. \ A = A^T$ )

Example> $A$ is a $3 \times 3$ matrix.

A = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{bmatrix} \quad \rightarrow \quad A = A^T

또한 $-A = A^T$ 인 경우 $A$ 를 skew-symmetric matrix라 합니다.

6. Definite matrix(정방향행렬)

정방향행렬은 행렬의 부호를 나타냅니다. 즉 벡터를 선형변환을 했을 때 선형변환된 벡터와 자기자신의 벡터와의 내적의 값의 부호로 결정됩니다.

Let $A$ be a $n \times n$ symmetric matrix.

$\forall v \in \R^n \backslash \{\vec0\}$ , (either semi positive and semi negative : $\forall v \in \R^n$ )

Q(v)\quad = \quad v^TAv \quad = \quad <v,Av>

positive definite matrix : $Q(v) > 0, \forall v \in \R^n \backslash \{\vec0\}$
semi positive definite matrix : $Q(v) \ge 0, \forall v \in \R^n$
negative definite matrix : $Q(v) < 0, \forall v \in \R^n \backslash \{\vec0\}$
semi negative definite matrix : $Q(v) \le 0, \forall v \in \R^n$

모든 대각 행렬이 위 4가지로 분류되진 않습니다. 0인 경우 0보다 작은 경우 0보다 큰 경우 다 존재할 수도 있습니다. 이 경우 행렬 $A$ 를 indefinite matrxi라 합니다.

example> numpy를 이용해 무작위 벡터의 $Q(v)$ 확인

import numpy as np

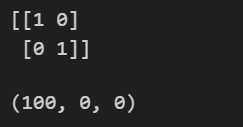
A = np.array([[1,0],[0,1]])

T = 100

p, n, e = 0, 0, 0

print(A)

for _ in range(T):
    v = np.random.randn(2)
   	while not np.linalg.norm(v,1):
        v = np.random.randn(2)
    inner = np.dot(v,np.dot(A, v))
    if inner > 0:
        p += 1
    elif inner < 0:
        n += 1
    else:
        e += 1
        
p, n, e