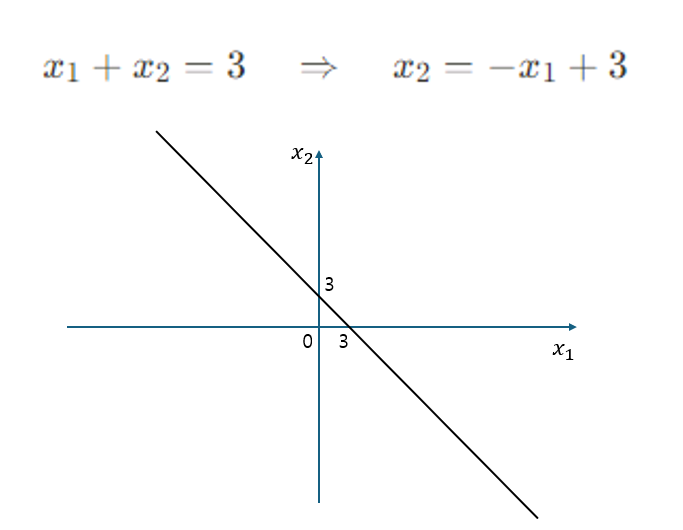이번 포스팅에서는 기본행 연산에 대해 알아보겠습니다.
행렬은 처음 행렬(1) 을 살펴보면 다항
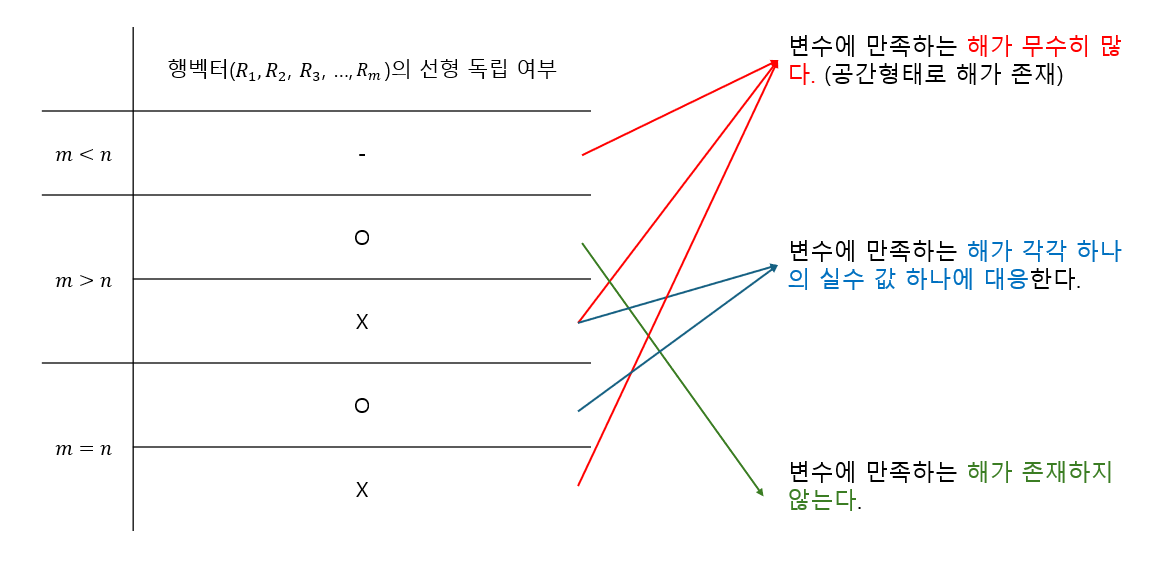
연립방정식의 해의 존재 여부
다항식이 다음과 같이 존재한다고 했을 때 식의 개수는 m m m n n n
{ a 11 x 1 + a 12 x 2 + a 13 x 3 + ⋯ + a 1 n x n = y 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + ⋯ + a 2 n x n = y 2 a 31 x 1 + a 32 x 2 + a 33 x 3 + ⋯ + a 3 n x n = y 3 ⋮ a m 1 x 1 + a m 2 x 2 + a m 3 x 3 + ⋯ + a m n x n = y m \begin{cases} a_{11}x_1 + a_{12}x_2 + a_{13}x_3 + \cdots + a_{1n}x_n &=&y_1 \\ a_{21}x_1 + a_{22}x_2 + a_{23}x_3 + \cdots + a_{2n}x_n &=&y_2 \\ a_{31}x_1 + a_{32}x_2 + a_{33}x_3 + \cdots + a_{3n}x_n &=&y_3 \\ \qquad \qquad \qquad \qquad \vdots \\ a_{m1}x_1 + a_{m2}x_2 + a_{m3}x_3 + \cdots + a_{mn}x_n &=&y_m \end{cases} ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ a 1 1 x 1 + a 1 2 x 2 + a 1 3 x 3 + ⋯ + a 1 n x n a 2 1 x 1 + a 2 2 x 2 + a 2 3 x 3 + ⋯ + a 2 n x n a 3 1 x 1 + a 3 2 x 2 + a 3 3 x 3 + ⋯ + a 3 n x n ⋮ a m 1 x 1 + a m 2 x 2 + a m 3 x 3 + ⋯ + a m n x n = = = = y 1 y 2 y 3 y m 그럼 우리는 3가지 경우를 찾을 수 있습니다. 변수의 개수가 식의 개수보다 많을 때(n > m n > m n > m n < m n < m n < m n = m n = m n = m
1. n > m n > m n > m :
예를 들어 다음과 같이 m = 1이고 n = 2인 경우를 살펴보겠습니다.
x 1 + x 2 = 3 x_1 + x_2 = 3 x 1 + x 2 = 3 이때 x 1 , x 2 x_1, x_2 x 1 , x 2
이 경우에는 변수 값이 무수히 많이 존재하게 됩니다.
2. n < m n < m n < m :
case 1> 존재하는 경우
{ x 1 + x 2 = 2 ⋯ ( R 1 ) x 1 + 3 x 2 = 4 ⋯ ( R 2 ) − x 1 + x 2 = 0 ⋯ ( R 3 ) ⇒ { x 1 + x 2 = 2 − x 1 + x 2 = 0 − x 1 + x 2 = 0 ( R 2 − 2 R 1 → R 2 ) ⇒ { x 1 + x 2 = 2 − x 1 + x 2 = 0 0 ⋅ x 1 + 0 ⋅ x 2 = 0 ( R 3 − R 2 → R 3 ) \begin{matrix} \begin{cases} x_1 + x_2 &=& 2 \ \cdots\ (R_1) \\ x_1 + 3x_2 &=& 4 \ \cdots\ (R_2) \\ -x_1 + x_2 &=& 0 \ \cdots\ (R_3) \end{cases} & \Rightarrow & \begin{cases} x_1 + x_2 &=& 2 \\ -x_1 + x_2 &=& 0 \\ -x_1 + x_2 &=& 0 \end{cases} \quad (R_2-2R_1 \rightarrow R_2) \\ \\ & \Rightarrow & \begin{cases} x_1 + x_2 &=& 2 \\ -x_1 + x_2 &=& 0 \\ 0\cdot x_1 +0\cdot x_2 &=& 0 \end{cases} \quad (R_3-R_2 \rightarrow R_3) \end{matrix} ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 1 + x 2 x 1 + 3 x 2 − x 1 + x 2 = = = 2 ⋯ ( R 1 ) 4 ⋯ ( R 2 ) 0 ⋯ ( R 3 ) ⇒ ⇒ ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 1 + x 2 − x 1 + x 2 − x 1 + x 2 = = = 2 0 0 ( R 2 − 2 R 1 → R 2 ) ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 1 + x 2 − x 1 + x 2 0 ⋅ x 1 + 0 ⋅ x 2 = = = 2 0 0 ( R 3 − R 2 → R 3 ) 위의 연립방정식은 당연히 x 1 = 1 & x 2 = 1 x_1 = 1 \ \& \ x_2 = 1 x 1 = 1 & x 2 = 1
다시말해, n < m n < m n < m 0 = 0 0 = 0 0 = 0
그럼 존재하지 않는 경우도 살펴보겠습니다.
case2> 존재하지 않는 경우
{ x 1 + x 2 = 3 ⋯ ( R 1 ) x 1 + 2 x 2 = 4 ⋯ ( R 2 ) x 1 − x 2 = − 1 ⋯ ( R 3 ) ⇒ { x 1 + x 2 = 3 x 1 + 2 x 2 = 4 2 x 1 + 0 ⋅ x 2 = 2 ( R 1 + R 3 → R 3 ) ⇒ { x 1 + x 2 = 3 x 1 + 2 x 2 = 4 x 1 + 0 ⋅ x 2 = 1 ( 1 2 R 3 → R 3 ) \begin{matrix} \begin{cases} x_1 + x_2 &=& 3 \ \cdots\ (R_1) \\ x_1 + 2x_2 &=& 4 \ \cdots\ (R_2) \\ x_1 - x_2 &=& -1 \ \cdots\ (R_3) \end{cases} & \Rightarrow & \begin{cases} x_1 + x_2 &=& 3 \\ x_1 + 2x_2 &=& 4 \\ 2x_1 + 0\cdot x_2 &=& 2 \end{cases} \quad (R_1+R_3 \rightarrow R_3) \\ \\ & \Rightarrow & \begin{cases} x_1 + x_2 &=& 3 \\ x_1 + 2x_2 &=& 4 \\ x_1 +0\cdot x_2 &=& 1 \end{cases} \quad ({1 \over 2}R_3 \rightarrow R_3) \end{matrix} ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 1 + x 2 x 1 + 2 x 2 x 1 − x 2 = = = 3 ⋯ ( R 1 ) 4 ⋯ ( R 2 ) − 1 ⋯ ( R 3 ) ⇒ ⇒ ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 1 + x 2 x 1 + 2 x 2 2 x 1 + 0 ⋅ x 2 = = = 3 4 2 ( R 1 + R 3 → R 3 ) ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x 1 + x 2 x 1 + 2 x 2 x 1 + 0 ⋅ x 2 = = = 3 4 1 ( 2 1 R 3 → R 3 ) 그럼 R 1 R_1 R 1 x 1 x_1 x 1 x 2 = 2 x_2 = 2 x 2 = 2 R 2 R_2 R 2 x 1 x_1 x 1 x 2 = 3 2 x_2 = {3\over 2} x 2 = 2 3
3. n = m n = m n = m :n < m n < m n < m n > m n > m n > m
이제 부터는 위의 경우에서 (0 = 0 0 = 0 0 = 0
먼저 연립방정식은 다음과 같이 행렬으로 나타낼 수 있습니다.
Let A be a m × n m \times n m × n x ∈ R n x \in \R^n x ∈ R n y ∈ R m y \in \R^m y ∈ R m
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = y 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = y 2 ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = y m ⇒ [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] [ x 1 x 2 ⋮ x n ] = [ y 1 y 2 ⋮ y m ] ⇒ A x = y \begin{matrix} \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n &=&y_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n &=&y_2 \\ \qquad \qquad \qquad \vdots \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n &=&y_m \end{cases} && \Rightarrow && \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix} \\ \\ && \Rightarrow && Ax = y \end{matrix} ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ a 1 1 x 1 + a 1 2 x 2 + ⋯ + a 1 n x n a 2 1 x 1 + a 2 2 x 2 + ⋯ + a 2 n x n ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = = = y 1 y 2 y m ⇒ ⇒ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ a m 1 a 1 2 a 2 2 ⋮ a m 2 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ a m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 x 2 ⋮ x n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ y 1 y 2 ⋮ y m ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ A x = y 그리고 만약 0 = 0인 항등식이 나오는 경우는 행렬 A A A R i R_i R i linear dependent(선형종속) 이라고 할 수 있습니다.
Def> linear dependent
v 1 , v 2 , ⋯ , v n ∈ R m v_1, v_2, \cdots ,v_n \in \R^m v 1 , v 2 , ⋯ , v n ∈ R m c 1 = c 2 = ⋯ = c n = 0 c_1 = c_2= \cdots =c_n = 0 c 1 = c 2 = ⋯ = c n = 0 ∃ c 1 , c 2 , ⋯ , c n ∈ R such that \exist\ c_1, c_2, \cdots ,c_n \in \R \quad \text{such that} ∃ c 1 , c 2 , ⋯ , c n ∈ R such that
c 1 v 1 + c 2 v 2 + ⋯ + c n v n = 0 ⃗ c_1v_1 + c_2v_2 + \cdots +c_nv_n = \vec0 c 1 v 1 + c 2 v 2 + ⋯ + c n v n = 0 예를 들면 다음과 같습니다.
( i ) v 1 = [ 1 2 3 ] , v 2 = [ − 2 − 4 − 6 ] , v 3 = [ 3 4 5 ] ⇒ 2 v 1 + v 2 + 0 v 3 = 0 ⃗ (\mathbf{i}) \quad v_1 = \begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix} , v_2 = \begin{bmatrix}-2 \\ -4 \\ -6\end{bmatrix} , v_3 = \begin{bmatrix}3 \\ 4 \\ 5\end{bmatrix} \quad \Rightarrow \quad 2v_1 + v_2 + 0v_3 = \vec0 ( i ) v 1 = ⎣ ⎢ ⎡ 1 2 3 ⎦ ⎥ ⎤ , v 2 = ⎣ ⎢ ⎡ − 2 − 4 − 6 ⎦ ⎥ ⎤ , v 3 = ⎣ ⎢ ⎡ 3 4 5 ⎦ ⎥ ⎤ ⇒ 2 v 1 + v 2 + 0 v 3 = 0 ( i i ) v 1 = [ 1 1 0 ] , v 2 = [ − 1 1 1 ] , v 3 = [ − 1 3 2 ] ⇒ v 1 + 2 v 2 − v 3 = 0 ⃗ (\mathbf{ii}) \quad v_1 = \begin{bmatrix}1 \\ 1 \\ 0\end{bmatrix} , v_2 = \begin{bmatrix}-1 \\ 1 \\ 1\end{bmatrix} , v_3 = \begin{bmatrix}-1 \\ 3 \\ 2\end{bmatrix} \quad \Rightarrow \quad v_1 + 2v_2 - v_3 = \vec0 ( i i ) v 1 = ⎣ ⎢ ⎡ 1 1 0 ⎦ ⎥ ⎤ , v 2 = ⎣ ⎢ ⎡ − 1 1 1 ⎦ ⎥ ⎤ , v 3 = ⎣ ⎢ ⎡ − 1 3 2 ⎦ ⎥ ⎤ ⇒ v 1 + 2 v 2 − v 3 = 0 그럼 이와 반대되는 개념인 linear independent(선형독립)은 아래와 같습니다.
Def> linear independent
v 1 , v 2 , ⋯ , v n ∈ R m v_1, v_2, \cdots ,v_n \in \R^m v 1 , v 2 , ⋯ , v n ∈ R m ∄ c 1 , c 2 , ⋯ , c n ∈ R such that \nexists \ c_1, c_2, \cdots ,c_n \in \R \quad \text{such that} ∄ c 1 , c 2 , ⋯ , c n ∈ R such that
c 1 v 1 + c 2 v 2 + ⋯ + c n v n = 0 ⃗ c_1v_1 + c_2v_2 + \cdots +c_nv_n = \vec0 c 1 v 1 + c 2 v 2 + ⋯ + c n v n = 0 즉, 다음과 같은 경우만 위 수식을 만족한다.
c 1 = c 2 = c 3 = ⋯ = c n = 0 c_1 = c_2 = c_3 = \cdots =c_n = 0 c 1 = c 2 = c 3 = ⋯ = c n = 0 지금 까지 선형 연립 방정식에 대한 해를 찾기 위해 다음을 알아보았습니다. 다시 정리하면 다음 사진 같습니다.
R 1 ⋯ R 2 ⋯ ⋮ R m ⋯ [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] [ x 1 x 2 ⋮ x n ] = [ y 1 y 2 ⋮ y m ] \begin{matrix} R_1 \cdots \\ R_2 \cdots \\ \vdots \\ R_m \cdots \\ \end{matrix} \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix} R 1 ⋯ R 2 ⋯ ⋮ R m ⋯ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ a m 1 a 1 2 a 2 2 ⋮ a m 2 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ a m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 x 2 ⋮ x n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ y 1 y 2 ⋮ y m ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
Def> 기본 행 연산(ERO : Elementary Row Operations)
지금 까지 선형 연립 방정식을 해결하기 위해 행을 교환하거나 스칼라를 곱해서 더하거나 하는 연산을 수행해 해를 구했습니다. 기본 행 연산도 이와 같습니다.
기본 행 연산은 3가지 연산이 있습니다. 먼저 행렬 A A A i i i R i R_i R i
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] = [ R 1 R 2 ⋮ R m ] & R i = [ a i 1 a i 2 ⋮ a i n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} \ = \ \begin{bmatrix} R_1 \\ R_2 \\ \vdots \\ R_m \end{bmatrix} \quad \& \quad R_i = \begin{bmatrix} a_{i1} \\ a_{i2} \\ \vdots \\a_{in} \end{bmatrix} A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ a m 1 a 1 2 a 2 2 ⋮ a m 2 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ a m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ R 1 R 2 ⋮ R m ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ & R i = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a i 1 a i 2 ⋮ a i n ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
서로다른 두개의 행 교환하기.
서로 다른 i , j ∈ { 1 , 2 , 3 , ⋯ , m } i, j \in \{1,2,3,\cdots,m\} i , j ∈ { 1 , 2 , 3 , ⋯ , m } R i R_i R i R j R_j R j
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ ⋮ a i 1 a i 2 ⋯ a i n ⋮ ⋮ ⋮ ⋮ a j 1 a j 2 ⋯ a j n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ] = [ R 1 R 2 ⋮ R i ⋮ R j ⋮ R m ] ⇒ R i ⇔ R j [ R 1 R 2 ⋮ R j ⋮ R i ⋮ R m ] = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ ⋮ a j 1 a j 2 ⋯ a j n ⋮ ⋮ ⋮ ⋮ a i 1 a i 2 ⋯ a i n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{in} \\ \vdots & \vdots & \vdots & \vdots \\ a_{j1} & a_{j2} & \cdots & a_{jn} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} \ = \ \begin{bmatrix} R_1 \\ R_2 \\ \vdots \\ R_i \\ \vdots \\ R_j \\ \vdots \\ R_m \end{bmatrix} \Rightarrow^{R_i \Leftrightarrow R_j} \begin{bmatrix} R_1 \\ R_2 \\ \vdots \\ R_j \\ \vdots \\ R_i \\ \vdots \\ R_m \end{bmatrix} \ = \ \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{j1} & a_{j2} & \cdots & a_{jn} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{in} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ a i 1 ⋮ a j 1 ⋮ a m 1 a 1 2 a 2 2 ⋮ a i 2 ⋮ a j 2 ⋮ a m 2 ⋯ ⋯ ⋮ ⋯ ⋮ ⋯ ⋮ ⋯ a 1 n a 2 n ⋮ a i n ⋮ a j n ⋮ a m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ R 1 R 2 ⋮ R i ⋮ R j ⋮ R m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⇒ R i ⇔ R j ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ R 1 R 2 ⋮ R j ⋮ R i ⋮ R m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ a j 1 ⋮ a i 1 ⋮ a m 1 a 1 2 a 2 2 ⋮ a j 2 ⋮ a i 2 ⋮ a m 2 ⋯ ⋯ ⋮ ⋯ ⋮ ⋯ ⋮ ⋯ a 1 n a 2 n ⋮ a j n ⋮ a i n ⋮ a m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
하나의 행에 scalar 곱을 취하기.
임의의 행 R i ( i ∈ { 1 , 2 , 3 , ⋯ , m } ) R_i (i \in\{1,2,3, \cdots, m\}) R i ( i ∈ { 1 , 2 , 3 , ⋯ , m } ) k ∈ R k \in \R k ∈ R
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ ⋮ a i 1 a i 2 ⋯ a i n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ] = [ R 1 R 2 ⋮ R i ⋮ R m ] ⇒ k R i → R i [ R 1 R 2 ⋮ k R i ⋮ R m ] = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ ⋮ k a i 1 k a i 2 ⋯ k a i n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{in} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} \ = \ \begin{bmatrix} R_1 \\ R_2 \\ \vdots \\ R_i \\ \vdots \\ R_m \end{bmatrix} \Rightarrow^{kR_i \rightarrow R_i} \begin{bmatrix} R_1 \\ R_2 \\ \vdots \\ kR_i \\ \vdots \\ R_m \end{bmatrix} \ = \ \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ ka_{i1} & ka_{i2} & \cdots & ka_{in} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ a i 1 ⋮ a m 1 a 1 2 a 2 2 ⋮ a i 2 ⋮ a m 2 ⋯ ⋯ ⋮ ⋯ ⋮ ⋯ a 1 n a 2 n ⋮ a i n ⋮ a m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ R 1 R 2 ⋮ R i ⋮ R m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⇒ k R i → R i ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ R 1 R 2 ⋮ k R i ⋮ R m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ k a i 1 ⋮ a m 1 a 1 2 a 2 2 ⋮ k a i 2 ⋮ a m 2 ⋯ ⋯ ⋮ ⋯ ⋮ ⋯ a 1 n a 2 n ⋮ k a i n ⋮ a m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
하나의 행에 scalar 곱을 한뒤 다른 행과 합치기.
이제 임의의 행 R i R_i R i R i R_i R i R j R_j R j k ∈ R k \in \R k ∈ R i ≠ j i \ne j i = j A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ ⋮ a i 1 a i 2 ⋯ a i n ⋮ ⋮ ⋮ ⋮ a j 1 a j 2 ⋯ a j n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ] = [ R 1 R 2 ⋮ R i ⋮ R j ⋮ R m ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{in} \\ \vdots & \vdots & \vdots & \vdots \\ a_{j1} & a_{j2} & \cdots & a_{jn} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} \ = \ \begin{bmatrix} R_1 \\ R_2 \\ \vdots \\ R_i \\ \vdots \\ R_j \\ \vdots \\ R_m \end{bmatrix} A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ a i 1 ⋮ a j 1 ⋮ a m 1 a 1 2 a 2 2 ⋮ a i 2 ⋮ a j 2 ⋮ a m 2 ⋯ ⋯ ⋮ ⋯ ⋮ ⋯ ⋮ ⋯ a 1 n a 2 n ⋮ a i n ⋮ a j n ⋮ a m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ R 1 R 2 ⋮ R i ⋮ R j ⋮ R m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
⇒ R i + k R j ⇒ R i [ R 1 R 2 ⋮ R i + k R j ⋮ R j ⋮ R m ] = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ ⋮ a i 1 + k a j 1 a i 2 + k a j 2 ⋯ a i n + k a j n ⋮ ⋮ ⋮ ⋮ a j 1 a j 2 ⋯ a j n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 ⋯ a m n ] \Rightarrow^{R_i + kR_j \Rightarrow R_i} \begin{bmatrix} R_1 \\ R_2 \\ \vdots \\ R_i+kR_j \\ \vdots \\ R_j \\ \vdots \\ R_m \end{bmatrix} \ = \ \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{i1}+ka_{j1} & a_{i2}+ka_{j2} & \cdots & a_{in}+ka_{jn} \\ \vdots & \vdots & \vdots & \vdots \\ a_{j1} & a_{j2} & \cdots & a_{jn} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix} ⇒ R i + k R j ⇒ R i ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ R 1 R 2 ⋮ R i + k R j ⋮ R j ⋮ R m ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 ⋮ a i 1 + k a j 1 ⋮ a j 1 ⋮ a m 1 a 1 2 a 2 2 ⋮ a i 2 + k a j 2 ⋮ a j 2 ⋮ a m 2 ⋯ ⋯ ⋮ ⋯ ⋮ ⋯ ⋮ ⋯ a 1 n a 2 n ⋮ a i n + k a j n ⋮ a j n ⋮ a m n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Def> Elementary matrix(기본행렬)
기본행렬이란 항등행렬(identity matrix)에서 한번의 기본 행연산을 수행한 행렬을 말합니다.
예를 들어 I 3 I_3 I 3
I 3 = [ 1 0 0 0 1 0 0 0 1 ] ⇒ { R 1 ⇔ R 3 : [ 0 0 1 0 1 0 1 0 0 ] 3 R 1 → R 1 : [ 3 0 0 0 1 0 0 0 1 ] R 1 − 2 R 3 → R 1 : [ 1 0 − 2 0 1 0 0 0 1 ] I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \quad \Rightarrow \quad \begin{cases} R_1 \Leftrightarrow R_3 \ : \ \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{bmatrix} \\ \\ 3R_1 \rightarrow R_1 \ : \ \begin{bmatrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ \\ R_1 - 2R_3 \rightarrow R_1 \ : \ \begin{bmatrix} 1 & 0 & -2 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{cases} I 3 = ⎣ ⎢ ⎡ 1 0 0 0 1 0 0 0 1 ⎦ ⎥ ⎤ ⇒ ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ R 1 ⇔ R 3 : ⎣ ⎢ ⎡ 0 0 1 0 1 0 1 0 0 ⎦ ⎥ ⎤ 3 R 1 → R 1 : ⎣ ⎢ ⎡ 3 0 0 0 1 0 0 0 1 ⎦ ⎥ ⎤ R 1 − 2 R 3 → R 1 : ⎣ ⎢ ⎡ 1 0 0 0 1 0 − 2 0 1 ⎦ ⎥ ⎤ 또한 일반적인 행렬 A에 기본 행연산을 취하는 것은 기본행렬을 앞에 곱하는 것과 같습니다. 예를 들어 설명해보겠습니다.
크기가 3 × 3 3 \times 3 3 × 3
A = [ 1 2 3 3 1 2 2 1 0 ] A = \begin{bmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \\ 2 & 1 & 0 \\ \end{bmatrix} A = ⎣ ⎢ ⎡ 1 3 2 2 1 1 3 2 0 ⎦ ⎥ ⎤
R 1 ⇔ R 3 R_1 \Leftrightarrow R_3 R 1 ⇔ R 3
A ⇒ R 1 ⇔ R 3 [ 2 1 0 3 1 2 1 2 3 ] = [ 0 0 1 0 1 0 1 0 0 ] [ 1 2 3 3 1 2 2 1 0 ] = E R 1 ⇔ R 3 A A \Rightarrow^{R_1 \Leftrightarrow R_3} \begin{bmatrix} 2 & 1 & 0 \\ 3 & 1 & 2 \\ 1 & 2 & 3 \\ \end{bmatrix} \quad = \quad \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \\ 2 & 1 & 0 \\ \end{bmatrix} \quad = \quad E_{R_1 \Leftrightarrow R_3}A A ⇒ R 1 ⇔ R 3 ⎣ ⎢ ⎡ 2 3 1 1 1 2 0 2 3 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 0 0 1 0 1 0 1 0 0 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 1 3 2 2 1 1 3 2 0 ⎦ ⎥ ⎤ = E R 1 ⇔ R 3 A
3 R 1 → R 1 3R_1 \rightarrow R_1 3 R 1 → R 1
A ⇒ 3 R 1 → R 1 [ 3 6 9 3 1 2 2 1 0 ] = [ 3 0 0 0 1 0 0 0 1 ] [ 1 2 3 3 1 2 2 1 0 ] = E 3 R 1 → R 1 A A \Rightarrow^{3R_1 \rightarrow R_1} \begin{bmatrix} 3 & 6 & 9 \\ 3 & 1 & 2 \\ 2 & 1 & 0 \\ \end{bmatrix} \quad = \quad \begin{bmatrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \\ 2 & 1 & 0 \\ \end{bmatrix} \quad = \quad E_{3R_1 \rightarrow R_1}A A ⇒ 3 R 1 → R 1 ⎣ ⎢ ⎡ 3 3 2 6 1 1 9 2 0 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 3 0 0 0 1 0 0 0 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 1 3 2 2 1 1 3 2 0 ⎦ ⎥ ⎤ = E 3 R 1 → R 1 A
R 3 − 2 R 1 → R 3 R_3 - 2R_1 \rightarrow R_3 R 3 − 2 R 1 → R 3
A ⇒ R 3 − 2 R 1 → R 3 [ 1 2 3 3 1 2 0 − 3 − 6 ] = [ 1 0 0 0 1 0 − 2 0 1 ] [ 1 2 3 3 1 2 2 1 0 ] = E R 3 − 2 R 1 → R 3 A A \Rightarrow^{R_3 - 2R_1 \rightarrow R_3} \begin{bmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \\ 0 & -3 & -6 \\ \end{bmatrix} \quad = \quad \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -2 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \\ 2 & 1 & 0 \\ \end{bmatrix} \quad = \quad E_{R_3 - 2R_1 \rightarrow R_3}A A ⇒ R 3 − 2 R 1 → R 3 ⎣ ⎢ ⎡ 1 3 0 2 1 − 3 3 2 − 6 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 1 0 − 2 0 1 0 0 0 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 1 3 2 2 1 1 3 2 0 ⎦ ⎥ ⎤ = E R 3 − 2 R 1 → R 3 A
이렇게 기본 행연산은 기본행렬을 곱한것과 같습니다.
이제부터는 기본 행연산을 통해 선형연립방정식을 계산하는 방법인 가우스 소거법을 이용한 방법에 대해 살펴보겠습니다.
선형 연립 방정식에서 해 구하기
Let A A A n × n n \times n n × n x , b x, b x , b n n n
A x = b ⇒ [ a 11 a 12 a 13 ⋯ a 1 n a 21 a 22 a 23 ⋯ a 2 n a 31 a 32 a 33 ⋯ a 3 n ⋮ ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 a n 3 ⋯ a n n ] [ x 1 x 2 x 3 ⋮ x n ] = [ b 1 b 2 b 3 ⋮ b n ] ⇒ [ a 11 a 12 a 13 ⋯ a 1 n b 1 a 21 a 22 a 23 ⋯ a 2 n b 2 a 31 a 32 a 33 ⋯ a 3 n b 3 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ a n 1 a n 2 a n 3 ⋯ a n n b n ] \begin{matrix} Ax = b && \Rightarrow && \begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \end{bmatrix} \ = \ \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ \vdots \\ b_n \end{bmatrix} \\ \\ && \Rightarrow && \left[ \begin{array}{ccccc|c} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} & b_2 \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} & b_3 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} & b_n \\ \end{array} \right] \end{matrix} A x = b ⇒ ⇒ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 a 3 1 ⋮ a n 1 a 1 2 a 2 2 a 3 2 ⋮ a n 2 a 1 3 a 2 3 a 3 3 ⋮ a n 3 ⋯ ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n a 3 n ⋮ a n n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 x 2 x 3 ⋮ x n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ b 1 b 2 b 3 ⋮ b n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 a 3 1 ⋮ a n 1 a 1 2 a 2 2 a 3 2 ⋮ a n 2 a 1 3 a 2 3 a 3 3 ⋮ a n 3 ⋯ ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n a 3 n ⋮ a n n b 1 b 2 b 3 ⋮ b n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ 이제 부터 해야할 작업은 a 21 , a 31 , ⋯ , a n 1 a_{21}, a_{31}, \cdots, a_{n1} a 2 1 , a 3 1 , ⋯ , a n 1
다시말해 다음 작업을 수행한다.
{ R 2 − k 2 R 1 → R 2 R 3 − k 3 R 1 → R 3 R 4 − k 4 R 1 → R 4 ⋮ R n − k n R 1 → R n ⇒ [ a 11 a 12 a 13 ⋯ a 1 n b 1 0 a 22 ′ a 23 ′ ⋯ a 2 n ′ b 2 ′ 0 a 32 ′ a 33 ′ ⋯ a 3 n ′ b 3 ′ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 a n 2 ′ a n 3 ′ ⋯ a n n ′ b n ′ ] \begin{matrix} \begin{cases} R_2 &-& k_2R_1 &\rightarrow& R_2 \\ R_3 &-& k_3R_1 &\rightarrow& R_3 \\ R_4 &-& k_4R_1 &\rightarrow& R_4 \\ && \vdots & \\ R_n &-& k_nR_1 &\rightarrow& R_n \end{cases} \quad \Rightarrow \quad \left[ \begin{array}{ccccc|c} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} & b_1 \\ 0 & a^\prime_{22} & a^\prime_{23} & \cdots & a^\prime_{2n} & b^\prime_2 \\ 0 & a^\prime_{32} & a^\prime_{33} & \cdots & a^\prime_{3n} & b^\prime_3 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & a^\prime_{n2} & a^\prime_{n3} & \cdots & a^\prime_{nn} & b^\prime_n \\ \end{array} \right] \end{matrix} ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ R 2 R 3 R 4 R n − − − − k 2 R 1 k 3 R 1 k 4 R 1 ⋮ k n R 1 → → → → R 2 R 3 R 4 R n ⇒ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 0 0 ⋮ 0 a 1 2 a 2 2 ′ a 3 2 ′ ⋮ a n 2 ′ a 1 3 a 2 3 ′ a 3 3 ′ ⋮ a n 3 ′ ⋯ ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ′ a 3 n ′ ⋮ a n n ′ b 1 b 2 ′ b 3 ′ ⋮ b n ′ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ 이런 방식으로 1열의 값을 1행을 제와하고 0으로 만듭니다. 같은방법으로 2열 부터 n열까지 수행합니다.
즉, A A A U U U
⇒ [ u 11 u 12 u 13 ⋯ u 1 n b 1 0 u 22 u 23 ⋯ u 2 n b 2 0 0 u 33 ⋯ u 3 n b 3 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 0 ⋯ u n n b n ] \Rightarrow \qquad \left[ \begin{array}{ccccc|c} u_{11} & u_{12} & u_{13} & \cdots & u_{1n} & b_1 \\ 0 & u_{22} & u_{23} & \cdots & u_{2n} & b_2 \\ 0 & 0 & u_{33} & \cdots & u_{3n} & b_3 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & u_{nn} & b_n \\ \end{array} \right] ⇒ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u 1 1 0 0 ⋮ 0 u 1 2 u 2 2 0 ⋮ 0 u 1 3 u 2 3 u 3 3 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ u 1 n u 2 n u 3 n ⋮ u n n b 1 b 2 b 3 ⋮ b n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ 위와 같이 상삼각행렬을 만들었다면 가우스 소거법은 끝이 나게되고 다시 연립방정식으로 고쳐 해를 구하면 됩니다.
가우스 조르단 소거법에서는 다음과정으로 대각행렬(D D D [ b i ] [b_i] [ b i ]
⇒ [ d 11 0 0 ⋯ 0 b 1 0 d 22 0 ⋯ 0 b 2 0 0 d 33 ⋯ 0 b 3 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 0 ⋯ d n n b n ] \Rightarrow \qquad \left[ \begin{array}{ccccc|c} d_{11} & 0 & 0 & \cdots & 0 & b_1 \\ 0 & d_{22} & 0 & \cdots & 0 & b_2 \\ 0 & 0 & d_{33} & \cdots & 0 & b_3 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & d_{nn} & b_n \\ \end{array} \right] ⇒ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ d 1 1 0 0 ⋮ 0 0 d 2 2 0 ⋮ 0 0 0 d 3 3 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ 0 0 0 ⋮ d n n b 1 b 2 b 3 ⋮ b n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ 위 행렬을 다시 풀면 각각의 변수의 값을 구할 수 있습니다.
Example>
다음과 같은 3차 방정식의 해를 구하여라.
{ 2 x 1 + x 2 + x 3 = 5 4 x 1 − 6 x 2 = − 2 − 2 x 1 + 7 x 2 + 2 x 3 = 9 \begin{cases} 2x_1 + x_2 + x_3 = 5 \\ 4x_1 - 6x_2 = -2 \\ -2x_1 + 7x_2 + 2x_3 = 9 \\ \end{cases} ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 2 x 1 + x 2 + x 3 = 5 4 x 1 − 6 x 2 = − 2 − 2 x 1 + 7 x 2 + 2 x 3 = 9 sol>
{ 2 x 1 + x 2 + x 3 = 5 4 x 1 − 6 x 2 = − 2 − 2 x 1 + 7 x 2 + 2 x 3 = 9 ⇒ [ 2 1 1 5 4 − 6 0 − 2 − 2 7 2 9 ] ⇒ [ 2 1 1 5 0 − 8 − 2 − 12 0 8 3 14 ] ⇒ [ 2 1 1 5 0 − 8 − 2 − 12 0 0 1 2 ] ⇒ [ 2 1 0 3 0 − 8 0 − 8 0 0 1 2 ] ⇒ [ 2 0 0 2 0 − 8 0 − 8 0 0 1 2 ] ⇒ [ 1 0 0 1 0 1 0 1 0 0 1 2 ] \begin{matrix} \begin{cases} 2x_1 + x_2 + x_3 = 5 \\ 4x_1 - 6x_2 = -2 \\ -2x_1 + 7x_2 + 2x_3 = 9 \\ \end{cases} & \Rightarrow & \left[ \begin{array}{ccc|c} 2 & 1 & 1 & 5 \\ 4 & -6 & 0 & -2 \\ -2 & 7 & 2 & 9 \\ \end{array} \right] \\\\ & \Rightarrow & \left[ \begin{array}{ccc|c} 2 & 1 & 1 & 5 \\ 0 & -8 & -2 & -12 \\ 0 & 8 & 3 & 14 \\ \end{array} \right] \\\\ & \Rightarrow & \left[ \begin{array}{ccc|c} 2 & 1 & 1 & 5 \\ 0 & -8 & -2 & -12 \\ 0 & 0 & 1 & 2 \\ \end{array} \right] \\\\ & \Rightarrow & \left[ \begin{array}{ccc|c} 2 & 1 & 0 & 3 \\ 0 & -8 & 0 & -8 \\ 0 & 0 & 1 & 2 \\ \end{array} \right] \\\\ & \Rightarrow & \left[ \begin{array}{ccc|c} 2 & 0 & 0 & 2 \\ 0 & -8 & 0 & -8 \\ 0 & 0 & 1 & 2 \\ \end{array} \right] \\\\ & \Rightarrow & \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 2 \\ \end{array} \right] \end{matrix} ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 2 x 1 + x 2 + x 3 = 5 4 x 1 − 6 x 2 = − 2 − 2 x 1 + 7 x 2 + 2 x 3 = 9 ⇒ ⇒ ⇒ ⇒ ⇒ ⇒ ⎣ ⎢ ⎡ 2 4 − 2 1 − 6 7 1 0 2 5 − 2 9 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 2 0 0 1 − 8 8 1 − 2 3 5 − 1 2 1 4 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 2 0 0 1 − 8 0 1 − 2 1 5 − 1 2 2 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 2 0 0 1 − 8 0 0 0 1 3 − 8 2 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 2 0 0 0 − 8 0 0 0 1 2 − 8 2 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 1 0 0 0 1 0 0 0 1 1 1 2 ⎦ ⎥ ⎤ 그럼 해는 x 1 = 1 , x 2 = 1 , x 3 = 2 x_1 = 1, x_2 = 1, x_3 = 2 x 1 = 1 , x 2 = 1 , x 3 = 2
해를 구하기 위해 기본행 연산이 몇 번 사용했는지 알아보겠습니다.
A → U A \rightarrow U A → U ( n − 1 ) + ( n − 2 ) + ⋯ + 1 = n ( n − 1 ) 2 \ (n-1) + (n-2) + \cdots + 1 = {n(n-1) \over 2} ( n − 1 ) + ( n − 2 ) + ⋯ + 1 = 2 n ( n − 1 )
U → D U \rightarrow D U → D ( n − 1 ) + ( n − 2 ) + ⋯ + 1 = n ( n − 1 ) 2 \ (n-1) + (n-2) + \cdots + 1 = {n(n-1) \over 2} ( n − 1 ) + ( n − 2 ) + ⋯ + 1 = 2 n ( n − 1 )
D → I D \rightarrow I D → I n \ n n
거의 일반적으로 n 2 n^2 n 2
역행렬 구하기
바로 역행렬의 존재성에 대해 설명하겠습니다.
우리는 행렬 A A A I I I
A → E R O I : [ a 11 a 12 a 13 ⋯ a 1 n a 21 a 22 a 23 ⋯ a 2 n a 31 a 32 a 33 ⋯ a 3 n ⋮ ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 a n 3 ⋯ a n n ] → E R O [ 1 0 0 ⋯ 0 0 1 0 ⋯ 0 0 0 1 ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 0 0 ⋯ 1 ] \begin{matrix} A \rightarrow_{ERO} I &:& \begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} \\ \end{bmatrix} & \rightarrow_{ERO} & \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ \end{bmatrix} \end{matrix} A → E R O I : ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ a 1 1 a 2 1 a 3 1 ⋮ a n 1 a 1 2 a 2 2 a 3 2 ⋮ a n 2 a 1 3 a 2 3 a 3 3 ⋮ a n 3 ⋯ ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n a 3 n ⋮ a n n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ → E R O ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 0 0 ⋮ 0 0 1 0 ⋮ 0 0 0 1 ⋮ 0 ⋯ ⋯ ⋯ ⋱ ⋯ 0 0 0 ⋮ 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ 가우스 조르단 방법을 활용해 구할 수 있으며 기본행연산이 n 2 n^2 n 2
( E n 2 … E 1 ) A = I (E_{n^2}\dots E_1 )A = I ( E n 2 … E 1 ) A = I 다시 말해 ( E n 2 … E 1 ) = A − 1 (E_{n^2}\dots E_1) = A^{-1} ( E n 2 … E 1 ) = A − 1
물론 앞서 말한 A A A linear independent 을 만족해야합니다.
만족하지 않을 경우 기본행연산 과정중 0 ⃗ \vec0 0
가우스 조르단 소거법을 활용해서 역행렬을 구할 수 있게되었습니다.
이번 포스팅은 여기서 마치겠습니다. 읽어주셔서 감사합니다. 잘못된 부분이나 궁금한 부분이 있으시면 댓글 부탁드립니다.
Reference