[Platinum I] 큰 수 곱셈 (2) - 15576

문제 링크

성능 요약

메모리: 48496 KB, 시간: 332 ms

분류

고속 푸리에 변환, 수학

제출 일자

2025년 2월 2일 20:08:33

문제 설명

두 정수 A와 B가 주어졌을 때, 두 수의 곱을 출력하는 프로그램을 작성하시오.

입력

첫째 줄에 정수 A와 B가 주어진다. 두 정수는 0보다 크거나 같은 정수이며, 0을 제외한 정수는 0으로 시작하지 않으며, 수의 앞에 불필요한 0이 있는 경우도 없다. 또한, 수의 길이는 300,000자리를 넘지 않는다.

출력

두 수의 곱을 출력한다.

문제 풀이

FFT 공부중입니다. 부족한 부분이나 틀린 부분이 있다면 지적해주세요.

A. 기본 접근 방식
일반적인 O(n²) 곱셈 알고리즘으로는 300,000자리의 곱셈을 2초 안에 처리할 수 없다. 따라서 FFT를 이용한 O(n log n) 알고리즘을 사용한다.

1. 복소수 연산

typedef complex<double> base;
const double PI = acos(-1);

C++의 STL complex 클래스 사용으로 복소수 연산 구현

2. FFT 알고리즘

void fft(vector<base>& a, bool invert) {
    // bit-reversal permutation
    // butterfly operations
    // scaling for inverse FFT
}

문제풀이 구현

1. 수가 크기때문에 문자열로 입력받아 자릿수로 쪼갠다.
2. FFT
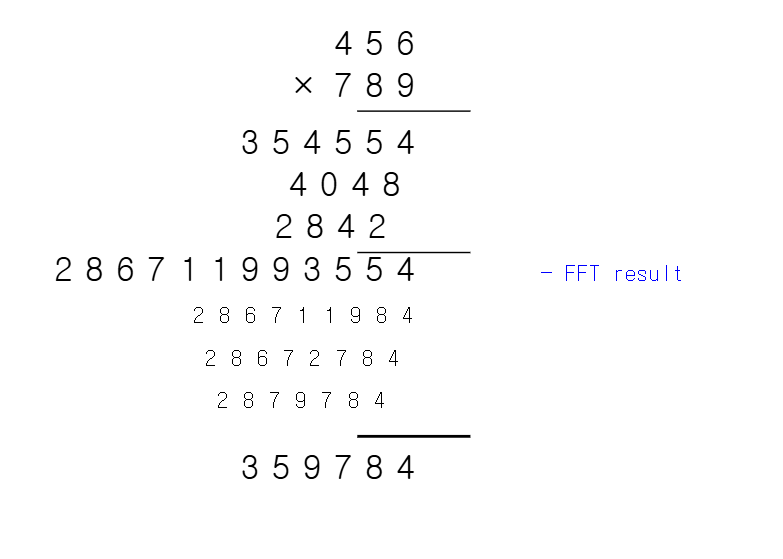
   다항식 곱셈을 위해 내가 공부한 바로는 요약하자면 두 a, b, 다항식을 FFT로 한 뒤 convolution하여 다시 역방향으로 FFT하면 계수가 다 나온다.

fft(fa, false);  // 순방향 FFT
fft(fb, false);
for(int i = 0; i < n; i++)
    fa[i] *= fb[i];  // 점별 곱셈
fft(fa, true);   // 역방향 FFT

3. 결과처리
   각 자릿수이므로 0~9숫자로 만들기. 올림처리도
   

코드

BOJ_15576_큰 수 곱셉 (2)

C++ 코드

/**
 * Author: nowalex322, Kim HyeonJae
 */
#include <bits/stdc++.h>
using namespace std;

// #define int long long
#define MOD 1000000007
#define INF LLONG_MAX
#define ALL(v) v.begin(), v.end()

#ifdef LOCAL
#include "algo/debug.h"
#else
#define debug(...) 42
#endif

typedef complex<double> base;
typedef long long ll;
const double PI = acos(-1);

void fft(vector<base>& a, bool invert) {
    int n = a.size(), j = 0;
    vector<base> roots(n / 2);

    for (int i = 1; i < n; i++) {
        int bit = (n >> 1);
        while (j >= bit) {
            j -= bit;
            bit >>= 1;
        }
        j += bit;
        if (i < j) swap(a[i], a[j]);
    }

    double ang = 2 * PI / n * (invert ? -1 : 1);
    for (int i = 0; i < n / 2; i++) {
        roots[i] = base(cos(ang * i), sin(ang * i));
    }

    for (int i = 2; i <= n; i <<= 1) {
        int step = n / i;
        for (int j = 0; j < n; j += i) {
            for (int k = 0; k < i / 2; k++) {
                base u = a[j + k], v = a[j + k + i / 2] * roots[step * k];
                a[j + k] = u + v;
                a[j + k + i / 2] = u - v;
            }
        }
    }
    if (invert) {
        for (int i = 0; i < n; i++) a[i] /= n;
    }
}

void solve() {
    string s1, s2;
    cin >> s1 >> s2;

    if (s1 == "0" || s2 == "0") {
        cout << "0\n";
        return;
    }

    vector<ll> a(s1.size()), b(s2.size());
    for (int i = 0; i < s1.size(); i++) a[s1.size() - i - 1] = s1[i] - '0';
    for (int i = 0; i < s2.size(); i++) b[s2.size() - i - 1] = s2[i] - '0';

    vector<base> fa(a.begin(), a.end()), fb(b.begin(), b.end());
    int n = 2;
    while (n < a.size() + b.size()) n <<= 1;
    fa.resize(n);
    fb.resize(n);

    fft(fa, false);
    fft(fb, false);
    for (int i = 0; i < n; i++) fa[i] *= fb[i];
    fft(fa, true);

    vector<ll> result(n);
    for (int i = 0; i < n; i++) result[i] = (ll)round(fa[i].real());

    for (int i = 0; i < result.size() - 1; i++) {
        result[i + 1] += result[i] / 10;
        result[i] %= 10;
    }

    int idx = result.size() - 1;
    while (idx > 0 && result[idx] == 0) idx--;
    for (; idx >= 0; idx--) cout << result[idx];
    cout << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int tt = 1;  // 기본적으로 1번의 테스트 케이스를 처리
    // cin >> tt;    // 테스트 케이스 수 입력 (필요 시)

    while (tt--) {
        solve();
    }
    return 0;
}

---

BOJ_22289_큰 수 곱셈 (3)

Java 코드

/**
 * Author: nowalex322, Kim HyeonJae
 */

import java.io.*;
import java.util.*;

public class Main {
    public static class NTT {
        static final long MOD = 998244353;
        static final long PRIMITIVE_ROOT = 3;

        static long pow(long a, long b) {
            long res = 1;
            while (b > 0) {
                if ((b & 1) == 1) {
                    res = res * a % MOD;
                }
                a = a * a % MOD;
                b >>= 1;
            }
            return res;
        }

        static void ntt(long[] a, boolean invert) {
            int n = a.length;

            // bit-reversal permutation
            for (int i = 1, j = 0; i < n; i++) {
                int bit = n >> 1;
                while (j >= bit) {
                    j -= bit;
                    bit >>= 1;
                }
                j += bit;
                if (i < j) {
                    long temp = a[i];
                    a[i] = a[j];
                    a[j] = temp;
                }
            }

            // NTT computation
            for (int len = 2; len <= n; len <<= 1) {
                long wlen = pow(PRIMITIVE_ROOT, (MOD - 1) / len);
                if (invert) {
                    wlen = pow(wlen, MOD - 2);
                }

                for (int i = 0; i < n; i += len) {
                    long w = 1;
                    for (int j = 0; j < len/2; j++) {
                        long u = a[i + j];
                        long v = a[i + j + len/2] * w % MOD;

                        a[i + j] = (u + v) % MOD;
                        a[i + j + len/2] = (u - v + MOD) % MOD;

                        w = w * wlen % MOD;
                    }
                }
            }

            if (invert) {
                long inv_n = pow(n, MOD - 2);
                for (int i = 0; i < n; i++) {
                    a[i] = a[i] * inv_n % MOD;
                }
            }
        }

        static long[] multiply(long[] a, long[] b) {
            int n = 1;
            while (n < a.length + b.length) n <<= 1;

            long[] fa = Arrays.copyOf(a, n);
            long[] fb = Arrays.copyOf(b, n);

            ntt(fa, false);
            ntt(fb, false);

            for (int i = 0; i < n; i++) {
                fa[i] = fa[i] * fb[i] % MOD;
            }

            ntt(fa, true);
            return fa;
        }
    }
    static BufferedReader br;
    static BufferedWriter bw;
    static StringTokenizer st;
    static StringBuilder sb = new StringBuilder();
    public static void main(String[] args) throws Exception {
        new Main().solution();
    }

    public void solution() throws Exception {
        br = new BufferedReader(new InputStreamReader(System.in));
//        br = new BufferedReader(new InputStreamReader(new FileInputStream("src/main/java/BOJ_15576_큰수곱셈2/input.txt")));
        bw = new BufferedWriter(new OutputStreamWriter(System.out));

        st = new StringTokenizer(br.readLine());
        String A = st.nextToken();
        String B = st.nextToken();

        int lenA = A.length();
        int lenB = B.length();
        int maxLen = Math.max(lenA, lenB);

        int n = 1;
        while (n < lenA + lenB - 1) n <<= 1;

        long[] LL_A = new long[n];
        long[] LL_B = new long[n];

        for(int i=0; i<lenA; i++) {
            LL_A[i] = A.charAt(lenA-1-i) - '0';
        }

        for(int i=0; i<lenB; i++) {
            LL_B[i] = B.charAt(lenB-1-i) - '0';
        }

        NTT.ntt(LL_A, false);
        NTT.ntt(LL_B, false);

        for (int i = 0; i < n; i++) {
            LL_A[i] = LL_A[i] * LL_B[i] % NTT.MOD;
        }

        NTT.ntt(LL_A, true);

        long[] res = new long[lenA + lenB];
        for (int i = 0; i < lenA + lenB - 1; i++) {
            res[i] = LL_A[i];
        }

        for (int i = 0; i < lenA + lenB - 1; i++) {
            if (res[i] >= 10) {
                res[i + 1] += res[i] / 10;
                res[i] %= 10;
            }
        }
        boolean leadingZero = true;

        for(int i=res.length-1; i>=0; i--) {
            if(leadingZero && res[i] == 0) continue;
            leadingZero = false;
            sb.append(res[i]);
        }

        if(sb.length()==0) sb.append(0);

        bw.write(sb.toString());
        bw.flush();
        bw.close();
        br.close();
    }
}