[Paper Review]Graph Convolutional Neural Networks for Web-Scale Recommender Systems

(수정중...)

3. Method

3.1. Problem Setup

Pinterest의 목적 : Pin에 대한 Embedding혹은 Representation을 얻는 것.
-> Pinterest를 bipartie graph로 모델링 함.

Node의 종류 : I(Containing Pin), C(Containing Board)
논문에서는 I : Item 집합
C : Context or Collection의 집합

Item은 실수 attrivute와 관련되어 있는것으로 가정함.
=> Raw Feature를 의미 == Item에 대한 메타데이터나 컨텐츠 정보를 의미

Goal : input attributes 사이에 높은 질의 bipartie graph 구조를 이용해서 양질의 embedding을 만드는 것

Final Embedding은 Nearest Neighbor Lookup을 통해 Candidate Generation형태로 활용하거나 Candidate에 랭킹을 매기는 머신러닝 시스템에서의 Feature형태로 활용될 것 임.

전체 그래프의 노드 집합은 V = I ∪ C로 사용. 반드시 필요한 경우가 아니면, Pin과 board node를 구분하지 않고 그냥 node라는 용어를 사용함.

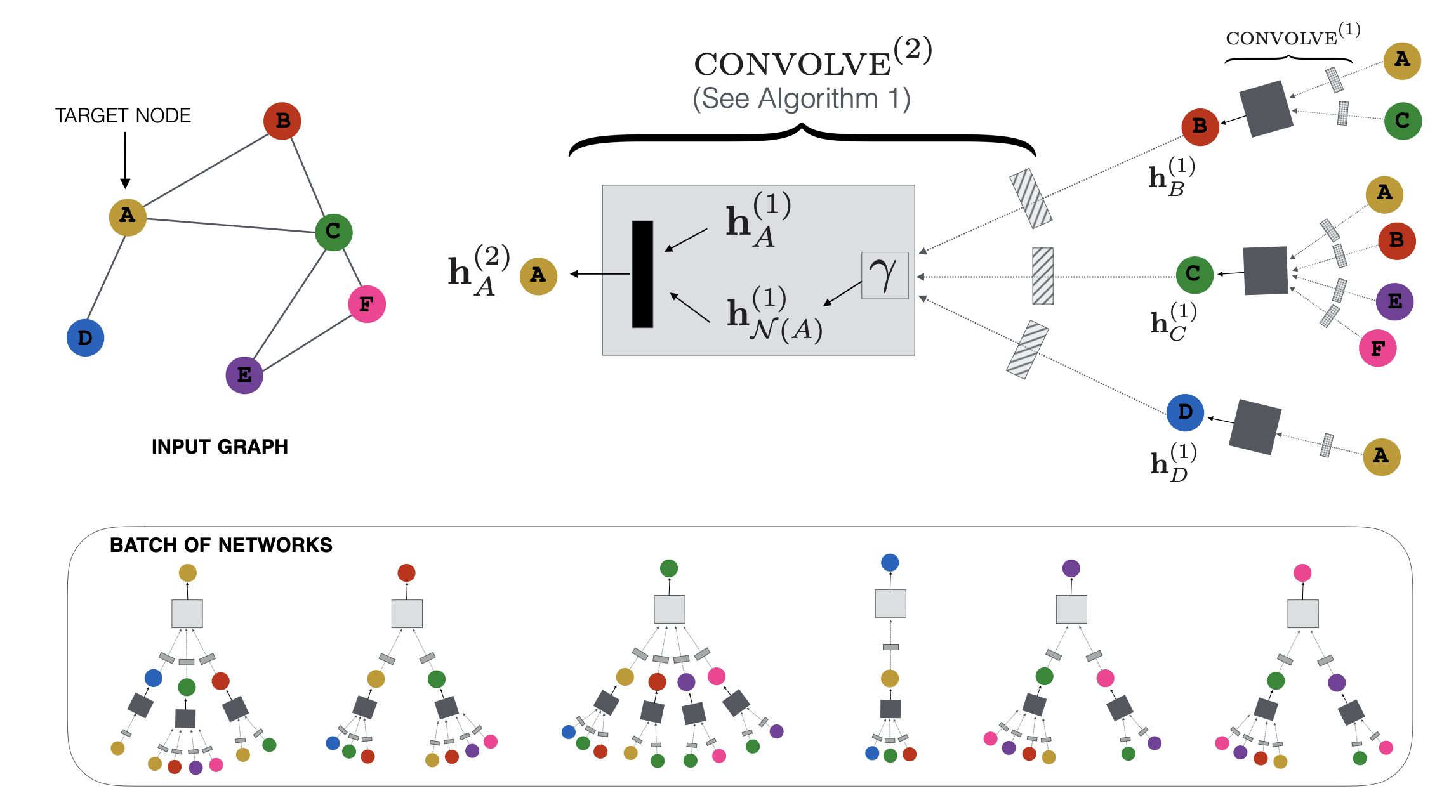
3.2 Model Architecture

노드 임베딩을 생성하기 위해 localized convolutional modules을 사용함
input node의 feature를 시작으로 graph에서 feature를 변환하고 aggregate하는 NN을 학습하여 node embedding을 계산함.

Forward Propagation algorithm

z_u를 생성하는 작업을 고려하는데, node의 input feature과 이 node 주변의 graph structure에 의존함

PinSage 알고리즘의 핵심 : localized convolution operation
u는 이웃으로부터 정보를 aggregate하는 방법을 학습함.

Importance-based neighborhoods

PinSage에서 중요점
node의 Neighbor을 어떻게 정의할지가 중요함.
즉 이웃집합 N(u)의 셋을 선택하는 방법이 중요함.

GCN에서는 그냥 k-hop의 이웃을 aggregate했는데, PinSage에서는 중요도 기반으로 이웃을 정의한다. Sampling하는 측면에서 Graph Sage와 비슷한것 같음.

이때 노드 u의 이웃은 가장 큰 영향을 미치는 T개의 노드로 정의 함.
노드 u를 시작으로 하는 randomwalk를 하고, 가장 많이 방문한 노드 중 상위 T개의 노드로 정의함.

중요도를 기반으로한 importance based neighborhood definition의 장점
1. 집계할 노드의 고정된 수를 선택하면 training할 때 알고리즘의 메모리 사용량을 줄일 수 있음.
2. 알고리즘1이 neighborhood의 중요성을 고려해서 aggregate할 수 있게 함.

특히 알고리즘 1에서 γ를 L1 norm의 방문횟수에 따라 정의된 가중치를 가진 weighted average로 구현함. => importance pooling

Stacking convolutions

알고리즘 1을 적용할 때마다 노드에 대한 새로운 표현을 얻게 됨. => 합성곱을 여러번 쌓아서 노드 u의 주변 로컬 그래프 구조에 대한 정보를 더 많이 얻을 수 있음

k-th layer에서의 input은 (k-1)-th layer의 output이 들어감.
initial input은 input node의 feature과 같음

알고리즘 1에서의 parameter(Q,q,W,w)는노드간에 공유되는데, layer간에는 공유되지 않음.

알고리즘 2 : 스택된 합성곱이 노드 미니 배치 세트 M의 임베딩 생성법을 설명함.

각 노드의 neighborhood를 계산후 K번의 합성곱 반복을 적용해서 대상 노드의 k-th layer의 representation을 생성함.
convolutional layer의 final output은 fc layer을 통해 final output으로 만들어짐.

전체 매개변수 세트는 각 합성곱 계층의 가중치와 치와 바이어스 매개변수(Q^(k), q^(k), W^(k), w^(k), ∀k ∈ {1, ...,K})와 최종 밀집 신경망 계층의 매개변수인 G1, G2, g를 학습함.

알고리즘 1의 1행에서의 ouput의 dimension은 m인데, 간소화를 위해 모든 합성곱 계층의 output dimension은 동일하게 설정하고 parameter로 d로 표시함.
모델의 final output의 dimension도 d로 설정함.

3.3 Model Training

max-margin ranking loss를 이용해서 PinSage를 학습시킴. 라벨링 된 아이템 쌍의 집합을 L이라고 했을때, 집합 내의 쌍 (q,i) ∈ L은 관련이 있다고 가정한다.
=> (q,i) ∈ L이면 아이템 i는 쿼리 아이템 q에 대한 좋은 추천 후보라고 가정한다.

훈련 단계에서는 라벨링된 (q,i) ∈ L의 출력 임베딩이 가까워 지도록 PinSage 매개변수를 최적화 한다.

Loss function

max-margin-based loss function을 사용함.
positive example의 쿼리 아이템의 임베딩과 관련 아이템의 임베딩을 최대화 하는 것. 동시에 negative example의 내적, 즉 쿼리 아이템의 임베딩과 관련 없는 아이템의 임베딩 사이의 내적이 positive example보다 일정하게 정이 된 margin만큼 작도록 한다.

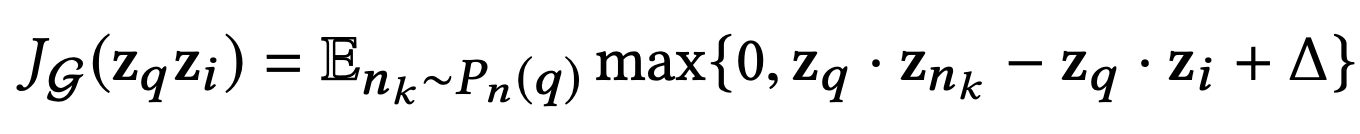
P_n(q)는 아이템 q에 대한 negative example의 distribution임
∆는 margin hyper-parameter를 나타냄.

Sampling negative items

loss function에서 negative sampling이 edge likelihood의 정규화 인자의 근사치로 사용됨.
각 미니배치에서 모든 훈련 예시에 공유될 500개의 negative item을 sampling 함. => 각 훈련 단계에서 계산해야 할 임베딩의 수를 줄임.각 node마다 negative sampling을 하는것과 비교했을 때, 성능 차이는 없다. 근데 계산은 적게 한다.그러나 이런 것들은 너무 쉬움.

특히 PinSage는 20억개가 넘는 카탈로그 중 q와 가장 관련있는 1,000개의 아이템을 찾을 수 있어야 함. 근데 500개의 random negative item은 쿼리 아이템과 관련 있을 확률이 너무 낮음. 따라서 조금 관련된 아이템과 많이 관련된 아이템을 구별할 수 없다.

이런 문제를 해결하기 위해, 이 논문에서는 'hard'negative example, 즉 쿼리 아이템 q와 어느정도 관련 있지만 positive item i만큼은 아닌 아이템을 추가 함.

=> 쿼리 아이템 q에 대한 개인화된 pagerank score에 따라 그래프에서 아이템을 순위 매기는 것으로 생성됨.
2000-5000위에 순위된 아이템들이 random hard negative item으로 sampling 됨.

=> hard random negative item은 일반적인 random negative example보다 쿼리 q와 더 유사한 것(즉 Query Item과 어느정도 관련은 있는데, positive example만큼 관련있지는 않은 item을 추가 한 것)을 추가헤준다고 생각하면 될 것 같음.

이렇게 hard random negative item을 사용하면 일반적인 상황보다 훈련이 수렴하는 데 필요한 epoch의 수가 2배가 필요하다.
따라서 curriculum training scheme을 개발했다.
첫번째 epoch에서는 hard negative items를 넣지 않고 학습한다. 이 후 각 Query Item마다 1개의 hard negative items를 추가함.
=> Epoch이 하나씩 지날 수록 hard negative items가 1개씩 더 추가 됨.

Node Embeddings via MapReduce