Automated Essay Scoring via Pairwise Contrastive Regression

https://aclanthology.org/2022.coling-1.240/
https://github.com/CarryCKW/AES-NPCR

Abstract

자동 에세이 채점(AES)은 에세이의 작문 품질과 관련된 점수를 예측하는 것을 포함합니다. AES에 관한 대부분의 기존 연구들은 각각 회귀 목적 또는 랭킹 목적을 활용합니다. 그러나 이 두 가지 유형의 방법은 상호 보완성이 높습니다. 이를 위해, 본 논문에서는 대조 학습(contrastive learning)에서 영감을 받아 두 목적 함수가 단일 손실(loss)로 동시에 최적화되는 새로운 통합 신경망 쌍별 대조 회귀(NPCR) 모델을 제안합니다. 구체적으로, 우리는 먼저 대규모 에세이 목록에서 전역적인 랭킹 순서를 보장하기 위해 신경망 쌍별 랭킹 모델을 설계하고, 그다음 이 쌍별 랭킹 모델을 확장하여 입력 에세이와 여러 참조 에세이 간의 상대 점수를 예측합니다. 추가적으로, 추론 시에는 다중 샘플 투표 전략이 사용됩니다. 우리는 공개 Automated Student Assessment Prize (ASAP) 데이터셋에서 모델을 평가하기 위해 이차 가중 카파(Quadratic Weighted Kappa)를 사용하며, 실험 결과는 NPCR이 이전 방법들을 큰 차이로 능가하여 AES 작업에 대한 SOTA(state-of-the-art) 평균 성능을 달성함을 보여줍니다.

1. 소개

자동 에세이 채점(AES)은 컴퓨터 기술을 사용하여 에세이의 품질을 평가하고 자동으로 점수를 매기는 것입니다. 주목할 점은, 합리적인 채점은 많은 시간과 인적 노력을 요구하는 문제를 해결할 수 있다는 것입니다. 더욱이, 학습자에게 피드백을 제공하는 것은 자기 계발을 촉진할 수 있습니다. 이는 자연어 처리(NLP)의 가장 중요한 응용 분야 중 하나이며 교육 분야에서 널리 요구됩니다.

대부분의 기존 방법들은 일반적으로 AES를 회귀(regression) 작업으로 재구성하며, 그 목표는 에세이의 점수를 예측하는 것입니다 (Taghipour and Ng, 2016; Dong and Zhang, 2016; Dong et al., 2017; Tay et al., 2018). 몇 가지 유망한 결과가 달성되었음에도 불구하고, 이러한 회귀 기반 모델은 훈련 데이터의 레이블링 정보를 효율적이고 직접적으로 활용하지 못합니다. 게다가, 또 다른 연구 흐름은 AES를 학습-투-랭크(learning-to-rank) 방법을 사용한 선호도 랭킹 문제로 취급합니다. Yannakoudakis 등 (2011)은 특징 추출을 통해 문서 쌍의 순위를 매기는 것을 처음 제안했습니다; 이후, Chen and He (2013)는 이 작업을 리스트 단위(listwise) 랭킹 문제로 변환했습니다. Cummins 등 (2016) 또한 동일한 프롬프트에서 나온 두 에세이의 순위를 매기기 위해 전이 학습(transfer learning)을 수행했습니다.

그러나 AES에 관한 대부분의 기존 연구들은 각각 회귀 목적 또는 랭킹 목적을 활용합니다. 사실, 이 두 가지 유형의 방법은 상호 보완성이 높습니다. 한편으로, AES에 회귀 모델만을 사용하는 것은 훈련 데이터 내 에세이 간의 점수 관계를 명시적으로 모델링할 수 없습니다. 다른 한편으로, 랭킹 기반 모델만을 사용하는 것은 정확한 점수를 보장할 수 없습니다. 실제로, 교사가 학생의 에세이를 평가하고 채점할 때, 일반적으로 먼저 하나 또는 여러 개의 모범 에세이를 참조로 비교한 다음 특정 점수를 부여합니다.

최근 Yang 등 (2020)은 간단한 동적 결합 전략을 사용하여 회귀 손실과 랭킹 손실을 공동으로 최적화하는 다중 손실(multi-loss) 방법을 적용함으로써 AES 작업에서 회귀와 랭킹을 결합한 첫 번째 연구를 발표했습니다. 그럼에도 불구하고, 두 최적화 목적 함수 간의 균형(tradeoff)을 달성하기 위한 결합 가중치를 결정하는 것은 실제로 상당히 어렵습니다. 게다가, 제안된 배치 단위(batch-wise) 학습 기반 랭킹 모델은 정확성을 희생하며 각 배치 내의 에세이 순위만 매깁니다.

위의 문제들을 해결하기 위해, 본 논문에서는 회귀 목적과 랭킹 목적이 동시에 최적화되는 AES 작업을 위한 통합 프레임워크를 탐색하며, 이는 두 가지 대중적인 AES 솔루션의 장점을 통합하는 것을 목표로 합니다. 여기서 핵심 과제는 두 개의 상당히 다른 최적화 목적 함수를 단일 손실을 가진 단일 모델로 통합하는 방법입니다. 이를 위해, 우리는 대조 학습(contrastive learning) (Yu et al., 2021; Chen et al., 2020)에서 영감을 받아, 두 목적 함수를 원칙적인 방식으로 공동 최적화하는 새로운 통합 신경망 쌍별 대조 회귀(NPCR) 모델을 제안합니다. 간단히 말해, 대조 학습의 목표는 더 나은 표현 공간(representation space)을 학습하는 것입니다 (Chen et al., 2020). 특히, 주어진 두 에세이에 대해, 동일한 범주의 유사한 에세이 간의 거리는 작아야 하고, 유사하지 않은 에세이 간의 거리는 커야 하며, 이러한 의미 관계는 표현 공간에서의 거리 측정을 통해 반영될 수 있습니다. 따라서, 대조 학습 프레임워크 하에서, 제안하는 모델은 입력 에세이를 표현 공간으로 매핑하고 상대 점수를 통해 에세이 간의 차이를 계산하는 것을 목표로 합니다. 구체적으로, 우리는 먼저 대규모 에세이 목록에서 전역적인 랭킹 순서를 보장하기 위해 신경망 쌍별 랭킹 모델을 설계하고, 그다음 이 신경망 쌍별 랭킹 모델을 확장하여 입력 에세이와 여러 참조 에세이 간의 상대 점수를 예측합니다. 추가적으로, 모든 입력 테스트 에세이에 대한 추론을 위해 다중 샘플 투표 전략이 채택됩니다.

우리는 Automated Student Assessment Prize (ASAP) 데이터셋에서 모델을 평가하기 위해 이차 가중 카파(Quadratic Weighted Kappa)를 사용하며, 실험 결과는 제안하는 모델이 이전 방법들을 큰 차이로 능가하며 이 공개 벤치마크에서 새로운 SOTA(state-of-the-art)를 확립함을 보여줍니다.

요약하자면, 본 연구의 기여는 다음과 같이 결론지을 수 있습니다: (1) 우리가 아는 한, 회귀 및 랭킹 최적화를 동시에 수행하는 AES 작업을 위한 통합 프레임워크를 탐색한 첫 번째 시도입니다; (2) 우리는 대규모 에세이 목록에서 전역적인 랭킹 순서를 보장하는 AES를 위한 신경망 쌍별 랭킹 모델을 제안합니다; (3) 공개 데이터셋 ASAP에서의 실험 결과는 제안하는 접근 방식이 SOTA 평균 성능을 달성할 뿐만 아니라, 거의 모든 프롬프트에서 모든 베이스라인에 비해 더 나은 성능을 얻음을 보여줍니다.

2. 배경

2.1 과제 설명

자동 에세이 채점 시스템은 주어진 프롬프트에 따라 작성된 학생 에세이를 평가하고 채점하는 데 사용됩니다. 이러한 시스템의 성능은 시스템이 에세이 집합에 할당한 점수를 사람이 할당한 정답(gold standard) 점수와 비교하여 평가됩니다. AES 시스템의 출력은 일반적으로 실수 값(real-valued number)이므로, 이 작업은 종종 지도 기계 학습 작업(주로 회귀 또는 선호도 랭킹)으로 다루어집니다.

2.2 회귀와 랭킹의 결합을 위한 다중 손실 방법

회귀 손실과 랭킹 손실의 상호 보완성을 활용하기 위해, Yang 등 (2020)은 수식 1과 같은 간단한 동적 최적화 전략을 사용하여 AES 작업을 위한 BERT 모델을 미세 조정(fine-tune)하기 위한 다중 손실 목적 함수를 제안합니다. 그러나 두 손실 간의 균형을 달성하기에 적합한 결합 가중치를 결정하는 것은 매우 어렵습니다.

$L = \tau_{e} L_{m} + (1 - \tau_{e}) L_{r} \quad (1)$

여기서 $L_{m}$은 회귀 목적 함수이고, $L_{r}$은 배치 단위(batchwise) 손실 함수의 결과이며, $\tau_{e}$는 에포크 수에 따라 변하는 파라미터입니다.

게다가, Yang 등 (2020)은 매번 에세이 목록의 순위를 매기고 예측된 랭킹 리스트와 실제 정답 레이블 간의 정확도를 측정하는 배치 단위 접근 방식인 ListNet을 사용합니다. 이 방법의 주요 결함은 배치 내의 에세이 순위만 매길 수 있으며 정확한 전역 순서(global order)를 보장할 수 없다는 것입니다.

3. AES를 위한 쌍별 대조 회귀

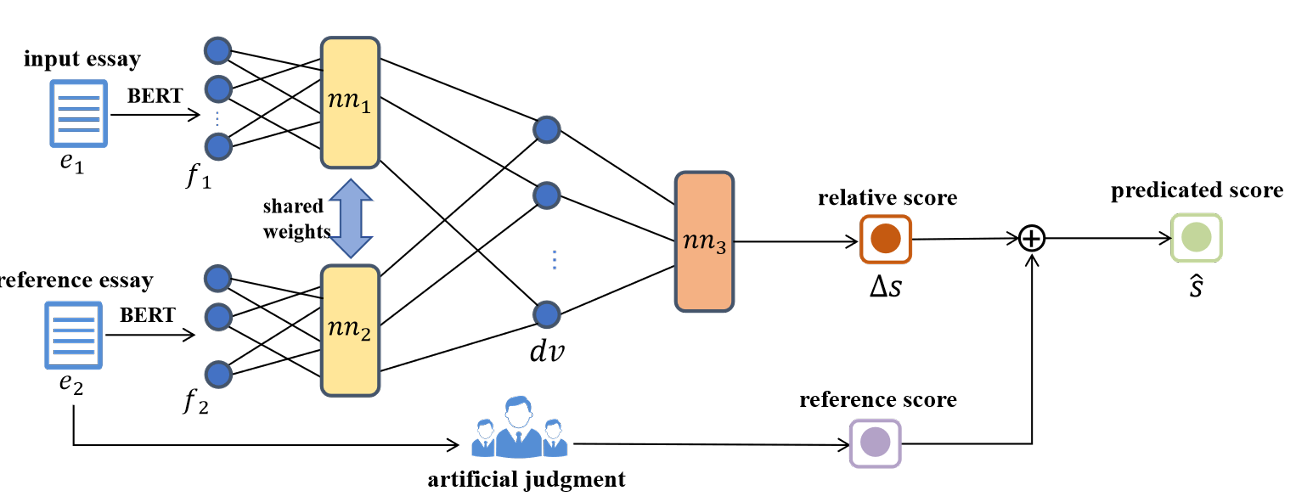
Figure 1: The overall framework of neural pairwise contrastive regression model for AES

3.1 방법론 개요

전통적으로, 대부분의 기존 연구들은 AES를 회귀 작업으로 공식화합니다. 여기서 입력은 에세이이고 출력은 해당 에세이의 작문 품질과 관련된 예측 점수입니다 (Taghipour and Ng, 2016; Dong and Zhang, 2016; Tay et al., 2018).

공식적으로, 점수 레이블 $s$를 가진 입력 에세이 $e$가 주어졌을 때, 회귀 문제는 입력 에세이의 품질에 기반하여 점수 $\hat{s}$를 예측하는 것입니다:

$\hat{s} = R_{\theta}(F_{W}(e)) \quad (2)$

여기서 $R_{\theta}$와 $F_{W}$는 각각 $\theta$와 $W$로 파라미터화된 회귀 모델(regressor)과 특징 추출기(feature extractor)입니다.

그림 1: AES를 위한 신경망 쌍별 대조 회귀 모델의 전체 프레임워크.

그러나 회귀 목적 함수만 최적화하는 것은 훈련 데이터의 점수 레이블 정보를 잘 활용하기에 부적절합니다. 반면에, 랭킹 기반 방법은 에세이 간의 점수 관계를 명시적으로 모델링할 수 있습니다 (Yannakoudakis et al., 2011). 따라서, 이 두 가지 방법의 상호 보완성을 활용하기 위해, 우리는 AES 문제를 입력과 모범 답안(exemplar) 간의 상대 점수를 회귀하는 것으로 재공식화할 것을 제안합니다.

$e_{i}$를 입력 에세이, $e_{j}$를 점수 레이블 $s_{j}$를 가진 참조 에세이라고 할 때, 이 회귀 문제는 다음과 같이 다시 작성될 수 있습니다:

$\hat{s}_{i} = R_{\theta}(F_{W}(e_{i}, e_{j})) + s_{j} \quad (3)$

여기서 목표는 상대 점수, 즉 입력 에세이와 참조 에세이 간의 점수 차이를 예측하는 것임에 유의해야 합니다.

기술적으로 말해서, 상대 점수를 성공적으로 예측하는 데 있어 주요 과제는 단일 에세이가 아닌 에세이 쌍(pair)을 입력으로 받는 효과적인 회귀 모델을 설계하는 방법에 있습니다. 단일 에세이 입력과는 대조적으로, 에세이 쌍을 입력으로 받는 이 회귀 모델은 반사성(reflexivity) 및 반대칭성(antisymmetry)과 같은 더 많은 특성을 만족해야 합니다.

이를 달성하기 위해, 우리는 상대 점수를 예측하는 AES용 신경망 쌍별 대조 회귀 모델을 제안합니다. 우리 방법의 전체적인 프레임워크는 그림 1에 나와 있습니다. 방법론적으로, 우리의 쌍별 대조 회귀 모델은 사실 AES를 위한 신경망 쌍별 랭커(ranker)의 자연스러운 확장입니다.

우리의 접근 방식을 명확하게 설명하기 위해, 다음 하위 섹션에서는 먼저 AES를 위한 신경망 쌍별 랭커의 설계를 자세히 소개한 다음, 이 목표를 달성하기 위해 이를 쌍별 대조 회귀 모델로 더욱 확장합니다.

3.2 AES를 위한 신경망 쌍별 학습-투-랭크

이 섹션에서는 DirectRanker (Köppel et al., 2019)에 동기를 부여받아, 대규모 에세이 목록이 주어졌을 때 전역적인 랭킹 순서를 예측하는 AES용 신경망 쌍별 랭킹 모델을 설계하는 것을 목표로 합니다. 이를 위해, 임의의 두 에세이 $e_{1}$과 $e_{2}$가 주어졌을 때, $e_{1}$이 $e_{2}$보다 더 높은 점수를 갖도록 하는 부분 순서 연산자(partial order operator) $e_{1} \ge e_{2}$를 먼저 정의합니다. 일관되고 전역적인 순서를 달성하기 위해, 이 연산자는 반사성(reflexivity), 반대칭성(antisymmetry), 추이성(transitivity)이라는 세 가지 특성을 만족해야 합니다.

나아가, 우리는 이 연산자를 구현하기 위해 특징 공간 $\mathcal{F}$ 상의 랭킹 함수 $rf: \mathcal{F} \times \mathcal{F} \rightarrow \mathcal{R}$를 사용합니다:

$x \ge y : \Leftrightarrow rf(x, y) \ge 0, \quad \text{for } x, y \in \mathcal{F} \quad (4)$

따라서, 이 연산자의 세 가지 특성은 함수 $rf$를 통해 다음과 같이 정의될 수 있습니다:

(A) 반사성: $rf(x, x) = 0$
(B) 반대칭성: $rf(x, y) = -rf(y, x)$
(C) 추이성: $(rf(x, y) \ge 0 \wedge rf(y, z) \ge 0) \Rightarrow rf(x, z) \ge 0$

특히, 이러한 요구 사항을 충족시키기 위해 랭킹 함수 $rf$는 특정 구조를 가진 신경망을 사용하여 구현될 수 있습니다.

첫째로, 입력 에세이 $e$를 저차원 벡터 공간으로 매핑하기 위해, 풍부한 의미 정보를 완전히 활용할 수 있는 BERT (Devlin et al., 2019)를 사용하여 텍스트 벡터 표현 $f$를 얻습니다:

$h = BERT(e) \in \mathcal{R}^{r_{h} \times |e|} \quad (5)$
$f = h_{[CLS]} \quad (6)$

여기서 $h$는 은닉 표현(hidden representations), $r_{h}$는 은닉 상태(hidden state)의 차원, $|e|$는 입력 에세이의 길이를 나타냅니다. 특별한 토큰 [CLS]에 매핑되는 은닉 표현인 벡터 $f$는 입력 에세이 $e$의 텍스트 표현으로 사용됩니다.

다음으로, 그림 1에서 볼 수 있듯이, 모델의 특징 추출 부분은 다층 퍼셉트론(multi-layer perceptron)으로 구성된 두 개의 서브넷 $nn_{1}$과 $nn_{2}$를 포함합니다. 두 서브넷은 가중치, 편향, 활성화 함수 등 동일한 구조와 파라미터를 공유합니다. 그런 다음 두 서브넷 $nn_{1}$과 $nn_{2}$의 두 출력값 간의 차이 벡터 $dv$는 다음과 같이 간단히 계산될 수 있습니다:

$dv = F_{w}(f_{1}) - F_{w}(f_{2}) \quad (7)$

여기서 $f_{1}$과 $f_{2}$는 한 에세이 쌍의 표현 벡터이고, $F_{w}$는 $w$로 파라미터화된 특징 추출기입니다.

그 후, 차이 벡터 $dv$는 단 하나의 출력 뉴런을 가진 세 번째 서브넷 $nn_{3}$에 입력됩니다. (Köppel et al., 2019)에 의해 보여진 바와 같이, 반대칭 활성화 함수(antisymmetric activation functions)를 선택하고 뉴런의 편향(bias)을 제거함으로써 반대칭성을 쉽게 보장할 수 있습니다.

사실, 위의 세 가지 특성이 우리 모델에서 만족될 수 있음을 증명하는 것은 쉽습니다. 더 구체적으로, 우리는 먼저 반대칭 활성화 함수를 정의하기 위해 사용합니다. 즉, $\phi: \mathcal{R} \rightarrow \mathcal{R}$에 대해 $\phi(-x) = -\phi(x)$입니다.

(I) (II)의 만족은 (I)이 추론될 수 있음을 의미합니다.
$rf(x, x) = -rf(x, x) \Rightarrow rf(x, x) \equiv 0 \quad (8)$

(II) 위에서 언급했듯이, $nn_{1}$과 $nn_{2}$는 일관된 네트워크 구조를 가지므로, 동일한 함수 $g: \mathcal{F} \rightarrow \mathcal{R}^{n}$를 사용합니다. 따라서, 두 입력 특징 벡터 $x, y \in \mathcal{F}$에 대해, (B)는 다음과 같이 증명될 수 있습니다:

$rf(x,y) = \phi[w(g(x)-g(y))] = -\phi[wg(y)-wg(x)] = -rf(y,x) \quad (9)$

여기서 $w$는 가중치 벡터입니다.

(III) $x, y, z \in \mathcal{F}$이고, $rf(x, y) \ge 0$ 이고 $rf(y, z) \ge 0$이라고 가정할 때, 모델의 추이성은 다음과 같이 증명될 수 있습니다:

$rf(x,z) = \phi[w(g(x)-g(z))] = \phi[wg(x)-wg(y)+wg(y)-wg(z)] = rf(x,y)+rf(y,z) \ge 0 \quad (10)$

여기서 $w$는 가중치 벡터이고 $g$는 (II)에서 정의된 바와 같습니다. 따라서, (C)를 준수합니다.

3.3 AES를 위한 쌍별 대조 회귀 모델

다음으로, 이전 섹션에서 설명한 신경망 쌍별 랭킹 모델을 확장하여 입력 에세이와 참조 에세이 간의 상대 점수를 예측하는 쌍별 대조 회귀 모델을 형성합니다. 사실, 이를 달성하는 것은 비교적 간단합니다.

쌍별 랭킹 모델로서, 그림 1에 표시된 세 번째 서브넷 $nn_{3}$의 출력은 단지 이진(binary) 값입니다. 만약 이 서브넷의 출력 값이 상대 점수에 해당하는 실수 값이 되도록 허용하고 두 번째 입력 에세이를 참조 샘플로 지정한다면, 변환된 모델은 사실상 기본적인 대조 회귀 모델입니다.

그런 다음, 차이 벡터 $dv$는 반대칭 활성화 함수를 가지고 편향이 없는 단 하나의 출력 뉴런으로 구성된 완전 연결 신경망(fully connected neural network)에 입력됩니다.

차이 벡터 $dv$가 주어졌을 때, 쌍별 대조 모델은 다음과 같이 간단히 정의될 수 있습니다:

$\Delta s = R_{\theta}(dv) \quad (11)$

여기서 $\Delta s$는 임의의 두 에세이 간의 상대 점수를 나타내고 $\theta$는 회귀 모델의 파라미터입니다.

이 상대 점수의 회귀 문제는 훈련 데이터에 대한 예측된 상대 점수와 실제(golden) 상대 점수를 기반으로 계산될 수 있는 평균 제곱 오차(MSE) 손실을 최소화함으로써 해결될 수 있습니다. 이 쌍별 대조 회귀에 해당하는 손실 함수는 다음과 같습니다:

$L_{r} = \frac{1}{N} \sum_{i=1}^{N} (\Delta s_{i} - \Delta s_{i}')^2 \quad (12)$

여기서 $N$은 총 에세이 쌍의 수를, $\Delta s_{i}$와 $\Delta s_{i}'$는 각각 예측된 상대 점수와 실제(golden) 상대 점수를 나타냅니다.

원칙적으로, 이 대조 회귀 모델은 반사성, 반대칭성, 그리고 축적성(accumulation)이라는 세 가지 특성을 만족해야 합니다. 구체적으로, 축적성은 다음과 같이 정의될 수 있습니다:

$rf(x, y) + rf(y, z) = rf(x, z) \quad (13)$

분명히, 반사성과 반대칭성은 모두 이전 섹션과 동일한 신경망 아키텍처를 채택함으로써 쉽게 만족될 수 있습니다. 그럼에도 불구하고, 이론적으로, 이 대조 회귀 모델에서의 축적성은 어떤 신경망 모델 자체에 의해서도 보장될 수 없습니다. 따라서, 이 대조 회귀 모델의 학습 목표 중 하나는 축적성을 가능한 한 많이 충족시키는 것입니다.

이러한 관점에서 볼 때, 훈련 중에 에세이 쌍을 선택하는 방법이 중요해집니다. 따라서 우리는 훈련 데이터를 구성하기 위한 효과적인 선택 전략을 설계합니다. 특히, 우리는 먼저 각 프롬프트의 모든 에세이를 훈련 데이터에 나타나는 순서대로 시퀀스로 배열한 다음, 시퀀스에서 인접한 두 에세이를 순서대로 골라 하나의 쌍으로 만듭니다. 더욱이, 축적성의 필요를 충족시키기 위해 중요한 추가 단계가 부과됩니다. 구체적으로, 만약 우리가 $(e_{i}, e_{j})$와 $(e_{j}, e_{k})$ 에세이 쌍을 훈련 인스턴스로 선택한다면, 학습된 모델이 축적성을 만족하도록 하기 위해 $(e_{i}, e_{k})$ 쌍 또한 훈련 데이터에 추가해야 합니다. 추가적으로, 입력 에세이와 참조 에세이를 비교 가능하게 만들기 위해, 우리는 입력 에세이와 동일한 프롬프트를 공유하는 에세이를 참조로 선택하는 경향이 있습니다.

3.4 추론

추론 시에는, 다중 샘플 투표 전략을 사용합니다. 직관적으로, 선택된 참조 샘플은 입력 테스트 에세이와 비교 가능해야 합니다. 그러나, 우리 데이터셋에는 8개의 프롬프트가 있으며, 프롬프트마다 상대 점수 범위가 다릅니다. 위의 문제를 해결하기 위해, 우리는 입력 에세이와 동일한 프롬프트를 가진 일부 샘플 에세이를 선택합니다.

구체적으로, 입력 에세이 $e_{test}$가 주어지면, 훈련 데이터셋에서 $M$개의 샘플을 선택하여, 점수가 $\{s_{train}\}_{m=1}^{M}$인 $M$개의 서로 다른 샘플 $\{e_{train}^{m}\}_{m=1}^{M}$을 사용하여 $M$개의 쌍을 구성합니다. 그러면 $M$개의 예측 점수를 얻게 되며, 입력 에세이의 최종 점수는 이 $M$개 점수의 평균이 됩니다. 다중 샘플 투표 과정은 다음과 같이 요약될 수 있습니다:

$\hat{s}_{test}^{m} = R_{\theta}(F_{w}(e_{test}, e_{train}^{m})) + s_{train}^{m} \quad (14)$

$\hat{s}_{test} = \frac{1}{M} \sum_{m=1}^{M} \hat{s}_{test}^{m} \quad (15)$

여기서 $\theta$와 $w$는 쌍별 대조 회귀 모델의 파라미터입니다. $\hat{s}_{test}^{m}$은 m번째 예측 점수를 나타내고 $\hat{s}_{test}$는 입력 에세이 $e_{test}$의 최종 예측 점수를 나타냅니다.

표 1: ASAP 데이터셋의 상세 정보.

Prompt ID	Essay Set Size	Original Score Range	Relative Score Range
1	1783	2-12	-10-10
2	1800	1-6	-5-5
3	1726	0-3	-3-3
4	1772	0-3	-3-3
5	1805	0-4	-4-4
6	1800	0-4	-4-4
7	1569	0-30	-30-30
8	723	0-60	-60-60

4. 실험

4.1 실험 설정

4.1.1 데이터셋

우리는 실험 평가를 위해 널리 사용되는 ASAP (Automated Student Assessment Prize) 데이터셋을 사용합니다. 이는 William and Flora Hewlett Foundation (Hewlett)에 의해 조직되고 후원된 대회에서 비롯되었습니다. 이 데이터셋은 표 1에 설명된 바와 같이 8개의 프롬프트를 포함하며, 장르와 에세이 수가 각기 다릅니다. 이전 연구를 따라, 우리도 모델 평가를 위해 5-겹 교차 검증(5-fold cross-validation)을 활용합니다. 각 실행에서, 우리는 (Taghipour and Ng, 2016)에 의해 제공된 대로 각 프롬프트에 대한 데이터셋의 60%, 20%, 20%를 각각 훈련 데이터, 검증 데이터, 테스트 세트로 사용합니다.

4.1.2 평가 지표

본 논문에서는, 인간이 채점한 점수(artificial scores)와 예측 결과 간의 일치도를 측정하기 위해 일반적으로 사용되는 지표인 이차 가중 카파(QWK)를 사용합니다. 특히, 에세이 집합이 1에서 $N$까지의 척도로 채점되고, 전문가의 점수가 $i$이고 모델의 예측 점수가 $j$라고 가정합니다.

$K = 1 - \frac{\sum_{i,j} w_{i,j} O_{i,j}}{\sum_{i,j} w_{i,j} E_{i,j}} \quad (16)$
$w_{i,j} = \frac{(i-j)^2}{(N-1)^2} \quad (17)$

여기서 $w, O, E$는 각각 가중치, 관측된 점수, 기대 점수의 행렬입니다. 나아가, $O_{i,j}$의 값은 인간 채점자로부터 $i$점을 받고 AES 시스템으로부터 $j$점을 받은 에세이의 수를 나타냅니다. 그리고 $E_{i,j}$는 점수들의 두 히스토그램 벡터 간의 외적(outer product)을 나타냅니다.

표 2: ASAP 데이터셋에 대한 QWK 평가 점수, 베이스라인 결과는 원본 논문에서 가져옴.

Model	1	2	3	4	5	6	7	8	Avg
EASE(SVR)	0.781	0.630	0.621	0.749	0.782	0.771	0.727	0.534	0.699
EASE(BLRR)	0.761	0.621	0.606	0.742	0.784	0.775	0.730	0.617	0.705
ALL-MTL-CТАР (2016)	0.816	0.667	0.654	0.783	0.801	0.778	0.787	0.692	0.747
CNN+LSTM (2016)	0.821	0.688	0.694	0.805	0.807	0.819	0.808	0.644	0.761
LSTM-CNN-attent (2017)	0.822	0.682	0.672	0.814	0.803	0.811	0.801	0.705	0.764
SKIPFLOW (2018)	0.832	0.684	0.695	0.788	0.815	0.810	0.800	0.697	0.764
HISK+BOSWE (2018)	0.845	0.729	0.684	0.829	0.833	0.830	0.804	0.729	0.785
R2BERT (2020)	0.817	0.719	0.698	0.845	0.841	0.847	0.839	0.744	0.794
NPCR	0.856	0.750	0.756	0.851	0.847	0.858	0.838	0.779	0.817

4.1.3 구현 세부 사항

이전 연구(Yang et al., 2020)를 따라, 우리도 공정한 비교를 위해 $BERT_{base}$ 모델을 사용합니다. 토큰화(tokenization)와 어휘(vocabulary)를 위해, 우리는 모두 BERT 모델에서 제공하는 전처리 도구를 사용합니다. GPU 메모리 제한으로 인해, 에세이의 최대 길이를 512 단어로 설정하고 배치 크기는 5로 설정합니다. 모델을 80 에포크 동안 훈련하고 검증 세트에서의 성능을 기반으로 최상의 모델을 선택합니다. 모델 훈련을 위해 AdamW를 옵티마이저로 사용하며, 초기 학습률(learning rate)은 $1e-5$로 설정합니다. 또한, 훈련 중 모든 상대 점수를 [0,1] 범위로 정규화하고, 평가 시에는 점수를 원래 점수 범위로 다시 조정(rescale)합니다. 이전 연구를 따라, 우리는 프롬프트별(prompt-specific) 방식으로 평가를 수행합니다.

4.2 전체 성능

이 섹션에서는, ASAP 데이터셋에서 평가된 다음과 같은 SOTA(state-of-the-art) 관련 방법들과 우리의 전체적인 성능을 포괄적으로 비교합니다.

4.2.1 베이스라인

• EASE: 우리가 비교하는 주요 비-딥러닝 시스템은 EASE (Enhanced Al Scoring Engine)입니다. 이 시스템은 공개적으로 이용 가능하며 ASAP 대회에서도 우수한 결과를 달성했습니다. 이전 연구들을 따라, EASE의 결과를 서포트 벡터 회귀(SVR) 및 베이지안 선형 리지 회귀(BLRR) 설정으로 보고합니다.
• ALL-MTL-CTAP: Cummins 등 (2016)은 에세이의 표현을 얻기 위해 제한된 다중 작업 쌍별-선호도 학습(constrained multi-task pairwise-preference learning) 방법을 사용했습니다.
• CNN+LSTM: Taghipour and Ng (2016)는 단어 시퀀스 모델링을 위해 CNN을, 텍스트 수준 모델링을 위해 LSTM을 사용하는 신경망 모델을 처음 설계했습니다. 그런 다음, 시간 풀링(mean of time pooling)을 통해 에세이 표현을 얻습니다.
• LSTM-CNN-attent: Dong 등 (2017)은 문장과 문서에서 특징을 추출하기 위해 어텐션 메커니즘을 갖춘 계층적 신경망(hierarchical neural networks) 사용을 제안했습니다.
• SKIPFLOW: Tay 등 (2018)은 예측을 향상시키기 위해 종단간(end-to-end) 신경망 프레임워크의 맥락 내에서 신경망 일관성 특징(neural coherence features)을 고려하는 모델을 제안했습니다.
• HISK+BOSWE: Cozma 등 (2018)은 더 많은 의미적 특징을 추출하기 위해 문자열 커널(string kernels)과 단어 임베딩(word embeddings)을 결합했으며, 도메인 내(in-domain) 및 교차 도메인(cross-domain) 설정 모두에서 더 높은 성능을 얻었습니다.
• R2BERT: Yang 등 (2020)은 AES 작업에서 회귀와 랭킹을 결합하고 BERT 모델을 미세 조정하기 위해 다중 손실 방법을 사용한 첫 번째 연구를 발표했습니다.

4.2.2 성능 비교

표 2는 우리 모델과 위의 SOTA AES 모델들 간의 전체 성능 비교를 보여줍니다. 표 2에서, 우리의 접근 방식이 최고의 베이스라인인 $R^{2}BERT$에 비해 평균 QWK 점수를 2.3% 크게 향상시키는 것을 볼 수 있습니다. 주목할 점은 우리 모델이 SOTA 평균 성능을 달성할 뿐만 아니라, 거의 모든 프롬프트에서 모든 베이스라인에 비해 더 나은 성능을 얻는다는 것이며, 이는 AES를 위해 제안된 쌍별 대조 회귀 모델의 우수성을 보여줍니다.

표 3: 우리 모델에서 회귀 및 랭킹 목적 함수의 사용에 대한 Ablation 연구.

Model	Avg QWK
R2BERT-RegrOnly	0.768
NPCR-RegrOnly	0.770
R2BERT-RankOnly	0.756
NPCR-RankOnly	0.796
NPCR	0.817

표 4: 훈련 및 추론 중 참조 에세이 선택에 대한 성능 비교.

Model	Avg QWK
NPCR-Accu	0.800
NPCR-Group	0.802
NPCR	0.817

그림 2: 참조 에세이의 수에 따라 변하는 성능 곡선.

4.3 분석

4.3.1 대조 회귀 학습의 효과

AES를 위한 이전의 회귀 기반 모델들과 달리, 우리의 접근 방식은 회귀와 랭킹을 대조 회귀 프레임워크 내에서 통합합니다. 이 섹션에서는, ablation test를 통해 대조 회귀를 활용하는 효과를 평가합니다.

표 3의 첫 번째 행에 표시된 바와 같이, 비교를 위해 두 개의 베이스라인이 제시됩니다. 첫 번째 베이스라인 R2BERT-RegrOnly는 R2BERT (Yang et al., 2020)의 회귀 전용(regression only) 버전을 의미합니다. 다른 한편으로, 우리는 NPCR에서 대조 학습 부분을 제거한, 우리 모델 NPCR의 회귀 전용 버전인 두 번째 베이스라인 NPCR-RegrOnly도 구현합니다. 더 구체적으로, 우리는 먼저 BERT를 사용하여 입력 에세이의 표현을 얻은 다음, 시그모이드(sigmoid) 활성화 함수가 있는 완전 연결 레이어를 사용하여 점수를 예측합니다.

표 3의 결과는, 두 베이스라인과 비교할 때, 우리의 전체 모델 NPCR이 QWK 점수를 각각 4.9%와 4.7%씩 일관되게 향상시킴을 보여주며, 이는 우리 모델에 대한 대조 회귀 학습의 중요성을 명확하게 나타냅니다.

4.3.2 쌍별 랭킹의 효과

이 섹션에서는, 우리의 신경망 쌍별 랭킹 모델의 효과를 검토합니다. 표 3의 두 번째 행에서, 첫 번째 베이스라인 $R^{2}$-RankOnly는 $R^{2}$ (Yang et al., 2020)의 랭킹 전용(ranking only) 버전을 의미합니다. 유사하게, 우리는 NPCR에서 점수 예측 부분을 제거한, 우리 모델 NPCR의 랭킹 전용 버전인 두 번째 베이스라인 NPCR-RankOnly도 구현합니다. 세부적으로, NPCR-RankOnly의 출력 레이블은 임의의 두 에세이 간의 우선순위 관계를 나타내는 이진(binary) 값입니다.

추론 시, NPCR-RankOnly는 다중 샘플 투표 전략을 적용하지 않으며, 이는 $M$이 1로 설정됨을 의미합니다. 표 3의 결과를 관찰한 후, 우리는 다음 두 가지 함의를 추론할 수 있습니다: 첫째, NPCR-RankOnly의 성능이 $R^{2}$-RankOnly보다 4.0% 더 좋으며, 이는 우리의 신경망 쌍별 랭킹 방법이 (Yang et al., 2020)의 신경망 배치 단위(batchwise) 기반 랭킹 모델보다 우수함을 보여줍니다. 둘째, 우리의 전체 모델 NPCR과 베이스라인 NPCR-RankOnly 간의 큰 격차는 두 방법의 상호 보완성을 명확하게 보여줍니다.

4.3.3 훈련 샘플 쌍 선택 전략의 효과

우리 모델 NPCR의 축적성을 만족시키기 위해, 3.3절에서 설명한 바와 같이 효과적인 훈련 데이터셋 구축을 위한 샘플 선택 전략을 제안합니다. 이 섹션에서는, 이 샘플 선택 전략의 효과를 검토합니다.

비교를 위해, 훈련 샘플 쌍을 선택할 때 축적성을 고려하지 않는 베이스라인 NPCR-Accu도 구현합니다. 즉, 주어진 에세이 시퀀스에서 인접한 두 에세이만 훈련 데이터셋에 추가됩니다. 표 4의 결과는 NPCR의 평균 QWK 점수가 베이스라인 NPCR-Accu보다 1.7% 더 좋음을 보여줍니다.

4.3.4 참조 에세이 선택 전략의 효과

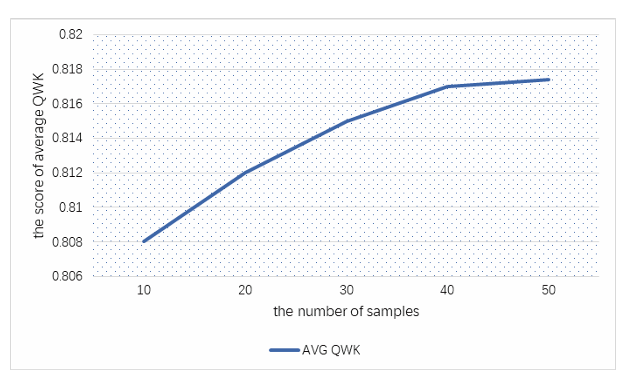
Figure 2: The performance curve varying with different number of reference essays.

추론을 위한 다중 샘플 투표 전략에서 숫자 $M$을 선택하는 것이 필요합니다. 이 섹션에서는, 예측 성능과 참조 에세이 수 간의 관계를 조사합니다.

그림 2는 참조 에세이의 수를 다르게 하여 예측한 결과를 보여줍니다. 그림 2의 성능 곡선은 $M$의 수가 증가함에 따라 성능이 점진적으로 향상되다가, $M$이 40보다 클 때 성능 성장이 수렴하는 경향을 보임을 나타냅니다.

나아가, 우리는 서로 다른 샘플 점수 분포의 영향을 고려하고, 이를 검증하기 위해 그룹-테스팅(group-testing) 전략을 고안합니다. 구체적으로, 우리는 먼저 훈련 에세이의 점수 범위를 겹치지 않는 $M$개의 구간(‘그룹’이라 칭함)으로 나눈 다음, 각 그룹에서 하나의 에세이만 선택하여 $M$개의 참조 에세이를 선택합니다. 표 4에서 우리는 NPCR이 그룹-테스팅 전략을 사용하는 NPCR-Group보다 더 나은 성능을 보임을 알 수 있으며, 이는 무작위로 샘플을 선택하는 것이 서로 다른 점수 그룹에서 샘플을 선택하는 것보다 낫다는 것을 나타냅니다.

그림 3: 프롬프트 1에서 NPCR 및 NPCR-Group 모델에 대한 상대 점수 분포 히스토그램 및 가우시안 커널 밀도 추정.

자세한 이유를 알기 위해, 우리는 참조 에세이 선택 전략에 따른 데이터 분포의 특성을 연구하기 위해, 모든 데이터셋의 훈련 및 테스트 에세이 쌍에 대해 (예: 그림 3의 프롬프트 1) 상대 점수 분포 히스토그램을 생성하고 가우시안 커널 밀도 추정치를 관찰합니다. 우리는 NPCR이 NPCR-Group보다 훈련 데이터와 테스트 데이터의 상대 점수 분포에 대해 더 나은 일관성을 가짐을 발견할 수 있습니다.

4.3.5 여러 사전 훈련된 언어 모델 비교

표 5: 여러 사전 훈련된 언어 모델의 성능 비교.

Model	Avg QWK
NPCR-XLNet	0.816
NPCR-BERT	0.817
NPCR-ROBERTa	0.817

이 섹션에서는 BERT, XLNet, ROBERTa를 포함한 여러 주요 사전 훈련된 언어 모델에 따른 성능 변화를 조사합니다. 표 5의 실험 결과는, 우리 접근 방식에서 기반이 되는 사전 훈련된 언어 모델을 변경할 때 성능이 거의 일정하게 유지됨을 보여주며, 이는 대조 회귀 학습 프레임워크 하의 우리 AES 모델 NPCR이 사전 훈련된 언어 모델의 선택에 비교적 둔감하다는 것을 나타냅니다.

4.3.6 계산 비용

이 섹션에서는, NPCR 모델의 계산 비용을 분석합니다. 단일 에세이를 처리하는 이전 연구와 비교할 때, 우리 모델 NPCR은 실제로 약간 더 많은 계산 비용을 필요로 합니다. 그러나, 우리 모델 NPCR에서, 에세이 쌍을 처리하는 런타임은 베이스라인에서 단일 에세이를 처리하는 비용과 거의 유사하므로, 계산 비용 증가의 한계로 이어집니다. 따라서, 에세이 쌍의 수는 계산 비용을 분석하는 데 중요한 요소입니다.

요약하자면, 훈련 중, 훈련 데이터셋의 에세이 수가 $n$이라면, NPCR에서 계산해야 할 에세이 쌍의 수는 $2 \times n$ 미만입니다; 추론 중, 테스트 세트의 에세이 수가 $n$이라면, NPCR에서 확인해야 할 에세이 쌍의 수는 $M \times n$이 되어야 합니다. 여기서 $M$은 참조 에세이의 수입니다. 실제로, GPU RTX3090Ti로 프롬프트 1에서 NPCR 모델의 실행 시간을 기록했을 때, 평균 훈련 런타임은 에포크 당 90초였으며, 평균 추론 런타임은 40개의 에세이 쌍 당 0.7초였습니다.

5. 관련 연구

자동 에세이 채점 시스템은 수십 년 전부터 중요한 평가(high-stakes assessment)를 위해 배포되어 왔습니다. AES를 위한 초기 접근 방식은 주로 수동으로 설계된 특징(handcrafted feature) 기반 방법(Larkey, 1998; Chodorow and Burstein, 2004; Phandi et al., 2015; Zesch et al., 2015)을 포함했지만, 최근 연구들은 이 작업을 위해 SOTA 성능을 제공하는 딥러닝 기반 방법들을 탐구해 왔습니다.

최근 몇 년간, AES 방법의 주류는 일반적으로 AES를 회귀 작업으로 공식화합니다. AES를 위한 여러 딥러닝 아키텍처 기반 회귀 모델이 제안되었습니다. Taghipour and Ng (2016)는 AES를 위한 첫 번째 신경망 모델을 제시합니다. 이 모델은 먼저 CNN과 LSTM의 조합을 사용하여 에세이의 특징을 추출하여 텍스트 표현 벡터를 생성한 다음, 시그모이드 활성화 함수가 있는 선형 레이어를 적용하여 벡터를 유효한 점수로 매핑합니다. Dong and Zhang (2016)은 단어 수준과 문장 수준에서 자동으로 특징을 학습하기 위해 계층적 구조를 사용합니다. Dong 등 (2017)은 모델에 어텐션 메커니즘을 추가로 도입하고, CNN이 지역적 특징(local features)을 얻는 데 더 도움이 되는 반면, LSTM은 전역적 특징(global features)을 얻는 데 더 적합하다는 것을 증명합니다. Tay 등 (2018)은 종단간(end-to-end) 신경망 프레임워크 내에서 예측을 위한 보조 특징으로 신경망 일관성 특징(neural coherence features)을 고려할 것을 제안합니다. BERT (Devlin et al., 2019) 모델의 최근 발전은 연구자들이 AES에서 사전 훈련된 언어 모델을 사용하도록 영감을 주었습니다 (Rodriguez et al., 2019; Mim et al., 2019; Song et al., 2020).

또 다른 연구 흐름은 AES 작업에 학습-투-랭크(learning-to-rank) 방법을 적용하는 데 중점을 둡니다. Yannakoudakis 등 (2011)은 AES를 랭크 선호도 문제로 처음 공식화한 다음, 통계적 특징을 기반으로 둘 이상의 에세이 순위를 매기기 위해 쌍별 랭킹 모델 RankSVM을 사용합니다. Chen and He (2013)는 언어적 특징(linguistic features)을 기반으로 랭킹 모델을 학습하기 위해 리스트 단위(listwise) 랭킹 방법을 추가로 활용합니다. Cummins 등 (2016)은 각 프롬프트를 서로 다른 작업으로 취급하고 제한된 선호도-랭킹 접근 방식을 도입함으로써 프롬프트 적응(prompt adaptation) 문제를 해결하기 위해 다중 작업 학습(multi-task learning)을 사용합니다.

최근, 랭킹과 회귀 접근 방식의 상호 보완성을 고려하여, Yang 등 (2020)은 간단한 동적 결합 전략을 통해 AES 작업에서 회귀와 랭킹을 결합하는 다중 손실 방법을 제안합니다.

6. 결론

본 논문에서는, 두 가지 대중적인 AES 솔루션의 장점을 통합하는 것을 목표로, 회귀와 랭킹 목적 함수를 원칙적인 방식으로 결합하는 AES를 위한 새로운 통합 모델 NPCR을 제안합니다. 우리의 접근 방식은 개념적으로 간단하지만, 공개 데이터셋 ASAP에서의 실험 결과는 NPCR이 이전 접근 방식들을 상당히 능가하며 AES 작업에서 SOTA(state-of-the-art)를 한 단계 발전시켰음을 보여줍니다.

향후 연구에서는, 문서의 계층적 구조, 일관성 특징 등과 같이 입력 에세이로부터 더 강력한 텍스트 특징을 학습할 수 있도록, 쌍별 대조 회귀 프레임워크 하에서 더 정교한 신경망 특징 추출기를 탐색할 것입니다.