Regress, Don't Guess -- A Regression-like Loss on Number Tokens for Language Models

https://arxiv.org/abs/2411.02083

Abstract

언어 모델은 텍스트 생성에 있어 뛰어난 능력을 가지고 있지만, 숫자를 출력하는 데 대한 자연스러운 귀납적 편향이 부족하여 양적 추론, 특히 산술과 관련된 작업에서 어려움을 겪습니다. 한 가지 근본적인 한계는 명목 척도를 가정하여 생성된 숫자 토큰 간의 근접성을 전달할 수 없는 교차 엔트로피(CE) 손실 함수의 본질에 있습니다. 이에 대한 대응으로, 저희는 순전히 토큰 수준에서 작동하는 회귀와 유사한 손실 함수를 제시합니다. 저희가 제안하는 숫자 토큰 손실(NTL)은 두 가지 종류가 있으며, 실제 숫자 토큰과 예측된 숫자 토큰의 수치 값 사이의 $L_p$ 노름(norm) 또는 바서슈타인(Wasserstein) 거리를 최소화합니다. NTL은 모든 언어 모델에 쉽게 추가될 수 있으며, 런타임 오버헤드 없이 훈련 중에 교차 엔트로피(CE) 목표를 확장할 수 있습니다.

저희는 제안된 방식을 다양한 수학 데이터셋에서 평가했으며, 수학 관련 작업에서 일관되게 성능을 향상시키는 것을 발견했습니다. 회귀 작업에 대한 직접적인 비교에서는, NTL이 토큰 수준에서 작동함에도 불구하고 회귀 헤드(regression head)의 성능과 필적할 수 있음을 확인했습니다. 마지막으로, 저희는 NTL을 30억(3B) 파라미터 모델까지 확장하여 향상된 성능을 관찰했으며, 이를 통해 LLM에 원활하게 통합될 수 있는 잠재력을 입증했습니다.

저희는 이 연구가 LLM 개발자들이 사전 훈련 목표를 개선하도록 영감을 주고, NTL을 미니멀하고 가벼운 PyPI 패키지 ntloss로 배포하기를 희망합니다. 논문 전체 재현을 위한 개발 코드는 별도로 제공됩니다.

---

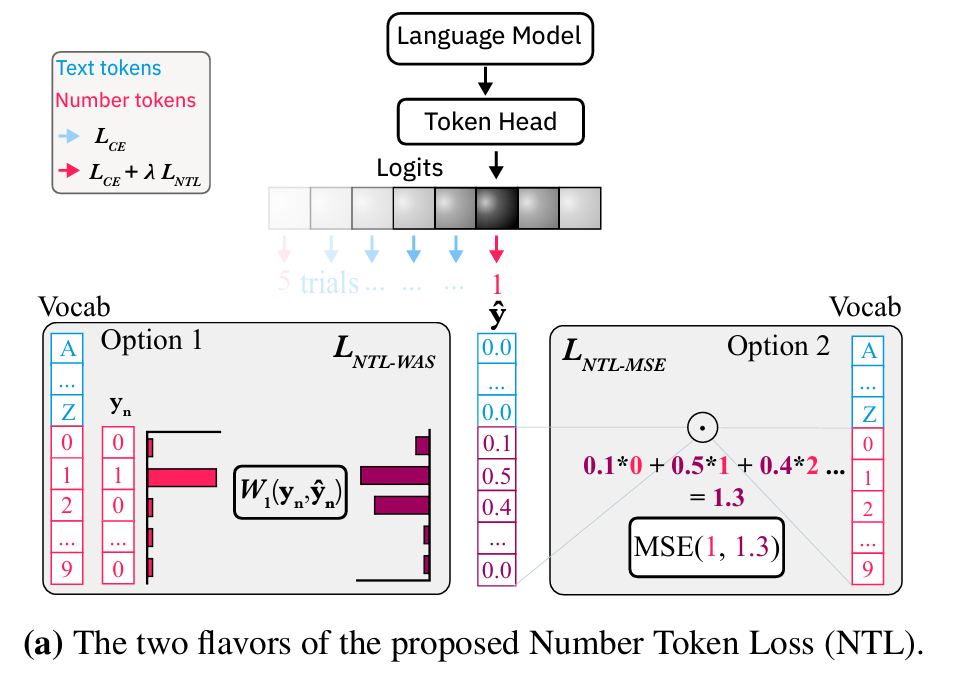
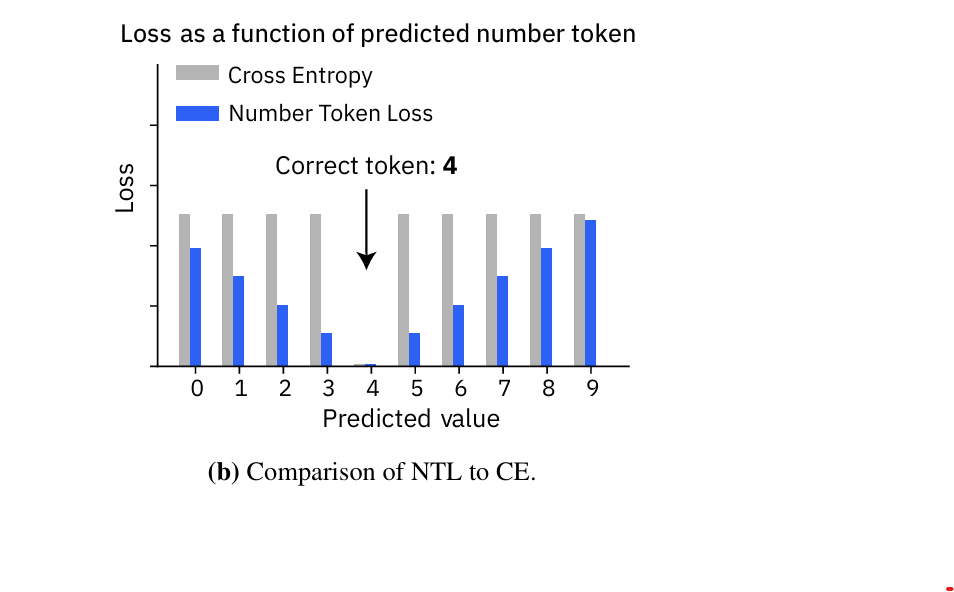
그림 1. (a) 숫자 토큰 손실 (NTL). NTL은 언어 모델링 헤드에서 직접 회귀와 유사한 손실을 계산할 수 있게 해줍니다. 저희는 두 가지 방식을 제안합니다: $\mathcal{L}_{\text{NTL-MSE}}$는 숫자 토큰 값과 그 확률의 내적(dot product)을 사용하고, $\mathcal{L}_{\text{NTL-WAS}}$는 정답(label)과 예측 분포 간의 바서슈타인-1(Wasserstein-1) 거리를 사용합니다. (b) 교차 엔트로피(CE)는 명목 척도이므로 모든 잘못된 예측에 동일한 손실을 할당하는 반면, NTL은 회귀 손실처럼 정답(ground truth)과의 거리가 멀어질수록 손실이 증가합니다.

---

1. Introduction

Thawani et al. (2021)이 언급했듯이, 자연어 텍스트의 숫자는 어디에나 존재하며 중요하지만, 언어 모델(LM)에게는 체계적으로 무시되어 왔습니다. 설상가상으로, 트랜스포머(Vaswani et al., 2017)는 본래 자연어 처리(NLP)를 위해 개발되었지만, 이제는 다양한 과학 분야(Jumper et al., 2021; Boiko et al., 2023)로 확산되었습니다. 이러한 분야들은 NLP보다 표 형식이나 수치 데이터가 더 일반적이며, 종종 과제를 정의하는 핵심 요소가 됩니다. 예를 들어, 분자는 약물 효능으로, 화학 반응은 수율로 라벨링되며, 합성 절차는 수량과 시간이 섞인 자연어 텍스트로 표현됩니다.

언어와 숫자를 함께 모델링하기 위한 기존 연구들에서는 LM의 성능을 향상시키기 위해 검증기(Cobbe et al., 2021; Li et al., 2023), 연쇄적 사고(CoT) 추론(Zhong et al., 2024; Wei et al., 2022; Lee & Kim, 2023), 계산기나 코드 인터프리터(Qu et al., 2025; Gao et al., 2023)의 사용을 제안했습니다. 모델 수준에서는 숫자를 뒤집거나(Zhang-Li et al., 2024), 오른쪽에서 왼쪽으로 토큰화하거나(Singh & Strouse, 2024; Lee et al., 2023), 여러 숫자 토큰을 함께 예측하는(Bachmann & Nagarajan, 2024) 등의 맞춤형 아이디어들이 제안되었습니다. 그럼에도 불구하고, LM은 세 자리 곱셈과 같은 간단한 산술 작업에서도 어려움을 겪는 것으로 악명이 높습니다(Dziri et al., 2024).

저희는 과제를 재구성하거나, 계산기를 사용해 사후에 답을 수정하려 하거나, 훨씬 더 많은 컴퓨팅 자원을 사용하는(CoR) 것과 같은 이 모든 전략들이 '여러 가지 이유로 LM의 숫자 표현이 취약하다'는 근본적인 문제를 회피하고 있다고 주장합니다.

1. 토큰화 (Tokenization): 표준적인 서브워드(subword) 토큰화는 숫자를 임의의 토큰으로 분리하여 그 구조를 파괴하고 상당한 양의 수치적 정보를 잃게 만듭니다 (Wallace et al., 2019). 이를 완화하는 전략으로는 과학적 표기법(Zhang et al., 2020)이나, 각 자릿수의 10진 순서를 보존할 수도 있는 숫자 단위(digit-level) 토큰화(Geva et al., 2020; Born & Manica, 2023) 등이 있습니다.

2. 임베딩 (Embedding): 기본적으로 LM은 숫자 토큰 임베딩이 다른 토큰들과 똑같이 학습되기 때문에 데이터로부터 숫자의 구조를 다시 복원해야 합니다. 이를 완화하기 위해, 수리력(numeracy)을 보존하는 다양한 종류의 단어 임베딩이 존재하며(Sundararaman et al., 2020; Born & Manica, 2023; Golkar et al., 2023), 이는 종종 위치 인코딩(positional encodings)과 유사하고 때로는 모듈러 산술(modular arithmetics)을 위한 각도 임베딩(angular embeddings)과 같은 특수한 경우에 맞게 조정되기도 합니다 (Stevens et al., 2024; Saxena et al., 2024).

3. 순차적 예측 (Sequential prediction): 토큰 단위의 디코딩 방식은 숫자에서 높은 자릿수가 갖는 더 큰 중요성을 고려하지 못합니다. Zhang-Li et al. (2024)은 자릿수 순서를 뒤집고, 덧셈과 곱셈에 대해 인간에게서 영감을 받은 단계별 계산 방식을 사용하는 것이 정확도를 향상시킨다는 것을 발견했습니다.

4. 훈련 목표 (Training objective): 교차 엔트로피(CE) 손실은 명목 척도(nominal scale)를 가정하므로 숫자 간의 근접성을 전달하지 못하며, 이는 사실상 준지도적(semi-supervised) 환경을 만듭니다. 예를 들어, 정답이 2일 때 3을 예측하는 것이 9를 예측하는 것보다 일반적으로 더 낮은 손실을 유발하지 않습니다.

본 논문에서는 수학 문장제 문제나 과학 데이터셋과 같이 텍스트와 수치 데이터가 결합된 자료를 더 잘 다룰 수 있도록, 언어 모델(LM)에 더 나은 귀납적 편향(inductive biases)을 부여하고자 합니다. 저희는 수치적 근접성을 존중하며 표준적인 교차 엔트로피(CE)와 효과적으로 결합될 수 있는, 숫자 토큰에 대한 두 가지 버전의 회귀 손실(regression loss)을 제안합니다 (그림 1a). 숫자 토큰 손실(NTL)의 첫 번째 버전은 정답 레이블의 수치 값과, 예측된 클래스 확률에 각 숫자 토큰 값을 가중치로 부여한 값 사이의 평균 제곱 오차(MSE)를 계산합니다. 두 번째 버전은 예측된 숫자 확률 분포와, 정답 레이블의 원-핫 인코딩(one-hot encoding)인 실제 분포(ground truth distribution) 사이의 바서슈타인(Wasserstein) 거리를 계산합니다.

두 경우 모두, NTL은 다음과 같은 핵심적인 특징들을 가집니다.

(1) NTL은 모델에 구애받지 않습니다(model agnostic). 이는 트랜스포머, 맘바 등 어떠한 언어 모델이나 인코더-디코더, 디코더-전용 등 어떠한 스타일에도 적용될 수 있습니다.

(2) NTL은 어휘에 대해 최소한의 가정만을 하므로 모든 LM에 플러그 앤 플레이(plug-and-play) 방식으로 적용할 수 있습니다. 이는 토큰(문자열)과 해당 수치 값(실수) 사이의 매핑만 필요로 하므로, 숫자 단위(digit-level) 토큰화뿐만 아니라 여러 자릿수(multi-digit) 토큰화와도 호환됩니다¹.

(3) NTL은 계산 오버헤드를 추가하지 않습니다. 가장 성능이 좋은 NTL 버전(NTL-WAS)조차 교차 엔트로피에 비해 손실 계산 속도를 단 1% 늦출 뿐입니다. 이 차이는 전체 훈련 단계를 고려하면 무시할 수 있는 수준이 됩니다(나중에 그림 3 참조).

또한, 저희의 경험적 분석은 다음의 사실들을 보여줍니다:

(4) NTL은 단독으로 교차 엔트로피를 사용하는 것에 비해, 다양한 아키텍처에 걸쳐 수학 과제에서 일관되게 성능을 향상시킵니다.

(5) 실제 회귀 과제에서, NTL을 적용한 LM은 회귀 헤드(regression head)와 동등한 성능을 보였으며, 표준 CE를 사용한 LM에 비해서는 10% 더 높은 성능을 보였습니다.

(6) NTL은 텍스트로만 구성된 과제에서는 성능을 저해하지 않으며, (7) NTL은 수십억 파라미터 규모의 모델까지 잘 확장됩니다. 따라서 LLM 사전 훈련 중에 NTL을 사용하는 것을 반대할 이유가 없습니다.

---

2. Number Token Loss (NTL)

모든 언어 모델(LM)의 토큰 중 일부는 필연적으로 텍스트가 아닌 숫자(digit)나 수(number)에 해당합니다. 저희의 기본 아이디어는 이러한 숫자 토큰들의 로짓(logits)을 해당 토큰의 수치 값과 결합하여 손실을 계산하는 것입니다. 이러한 손실은 숫자 토큰들의 수치적 근접성을 고려함으로써 교차 엔트로피를 효과적으로 보강할 수 있습니다. 참고로, NLP 분야 밖에서는 '분류를 통한 회귀'에 대한 일부 체계적인 연구들이 존재하지만(Shah & Aamodt, 2023; Stewart et al., 2023), LLM에 원활한 통합을 가능하게 하는 원칙적인 접근법은 전무한 실정입니다.

$L_p$ 노름(norm) 기반 NTL (예: NTL-MSE)

이 손실 함수는 예측된 토큰 확률들을 실수 값 출력으로 매핑하는데, 이는 각 확률과 그에 해당하는 숫자 토큰 값의 내적(dot product)을 계산함으로써 이루어집니다 (그림 1a 참조). 이러한 변환을 통해, 예측된 출력을 실제 정답 토큰의 수치 값과 비교하기 위해 MSE와 같은 표준 회귀 손실을 적용할 수 있게 됩니다.

모델 $f(\cdot)$, 입력 토큰 $x_{\le i}$ ($i \le N$), 그리고 어휘집 $\mathcal{V}$가 있다고 가정합니다. 예측된 확률 분포를 $\hat{\mathbf{y}}_i := f(x_{\le i})$라고 하고, $y_i$는 실제 정답(ground truth) 토큰의 수치 값을 나타내는 원-핫(one-hot) 레이블입니다. 또한 $V: \mathcal{V} \rightarrow \mathbb{R}$는 토큰(문자열)을 해당 수치 값(실수)으로 변환하는 맵(map)이며, 인덱스 범위 $s...t$는 숫자 토큰들을 나타냅니다. 그러면 NTL-MSE는 다음과 같이 계산됩니다:

주목할 점은, CE와 같은 명목 척도 손실 대신 NTL-MSE는 숫자 간의 근접성을 효과적으로 전달한다는 것입니다. 예를 들어, 정답 레이블이 4일 때 LM이 9 대신 5를 예측하면 손실이 더 낮아지며, 이는 우리의 직관적인 기대와 일치합니다. 이는 수의 근접성과 관계없이 일정한 손실을 부여하는 명목적 특성을 가진 CE와는 대조적입니다 (그림 1b 참조).

NTL-MSE에서 p-차수(p-order)를 변경함으로써, NTL-MAE와 같은 다양한 $L_p$-노름 손실을 얻을 수 있습니다. 후버(Huber) 손실 또한 호환됩니다. NTL-$L_p$가 손실 함수의 한 계열을 설명하지만, NTL-MSE는 이미 Lukasik et al. (2025)의 동시 연구에서 RAFT라는 이름으로 제안되었으며, 최대 다섯 자리 숫자를 사용하는 순수 회귀 작업에서 LLM의 성능 향상을 보여주었습니다.

그러나 NTL-$L_p$는 유일하지 않은 최솟값(non-unique minimum)을 가지므로, 잘못된 예측에 대해 비정상적으로 낮은 손실을 반환할 수 있습니다. 예를 들어, 정답 레이블이 4인 샘플에 대해 모델이 0에 50%, 토큰 8에 50%의 확률을 할당했다고 가정해 봅시다. 이 경우 NTL은 0이 됩니다 (그림 2 참조). 소프트맥스가 로짓(logit) 차이를 강조하기 때문에 이러한 경우는 드물지만, NTL과 CE 손실을 결합하는 것이 이러한 비정상적인 경우를 바로잡는 데 도움이 됩니다. 하지만 이러한 유일하지 않은 최솟값 문제를 더 체계적으로 해결하기 위해, 저희는 두 번째로 개선된 버전을 제안합니다.

바서슈타인-1(Wasserstein-1) 거리를 이용한 NTL (NTL-WAS)

숫자 토큰의 예측 확률 분포와 실제 정답(ground truth) 분포 사이의 유사도를 측정하기 위해, 저희는 최적 수송(Optimal Transport, OT) 이론에서 영감을 얻어 이산(discrete) 바서슈타인-1 거리를 활용합니다. 이는 일반적으로 다음과 같이 정의됩니다:

여기서 $u_i$와 $v_j$는 점(point)을, $P$와 $Q$는 각각에 해당하는 확률을, 그리고 $c$는 수송 비용을 명시하는 함수를 나타냅니다. $\gamma$는 $P$와 $Q$ 사이의 결합(coupling)이며, $\gamma_{ij}$는 $u_i$에서 $v_j$로 수송되어야 할 질량(mass)을 명시합니다.

저희는 비용 함수 $c$를 숫자 토큰 값들 사이의 유클리드 거리로 정의하여, 예측 분포 $\hat{\mathbf{y}}_i$와 정답 분포 $\mathbf{y}_i$ 사이의 차이를 측정하기 위해 OT를 적용합니다:

비용 함수에 대한 참고: 식 (3)은 매우 유연합니다. 비용 함수 $c$를 변경함으로써, 숫자 토큰이 임의의 비유클리드(non-Euclidean) 공간에 존재할 때도 NTL을 적용할 수 있습니다. 비용 함수는 거리 메트릭(distance metric)의 정의를 따를 필요가 없으며, 대신 숫자 토큰들 간의 쌍별(pairwise) 행렬로 지정될 수 있습니다. 따라서 NTL은 모듈러 산술(modular arithmetics)과 같은 특이한 경우에도 유용할 수 있습니다 (Charton, 2023; Kera et al., 2024; Gromov, 2023). 본 논문에서는 일반적인 적용 가능성 때문에 주로 표준 유클리드 거리를 가정합니다. 비유클리드 비용이 유용한 실용적인 예시로는, 종종 매우 큰 수에 대한 개별 토큰을 포함하는 여러 자릿수(multi-digit) 토큰화기가 있습니다 (비유클리드 비용에 대한 명시적인 결과는 섹션 4.5에 포함되어 있습니다).

식 (3)의 값을 계산하는 것은 선형 계획법(linear program)을 풀어야 하므로 일반적으로 미분 가능하지 않습니다. 일반적인 경우에는 엔트로피 정규화(entropic regularization)를 통해 근사치를 구할 수 있지만(Cuturi, 2013), 저희가 $W_c$를 적용하는 방식에는 효율적이고 미분 가능한 계산을 가능하게 하는 두 가지 특별한 경우가 있습니다.

첫째, 만약 $\mathbf{y}_i$가 원-핫(one-hot) 벡터라면, $\mathcal{L}_{\text{NTL-WAS}}$는 정답 레이블의 수치 값과 다른 숫자 토큰 값들 간의 절대 차이의 가중 합과 일치합니다:

둘째, 만약 숫자 토큰 인덱스 $s...t$가 수치 값 $\mathbf{V}^{s:t}$에 따라 정렬되어 있고 그 값들이 등간격(equidistantly spaced)이라면, 바서슈타인-1 거리는 누적 분포 함수(CDF)를 사용하여 계산할 수 있습니다:

$\mathcal{L}_{\text{NTL-WAS-CDF}}$의 장점은 레이블 $\mathbf{y}_i$가 원-핫일 필요가 없다는 것입니다. 대신, 예를 들어 숫자 토큰에 대한 레이블 스무딩(label smoothing)을 통해 얻어진 임의의 목표 분포를 지원합니다 (Wang et al., 2025).

실제로는, 달리 언급되지 않는 한, 저희는 식 (4)를 통해 $\mathcal{L}_{\text{NTL-WAS}}$를 계산합니다. 이는 식 (5)보다 230배 더 빠르고, 정렬이나 등간격 배치를 요구하지 않아 숫자 단위(digit-level) 토큰화를 넘어서도 적용할 수 있기 때문입니다. 그림 1b에서 볼 수 있듯이, $\mathcal{L}_{\text{NTL-WAS}}$는 숫자 간의 근접성을 올바르게 전달할 뿐만 아니라, $\mathcal{L}_{\text{NTL-MSE}}$에서 발생하는 유일하지 않은 최솟값(non-unique minima) 문제도 제거합니다 (그림 2). NTL의 두 버전 모두 $\lambda$(기본값 0.3)로 스케일링되어 표준 CE 손실에 더해집니다:

참고로, NTL의 두 버전 모두 모든 비(非)숫자 토큰에 대해서는 0의 손실을 산출합니다

---

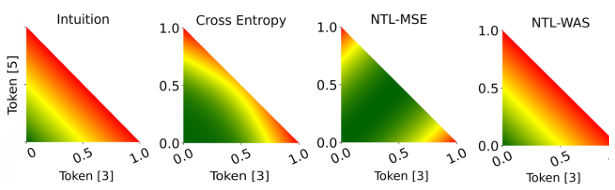
그림 2. 이 히트맵은 실제 정답(ground truth)이 토큰 4일 때, 토큰 3과 5에 대한 클래스 확률의 조합에 따른 각각의 손실 값을 보여줍니다. NTL-WAS의 동작 방식은 손실 함수로서 기대되는 직관적인 형태에 가장 가까운 반면, NTL-MSE는 유일한 최솟값(unique minimum)을 갖지 않습니다.

---

3. Experiment Setup

3.1. Backbone T5 and Model Variants

달리 명시되지 않는 한, 저희는 대부분의 실험에서 T5 백본(Raffel et al., 2020)(부록 A.3)을 사용합니다. 이는 유연한 인코더-디코더 아키텍처와 다양한 자연어 처리 과제에서의 성공 때문입니다. 저희는 transformers(Wolf et al., 2020)의 T5 구현체와 언어 모델링 트레이너를 기반으로 구축했습니다. 섹션 4.1의 다중 과제 수학 실험에서는 2억 2천만(220M) 개의 파라미터를 가진 T5-Base를, 섹션 4.7의 확장성 실험에서는 T5-3B를 사용합니다. 절제 연구(ablation studies) 및 기타 실험에는 6천만(60M) 개의 파라미터를 가진 T5-Small을 사용합니다. NTL의 모델에 구애받지 않는(model-agnostic) 특성을 보여주기 위해, 저희는 GPT-2와 IBM Granite 모델 변형에서도 이를 평가합니다. 모델은 항상 사전 훈련된 가중치로 초기화합니다.

이전 연구(Geva et al., 2020)를 바탕으로, 저희는 모든 숫자를 숫자 단위(digit level)로 토큰화하고 다른 모든 토큰은 변경하지 않는 방식으로 토큰화 기법을 조정했습니다. 비록 NTL의 두 버전 모두 모든 토큰화기와 호환되지만, 저희 실험에서는 한 자리 숫자(single-digit) 토큰화가 수학 과제에서 CE와 NTL 모두의 성능을 향상시켰습니다 (하위 섹션 4.5 참조).

3.2. Baselines

저희는 세 가지 관련 방법과 비교합니다.

첫 번째로, Regression Transformer(Born & Manica, 2023)는 각 숫자의 위치와 값을 모두 고려하여 숫자를 숫자 단위(digit level)로 토큰화하고, 숫자의 상대적 근접성을 보존하는 고정된 숫자 임베딩을 활용합니다 (자세한 내용은 부록 A.4 참조).

두 번째로, xVal(Golkar et al., 2023)은 실수를 단일 [NUM] 토큰에 해당 수치 값을 곱하여 인코딩하는 방식입니다. 디코딩 시에는 숫자/회귀 헤드가 값을 예측하고 토큰 헤드는 시퀀스를 출력하며, 추론 과정에서 [NUM]을 대체합니다. 그러나 이 방식은 T5와 호환되지 않으며(부록 A.5 참조) 빔 탐색(beam search) 디코딩에 문제가 있습니다. 따라서 저희는 실험에서 xVal 인코더와 마스크 언어 모델링(masked language modeling)을 사용합니다.

셋째, 가우시안 교차 엔트로피(Gaussian Cross Entropy)(또는 가우시안 레이블 스무딩; Wang et al. (2025))는 연속적인 값을 갖는 토큰에 대한 표준 CE의 한계를 해결합니다. 원-핫 인코딩된 레이블 대신, 가우시안 분포를 실제 숫자 레이블에 중심을 둡니다. 이 방식에서는, 주변의 숫자 토큰들이 부분적인 확률 질량(probability mass)을 받아 수치 값의 연속적인 특성을 반영합니다. 숫자 레이블 $y_i$가 주어지면, 그것의 원-핫 벡터 $\mathbf{y}_i$는 다음과 같은 가우시안 분포로 대체됩니다:

여기서 $\sigma$는 스무딩의 폭을 결정합니다. 목적 함수는 여전히 교차 엔트로피이지만, 이제는 수정된 레이블 $\tilde{\mathbf{y}}_i$와 예측 분포 $\hat{\mathbf{y}}_i$ 사이에서 계산됩니다:

명백한 단점은 이 스무딩이 완전히 인위적이라는 점입니다. 즉, 레이블에는 실제 불확실성이 없습니다. 이것이 기술적으로는 부정확한 레이블을 제공하지만, 주변 숫자 토큰들 간의 내재된 유사성을 포착하고 숫자 공간에서의 연속성을 보존하는 것을 보장합니다. Wang et al. (2025)은 이 방법이 순전히 범주형인 토큰에 대한 분류 성능을 변화시키지 않는다는 것을 발견했습니다.

---

4. Experimental Results

4. 실험 결과

모든 실험에 걸쳐, 저희는 항상 NTL을 CE와 함께 최적화합니다 (식 6 참조; 기본 $\lambda = 0.3$). 간결함을 위해, 저희는 이를 그냥 NTL-MSE 또는 NTL-WAS라고 지칭하겠습니다.

4.1. NTL Improves Performance in Arithmetics

모델의 수학적 능력을 시험하기 위해, 저희는 DeepMind의 수학 Q&A 데이터셋(Saxton et al., 2019)에서 2,500만 개 이상의 샘플을 사용합니다. 이 데이터셋은 두 가지 종류의 테스트를 포함합니다: 훈련 세트에 등장하는 각 질문 유형에 대한 보간(interpolation) 테스트와, 훈련 시 보았던 것 이상의 다양한 난이도 축에 따른 일반화 성능을 측정하는 외삽(extrapolation) 테스트입니다. 데이터셋에 대한 더 자세한 정보는 부록 A.6.1에 제공됩니다.

4.1.1. MULTITASK MATHEMATICS DATASET

저희는 이 데이터셋의 두 테스트 세트에서 모든 모델을 평가했으며, 정확도(정확하게 예측된 숫자의 비율)뿐만 아니라 평균 절대 오차(MAE)와 R² 점수를 보고합니다. 데이터셋에 매우 큰 값들이 포함되어 분포가 치우쳐 있으므로, MAE와 R² 점수를 계산하기 전에 예측값과 실제 정답(ground truth) 숫자에 log10 변환을 수행합니다. 모든 모델은 배치 크기 32로 약 100만(1M) 스텝 동안 훈련되었습니다. 모델의 훈련 하이퍼파라미터에 대한 더 자세한 내용은 부록 A.6에서 찾을 수 있습니다.

표 1. 수학 데이터셋에 대한 평가

표 1. (a) 보간(Interpolated) 테스트 데이터

모델	손실 함수	정확도	MAE	R²
T5	CE	0.64	0.13	0.97
T5	NTL-MSE	0.72	0.11	0.97
T5	NTL-WAS	0.75	0.10	0.98
T5	NTL-MAE	0.74	0.10	0.97
RT	CE	0.71	0.11	0.97
xVal	MSE	0.10	0.26	0.97

표 1. (b) 외삽(Extrapolated) 테스트 데이터

모델	손실 함수	정확도	MAE	R²
T5	CE	0.367	0.785	0.913
T5	NTL-MSE	0.428	0.779	0.909
T5	NTL-WAS	0.432	0.744	0.913
T5	NTL-MAE	0.427	0.792	0.906
RT	CE	0.404	0.987	0.738
xVal	MSE	0.058	0.826	0.819

표 1과 그림 A1의 결과는 기본 T5 모델이 두 가지 NTL 변형으로부터 명확한 이점을 얻는다는 것을 보여줍니다. 실제로, 보간(interpolation) 작업에서 NTL-WAS는 기본 T5에 비해 정확도가 10% 이상 증가했습니다. NTL-WAS는 세 가지 모든 평가지표와 보간 및 외삽(extrapolation) 작업 모두에서 최고의 성능을 보이는 것으로 나타났습니다. 더욱이, NTL은 RT나 xVal과 같은 경쟁 방법들보다 일관되게 우수한 성능을 보였습니다. 이는 언어 모델(LM)에서의 숫자 표현이 아키텍처에 구애받지 않는 사소한 손실 함수 수정을 통해 효과적으로 개선될 수 있다는 저희의 가설을 확인시켜 줍니다.

xVal은 회귀 헤드(regression head)를 갖추고 있기 때문에 숫자가 정확하게 예측되지 않습니다. 따라서 xVal의 정확도 값은 예측값을 소수점 둘째 자리에서 반올림한 것을 의미합니다. xVal의 저조한 성능은 사용된 데이터셋의 광범위한 숫자 범위 때문일 가능성이 높습니다. xVal의 유효 숫자 범위는 숫자 토큰 임베딩의 스케일링 방식과 백본의 사전 계층 정규화(pre-layer-norm)의 조합으로 인해 [−5, 5]로 제한됩니다 (Xiong et al., 2020; Golkar et al., 2023). 이를 고려하여 저희는 xVal을 위한 데이터셋을 log(1+x)로 스케일링했습니다. 하지만 이는 큰 숫자들의 임베딩이 매우 유사해져 모델이 더 이상 이들을 적절히 구분할 수 없게 됨을 의미합니다. xVal의 처리 방식에 어떠한 수정도 가하지 않은 직접적인 비교를 위해, 저희는 Golkar et al. (2023)의 세 자리 곱셈 실험을 반복했습니다. 이 실험에서도 저희의 방법이 xVal을 능가했으며, 자세한 내용은 부록 A.5에서 확인할 수 있습니다.

4.1.2. Ablation Studies

손실 함수의 변형이 미치는 영향을 조사하기 위해, 저희는 9가지의 서로 다른 구성을 테스트하는 광범위한 실험을 수행했습니다. 구성은 표준 교차 엔트로피 손실, NTL-MSE와 NTL-WAS(각각 λ ∈ {0.3, 0.8, 2}인 경우), NTL-MAE, 그리고 NTL-Huber입니다. 이 모델들의 훈련은 원본 데이터셋의 하위 과제(10만 개 샘플)에서 수행되었으며, 이 과제는 산술 표현식을 포함하는 짧은 자연어 질문을 입력으로 받고 단일 정수를 출력하는 기본적인 정수 산술 Q&A 쌍으로 구성됩니다. 보간 및 외삽 테스트 세트에서의 성능 비교는 표 2에 나와 있습니다.

표 2. NTL 손실 함수 변형 평가

표 2. (a) 보간(Interpolated) 테스트 데이터

손실 함수	λ	정확도	MAE	R²
CE		0.34±0.01	2.15±0.08	0.95±0.01
NTL-MSE	0.15	0.44±0.02	0.92±0.05	0.99±0.00
	0.3	0.41±0.01	1.02±0.06	0.99±0.00
	0.8	0.37±0.02	1.29±0.11	0.99±0.00
	2.0	0.33±0.01	1.67±0.20	0.97±0.01
NTL-WAS	0.15	0.44±0.02	0.93±0.01	0.99±0.00
	0.3	0.43±0.05	0.91±0.06	0.99±0.00
	0.8	0.43±0.04	0.94±0.07	0.99±0.00
	2.0	0.41±0.06	1.01±0.08	0.99±0.00
NTL-Huber	0.3	0.44±0.02	0.89±0.03	1.00±0.00
NTL-MAE	0.3	0.45±0.02	0.89±0.07	0.99±0.00

표 2. (b) 외삽(Extrapolated) 테스트 데이터

손실 함수	λ	정확도	MAE	R²
CE		0.05±0.00	61.91±1.31	0.61±0.01
NTL-MSE	0.15	0.09±0.01	57.13±1.51	0.68±0.01
	0.3	0.09±0.01	60.99±1.35	0.65±0.01
	0.8	0.08±0.01	58.35±1.06	0.68±0.01
	2.0	0.07±0.01	59.48±2.72	0.66±0.02
NTL-WAS	0.15	0.09±0.00	57.31±0.57	0.68±0.00
	0.3	0.10±0.01	58.18±1.89	0.68±0.02
	0.8	0.10±0.02	59.46±1.38	0.66±0.01
	2.0	0.10±0.01	62.29±1.04	0.64±0.01
NTL-Huber	0.3	0.10±0.01	58.81±1.67	0.67±0.01
NTL-MAE	0.3	0.10±0.01	57.99±1.48	0.67±0.01

우선, 모든 종류의 NTL이 표준 교차 엔트로피(CE) 손실보다 일관되게 우수하다는 것이 명백합니다. 평균과 표준편차는 4번의 서로 다른 훈련 실행을 통해 계산되었으며, 자세한 내용과 추가적인 평가지표는 부록 A.6.2에서 확인할 수 있습니다.

표 2의 절제 연구(ablation studies)는 두 가지 NTL 변형 모두 CE 손실만 단독으로 사용하는 것에 비해 산술 성능을 향상시킨다는 저희의 발견을 뒷받침합니다. 추가적으로, NTL-WAS는 보간(interpolation) 및 외삽(extrapolation) 테스트 세트 모두에서 대부분 NTL-MSE보다 우수한 성능을 보입니다. 테스트된 NTL의 가중치 중에서는 $\lambda=0.3$이 두 손실 변형 모두에서 최고의 성능을 보였습니다. 흥미롭게도, 저희는 NTL-Huber가 NTL-WAS와 대등한 결과를 보이고, NTL-MAE는 때때로 더 우수한 결과를 달성한다는 것을 발견했습니다.

모든 실험에 걸쳐 R²는 높은 값을 달성했는데, 이는 정확도와는 대조적으로 보입니다. 오차 분포를 면밀히 조사한 결과, 이는 많은 예측이 엄밀하게는 정확하지 않더라도 수치적으로는 실제 정답(ground truth)에 매우 가깝기 때문인 것으로 밝혀졌습니다. 이러한 작은 오차들은 R²에는 매우 제한적인 영향을 미치지만, 정확도에는 여전히 영향을 줍니다.

4.1.3. GAUSSIAN CROSS ENTROPY

표 3. 가우시안 교차 엔트로피 (GCE)
GCE와 NTL의 단독 및 조합 효과. 4번의 실행에 대한 평균과 표준편차.

GCE	NTL	정확도	MAE	R2
보간 (Interpolation)
✗	✗	0.34	2.15	0.95
✗	✓	0.43	0.91	0.99
✓	✗	0.42	0.95	0.99
✓	✓	0.48	0.76	0.99
외삽 (Extrapolation)
✗	✗	0.05	61.92	0.61
✗	✓	0.10	58.18	0.68
✓	✗	0.10	58.55	0.65
✓	✓	0.10	66.67	0.59

Wang et al. (2025)이 제안한 가우시안 교차 엔트로피(GCE)는 숫자 토큰 간의 근접성을 전달하기 위한 대안적이면서도 상호 보완적인 수단입니다. 저희는 이 방법이 본질적으로 레이블을 흐리게 만들고 기술적으로는 부정확한 토큰에 확률 질량을 할당하기 때문에 덜 원칙적이라고 주장합니다. 그럼에도 불구하고, 저희는 기본 CE 목적 함수를 GCE 목적 함수로 대체하여 그 성능을 평가했으며, $\sigma = 0.5$일 때 가장 좋은 결과를 얻는다는 것을 발견했습니다 (표 A6).

보간 및 외삽 세트에 대한 실험들은 NTL과 GCE 모두 모델 성능을 향상시키지만, NTL이 더 큰 개선을 이끌어내므로 일반적으로 더 선호된다는 것을 시사합니다. 더 나아가, 저희는 NTL과 GCE를 함께 사용했을 때의 성능을 조사했습니다. 이 설정에서는 레이블이 더 이상 원-핫 인코딩이 아니므로, 임의의 목표 분포로 훈련할 수 있는 NTL-WAS-CDF 공식(식 5)을 사용했습니다. 보간 세트에서는 NTL과 GCE의 조합이 가장 좋은 결과를 냈습니다. 이러한 실험들은 NTL과 GCE가 특정 과제에 대해서는 상호 이익이 될 수 있음을 시사합니다.

4.2. Training with NTL Is Efficient

그림 3. 실행 시간 비교. 평균 숫자 토큰 비율 80% 조건에서, 네 가지 손실 함수를 단독 실행(위)과 전체 훈련 단계(아래)의 두 가지 구성으로 벤치마킹하여 계산 오버헤드를 보여줍니다.

잠재적인 계산 오버헤드를 평가하기 위해, 저희는 네 가지의 서로 다른 손실 구성에 걸쳐 포괄적인 벤치마킹을 수행했습니다. 구성은 기준선 역할을 하는 CE 손실, CE와 NTL-MSE, 식 (5)에 따라 구현된 CE와 NTL-Wasserstein(NTL-WAS-CDF), 그리고 최적화된 버전인 CE와 NTL-WAS(식 4)입니다. 저희는 손실 계산 자체의 독립적인 계산 오버헤드와, 순전파(forward pass), 역전파(backpropagation), 옵티마이저 단계를 포함하는 전체 훈련 단계 내에서의 영향을 정량화하기 위해 두 가지 다른 시나리오에서 이 손실 함수들을 평가했습니다. 저희는 순전파와 훈련 단계 모두에서 입력의 토큰 수를 표준화했으며, 모든 실험에 걸쳐 숫자 토큰의 위치는 무작위로 설정했지만 그 비율은 일관되게 유지했습니다. 각 손실 함수는 GPU에서 100번의 반복을 통해 평가되었습니다. 그림 3의 결과는 NTL-MSE와 NTL-WAS가 두 벤치마크 시나리오 모두에서 미미한 계산 오버헤드만을 유발한다는 것을 보여줍니다. 이는 각 벤치마크가 CE 손실의 런타임과 각각의 NTL 변형의 런타임을 합한 값을 포함하기 때문입니다.

주목할 점은, NTL-WAS만 단독으로 계산하는 것이 CE만 단독으로 계산하는 것보다 약 125배 빠르다는 것입니다. 이는 어휘집의 아주 작은 일부 토큰만이 숫자 토큰이기 때문에 가능한 일입니다. 손실 계산 시간만 평가할 때, CE 손실에 NTL을 추가하는 것은 1%(NTL-WAS)에서 2.9%(NTL-MSE)에 이르는 계산 오버헤드를 유발하며, 덜 효율적인 NTL-WAS-CDF의 경우에는 무려 286%까지 증가합니다. 그러나 전체 훈련 단계 동안에는 순전파, 역전파, 옵티마이저 단계로 구성된 전체 계산량이 지배적이 되므로 상대적인 오버헤드는 무시할 수 있는 수준이 됩니다. 예를 들어, CE 대비 NTL-WAS-CDF의 상대적 오버헤드는 4.4%로 감소합니다.

4.3. NTL Can Match Regression Models

표 4. 회귀 과제에서의 NTL 성능
NTL은 회귀 헤드 모델과 대등한 성능을 보입니다. 5번의 실행에 대한 평균과 표준편차. BERT, RoBERTA, XLNet 값은 Weller & Seppi (2020)에서 가져왔습니다.

모델	손실 함수	회귀 헤드	RMSE	Pearson
T5	CE	✗	2.01±0.01	0.41±0.00
T5	NTL-WAS	✗	1.81±0.01	0.44±0.00
T5	MSE	✓	1.82±0.01	0.45±0.00
BERT	MSE	✓	1.62	0.47
RoBERTA	MSE	✓	1.61	0.47
XLNet	MSE	✓	1.74	0.46

이상적으로, 언어 모델(LM)은 분자의 속성을 추정하는 것과 같이 오직 수치 값 예측에만 초점을 맞춘 과제도 해결할 수 있어야 합니다. 이러한 과제는 종종 평균 제곱 오차(MSE)와 같은 적절한 손실 함수를 사용할 수 있게 해주는 LM의 회귀 헤드(regression head)를 통해 접근합니다. NTL이 순전히 토큰 기반으로 회귀 과제를 해결하는 능력을 시험하기 위해, 저희는 농담의 유머 수준을 예측하는 과제인 rJokes 데이터셋(Weller & Seppi, 2020)으로 모델을 훈련했습니다. 훈련-테스트 분할은 데이터셋과 함께 제공됩니다.

표 4에서는 CE, NTL-WAS를 적용한 T5 모델과 회귀 헤드를 결합한 T5 모델의 결과, 그리고 rJokes 벤치마크(Weller & Seppi, 2020)의 결과를 보여줍니다. 저희는 신뢰할 수 있는 지표를 확보하기 위해 세 번의 독립적인 실행에 걸쳐 T5 모델의 모든 버전을 평가했습니다.

결과적으로 NTL은 표준 CE보다 성능을 월등히 향상시켰으며 회귀 헤드 모델과 대등한 성능을 보였습니다. 이는 전용 회귀 헤드에 의존하는 모델들과 달리, NTL이 토큰 수준에서 작동하면서도 비(非)수치적 과제에도 여전히 활용될 수 있다는 점을 고려할 때 주목할 만한 결과입니다. 비록 회귀 헤드를 가진 BERT, RoBERTa, XLNet이 NTL-WAS로 훈련된 T5보다 성능이 더 좋지만, 파라미터 수의 차이를 고려하면 그 성능 격차는 크지 않습니다. 저희는 이것이 해당 모델들이 저희의 T5-small 모델보다 거의 두 배 많은 파라미터를 가지고 있기 때문이라고 생각합니다. 자세한 내용과 추가적인 평가지표는 부록 A.6.3에서 확인할 수 있습니다.

4.4. NTL Is Model-Agnostic

손실 함수로서, NTL은 Mamba와 같이 트랜스포머를 넘어서는 언어 모델(LM)을 포함한 임의의 모델을 훈련시키는 데 적용될 수 있습니다. 지금까지 설명된 실험들은 인코더-디코더 트랜스포머 아키텍처에 기반한 T5 모델로 수행되었습니다. 이 섹션에서는 디코더-전용 모델인 GPT-2(Radford et al., 2019)와 IBM Granite(IBM Research, 2024)을 NTL로 훈련시키는 것의 효과를 입증합니다. 저희는 1억 2,500만(125M)에서 20억(2B) 파라미터에 이르는 모델 크기를 테스트합니다.

이를 위해, 저희는 길이 일반화 과제(length generalization task)와 매우 유사한 산술 곱셈 과제를 구성했습니다(Jelassi et al., 2023). 이 과제는 $k$자리와 $l$자리의 두 숫자를 곱하는 것으로 구성되며, 훈련 시에는 $k, l \in [1,..,5]$이고 테스트 시에는 $k, l \in [1,..,6]$입니다. 저희는 최대 5×5자리 숫자를 곱하는 것을 포함하는 처음 보는 보간(interpolation) 샘플과, 적어도 하나의 여섯 자리 인수를 포함하는 곱셈인 외삽(extrapolation) 샘플에 대해 평균 절대 백분율 오차(MAPE)를 각각 보고합니다. 표 5에 제시된 결과는 디코더-전용 모델을 NTL로 훈련시키는 것의 효과를 보여주며, 이는 MAPE 측면에서 곱셈 과제의 성능을 일관되게 향상시킵니다.

표 5. 디코더-전용 모델에서의 NTL 성능
곱셈 과제에 대해 CE와 NTL로 GPT-2와 IBM Granite 변형 모델을 훈련했을 때의 MAPE. 모든 값은 오차 백분율입니다.

모델	크기	보간 (CE)	보간 (NTL)	외삽 (CE)	외삽 (NTL)
GPT2 Small	125M	0.55	0.49	1.11	1.00
GPT2 Medium	350M	0.43	0.42	0.82	0.82
GPT2 Large	774M	0.39	0.37	0.76	0.75
GPT2 XL	1.5B	0.43	0.40	0.83	0.82
Granite 3.2	2B	0.35	0.21	0.60	0.42
Granite 3.1 MOE	1B	0.28	0.15	0.68	0.23

NTL의 긍정적인 영향은 모든 모델 규모에 걸쳐 명백합니다. 주목할 점은, NTL로 인한 개선이 보간보다 외삽 환경에서 더 두드러진다는 것인데, 이는 NTL을 사용한 훈련이 훈련 분포를 넘어 일반화하는 모델의 능력을 향상시킨다는 것을 나타냅니다. 이는 수학적 과제에서의 저조한 외삽 능력 때문에 특히 의미가 있습니다(Razeghi et al., 2022). Granite 3.1과 같은 일부 모델은 NTL을 사용한 훈련으로부터 특히 이점을 얻으며, 평가된 모델들 중에서 가장 큰 성능 향상을 보였습니다(전체 평가는 부록 그림 A2 참조).

그림 4. 샘플 효율성. 곱셈 과제(GPT2 Small)에서 MAPE가 0.5 미만에 도달하기까지 필요한 에포크 수. NTL은 특히 더 긴 인수를 가진 샘플에 대한 샘플 효율성을 향상시킵니다.

더 나아가, 저희는 CE만 사용하는 것과 비교하여 곱셈 과제에서 NTL을 사용한 훈련의 샘플 효율성(sample efficiency)을 분석했습니다. 그림 4에서 드러나듯이, NTL로 훈련된 GPT2-Small은 0.5 미만의 MAPE를 달성하는 데 훨씬 적은 에포크(epoch)를 필요로 합니다. 이 효과는 더 큰 인수로 구성된 어려운 샘플에서 더 두드러집니다.

유사하게, 저희는 NTL을 사용할 때 평균 숫자 출력 분포가 정답 토큰에 더 날카롭게 집중되는 것을 관찰합니다(부록 그림 A4 참조).

4.5. NTL Is Effective for Different Tokenizations

T5 모델을 위한 저희의 표준 NTL-WAS 구현은, SentencePiece에 기반하며 여러 자릿수(multiple-digits)로 구성된 일부 토큰을 포함하는 표준 T5 토큰화기로부터 파생된, 맞춤형 한 자리 숫자(single-digit) 토큰화기를 사용합니다. 저희는 맞춤형 토큰화기와 손실 함수의 효과를 분리하여 분석하기 위해 추가적인 절제 연구(ablation studies)를 수행했습니다. 이를 위해, 저희는 rJokes 및 수학 Q&A 데이터셋에 대한 추가 실험을 진행했으며, 이 실험에서는 NTL-WAS 없이 한 자리 숫자 토큰화기를 사용하는 경우와, 여러 자릿수 토큰을 지원하는 더 일반적인 버전의 NTL-WAS를 사용하는 경우의 효과도 평가했습니다. 표 6의 rJokes 데이터셋 결과는 두 토큰화 방식 모두에서 NTL-WAS 손실의 효과성을 확인시켜주며, 한 자리 숫자 토큰화와 NTL-WAS의 조합이 가장 좋은 성능을 보입니다.

표 6. rJokes 데이터셋에서의 토큰화기 비교

모든 실험에 T5-small 사용. 4번의 실행에 대한 평균과 표준편차.

손실 함수	맞춤형 토큰화기	RMSE	Pearson
CE	✗	2.01±0.01	0.41±0.00
NTL-WAS	✗	1.97±0.01	0.41±0.00
CE	✓	2.02±0.01	0.41±0.00
NTL-WAS	✓	1.81±0.01	0.44±0.00
MSE	✗	1.82±0.01	0.45±0.00

표 7의 수학 Q&A 과제의 외삽(extrapolation) 테스트 세트에서도 유사한 경향이 관찰되며, 여기서 NTL-WAS는 두 토큰화 전략 모두에서 정확도를 향상시킵니다. 표 A5의 보간(interpolation) 테스트 세트에서는, NTL-WAS가 표준 토큰화기의 성능을 향상시키는 반면, 한 자리 숫자 토큰화기는 NTL-WAS 없이 사용했을 때 약간 더 나은 성능을 보였습니다. 외삽 과제와 rJokes 과제가 현실 세계의 시나리오를 더 가깝게 모방하기 때문에, 저희는 이러한 실험들이 특히 한 자리 숫자 토큰화와 결합될 때 NTL의 전반적인 이점을 더욱 강화한다고 주장합니다.

표 7. 다른 모델과 토큰화기에 대한 외삽 성능

손실 함수	맞춤형 토큰화기	정확도 (외삽)	Pearson (외삽)
CE	✗	0.05±0.00	0.81±0.01
NTL-WAS	✗	0.06±0.00	0.76±0.01
CE	✓	0.09±0.01	0.87±0.01
NTL-WAS	✓	0.10±0.01	0.88±0.01

더 나아가, 저희는 숫자를 여러 자릿수로 토큰화하는 모델에서 실용적인 문제를 관찰했습니다: 일부 토큰은 큰 수치 값을 가지며, 이는 특히 숫자 토큰이 불규칙하게 분포되어 있을 때 손실에 불균형적으로 영향을 미칩니다. 숫자 단위(digit-level) 토큰화와 유클리드 거리를 사용하는 NTL(지금까지 사용된 방식)에서는, 가장 멀리 떨어진 오답 숫자 토큰에 대한 손실이 가장 가까운 오답 숫자 토큰 손실의 9배를 초과할 수 없습니다². 하지만 어휘집에 1001과 같이 큰 숫자 토큰 하나가 있으면 이 비율을 1000배까지 왜곡시킬 수 있으며 심지어 훈련을 불안정하게 만들 수도 있습니다. NTL은 숫자 사이의 유클리드 거리를 사용하는 데 국한되지 않기 때문에(식 2 참조) 이러한 극단적인 경우를 본질적으로 완화할 수 있습니다. 이는 토큰 간의 거리를 압축(squash)하는 선택적인 재조정 계수(rescaling factor)를 통해 달성될 수 있습니다. 참고로, 숫자 단위 토큰화에서는 암묵적인 압축 계수가 9인 반면, 이를 1로 설정하면 사실상 표준 교차 엔트로피로 돌아갑니다. 따라서 압축은 기본 NTL과 CE 사이를 부드럽게 보간(interpolate)하는 것을 가능하게 합니다. 정수 곱셈 데이터셋(Jelassi et al., 2023)에서, 저희는 압축 계수 3을 사용한 GPT2-Large가 CE보다는 개선되었지만 MAPE로 측정했을 때 NTL보다는 성능이 저조하다는 것을 발견했습니다(표 A7).

전반적으로, 저희는 NTL이 안정적으로 작동하도록 숫자 단위 토큰화를 강제하는 것을 권장합니다.

4.6. NTL Does Not Hamper Text Learning

NTL을 사용한 훈련이 일반적인 텍스트 생성 과제에 단점을 야기하지 않는다는 것을 보장하기 위해, 저희는 독해력을 테스트하는 질의응답 데이터셋인 MultiRC 데이터셋(Khashabi et al., 2018)에 대한 실험을 수행합니다. 저희는 이 데이터셋을 다지선다형 과제로 평가하는 대신, 질문을 기반으로 모델이 답변을 생성하도록 훈련시키기 위해 데이터셋의 형식을 변경했습니다. 이를 위해, 저희는 지문과 그에 해당하는 질문을 추출하여 이어 붙여 입력을 구성하는 방식으로 데이터셋을 전처리합니다. 답변 필드는 모든 정답을 구분 기호로 이어 붙여 구성됩니다.

NTL은 답변에 포함된 숫자 토큰에만 적용되었으며, 이는 전체 답변 토큰의 1.5%에 불과합니다. 저희는 이 비율이 실제 텍스트 데이터셋을 거의 대표한다고 생각합니다. 표 8에는 검증 세트에서 3번의 실행에 걸쳐 평가된 평균과 표준편차가 나와 있습니다. 토큰 정확도뿐만 아니라 BLEU 및 ROUGE-1 점수도 NTL 추가에 영향을 받지 않았으며, CE만 사용했을 때와 동일한 수준을 유지했습니다.

이러한 결과는 NTL을 사용한 훈련이, 수치 데이터에 대한 이점이 제한적이거나 없는 과제에서 텍스트 이해 성능을 저해하지 않는다는 것을 보여줍니다. 이러한 발견은 NTL이 일반적인 텍스트 이해 및 생성 능력을 손상시키지 않으면서 언어 모델(LM) 훈련의 표준적인 개선 사항으로 통합될 수 있음을 강조합니다.

표 8. 표준 언어 모델링 과제에서의 NTL
NTL은 순수 텍스트 과제의 성능에 영향을 미치지 않습니다.

손실 함수	토큰 정확도	BLEU	ROUGE-1
CE	0.36±0.00	0.13±0.00	0.32±0.00
NTL-WAS	0.36±0.00	0.13±0.00	0.32±0.00

4.7. NTL Scales Well to LLM-Size

NTL을 대규모 언어 모델(LLM)에 통합할 수 있는 잠재력을 입증하기 위해, 저희는 30억(3B) 파라미터 버전의 T5 모델을 초등학교 수학 문제에 기반한 수학적 추론 벤치마크인 GSM8k 데이터셋(Cobbe et al., 2021)으로 훈련시킵니다. 이 데이터셋은 표준 LLM에게 상당한 도전 과제입니다. 예를 들어, 60억(6B) 파라미터 모델들은 초기에 미세 조정(fine-tuning) 후 22%의 정확도밖에 달성하지 못했습니다 (Cobbe et al., 2021).

저희 실험에서, GSM8K 데이터셋에 대해 CE 손실로 훈련된 T5-3B 모델은 13.5%의 top-1 정확도를 달성했습니다 (표 9 참조). NTL 손실을 사용한 훈련은 정확도를 17.7%까지 향상시키며, 이는 Gemma-2B(Team et al., 2024)와 같이 수학적 추론에 더 적합한 LLM의 성능과 필적하고, LLaMA-2 7B(14.6%)와 같은 더 큰 모델을 능가하는 수치입니다. GSM8K 과제와 예측된 해결책에 대한 정성적인 예시는 부록 예시 1에 제공됩니다.

표 9. GSM8k에서의 T5-3B 결과

손실 함수	정확도	Pearson
CE	13.5%	0.67
NTL-WAS	17.7%	0.72

주목할 점은, 특화된 훈련 접근법이 성능을 크게 향상시킬 수 있다는 것입니다. 예를 들어, 맞춤형 미세 조정 전략은 13억(1.3B) 파라미터 모델조차 81.5%의 정확도에 도달하게 했습니다 (Liu et al., 2023). 향후 연구에서는 NTL이 이러한 특화된 모델들을 어떻게 더욱 향상시킬 수 있는지 탐구해야 합니다.

---

5. Conclusion

저희는 토큰 간의 수치적 근접성을 고려함으로써 언어 모델이 수치 데이터를 처리하는 내재적 능력을 향상시키기 위한 새로운 접근법으로 숫자 토큰 손실(NTL)을 도입했습니다. 표준 교차 엔트로피 손실을 NTL로 보강함으로써, 저희는 추가적인 계산 오버헤드 없이 기존 아키텍처에 원활하게 통합되는 간단하면서도 효과적인 방법을 제공합니다.

저희의 실험은 인코더-디코더 및 디코더-전용 아키텍처 모두에서 NTL의 효과를 명백하게 입증했습니다. 수학, 산술, 추론과 관련된 여러 데이터셋에서의 실험 결과, 특히 특화된 숫자 임베딩이 없는 모델에서 수치적 추론 능력이 크게 향상되었습니다. 더 나아가, 회귀 데이터셋에 대한 저희의 결과는 NTL을 사용한 훈련이 토큰 헤드를 가진 언어 모델(LM)이 회귀 과제를 위해 특별히 설계된 모델과 경쟁할 수 있게 해준다는 것을 보여주었습니다. 또한 저희는 NTL이 독해와 같은 표준 텍스트 전용 과제에서의 능력을 저해하지 않음을 확인했습니다. 마지막으로, 어려운 GSM8k 데이터셋에서 30억(3B) 파라미터 모델에 성공적으로 적용함으로써 NTL의 확장성이 입증되었고, 이는 대규모 언어 모델(LLM)으로의 통합 가능성을 열어주었습니다.

제안된 두 가지 NTL 종류(NTL-WAS와 NTL-$L_p$) 중에서, NTL-WAS는 오차 상쇄로 인해 발생하는 NTL-$L_p$의 바람직하지 않은 지역 최솟값(local minima)을 피할 수 있으므로 더 선호되는 손실 함수입니다. 그러나 NTL-WAS와는 달리, NTL-$L_p$ 내부의 내적(dot product)은 원래 숫자 공간의 양을 산출하는데, 이는 여러 토큰을 통합하는 더 복잡한 손실을 계산하는 데 유용할 수 있습니다. 예를 들어, NTL의 현재 한계점 중 하나는 각 숫자 단위(digit-level) 토큰을 동등하게 중요하게 취급하여, 더 높은 자릿수를 가진 숫자의 더 큰 중요성을 무시한다는 것입니다. 이 한계는 손실을 숫자 단위가 아닌 숫자 수준(number level)에서 계산함으로써 해결될 수 있습니다. 예를 들어, 자릿수에 따른 단순한 스케일링을 적용하거나, NTL-$L_p$의 내적 아이디어를 활용하여 숫자 수준의 예측값을 계산하는 방식입니다.

더 나아가, 향후 연구는 추가적인 산술 특화 훈련 적응 기법과의 시너지 효과를 탐색하는 데 초점을 맞춰야 합니다. 특히 LLaMA나 Gemma와 같은 중대규모 오픈 소스 모델의 미세 조정을 통해 그 확장성과 일반화 잠재력을 추가로 평가하는 것은 매우 흥미로울 것입니다. 전반적으로, 이 접근법은 수치적으로 풍부한 영역에서 언어 모델을 향상시키는 실용적인 해결책을 제공하며, 수학 및 과학 분야에서 LM의 더 정확하고 신뢰할 수 있는 응용에 기여할 것입니다.