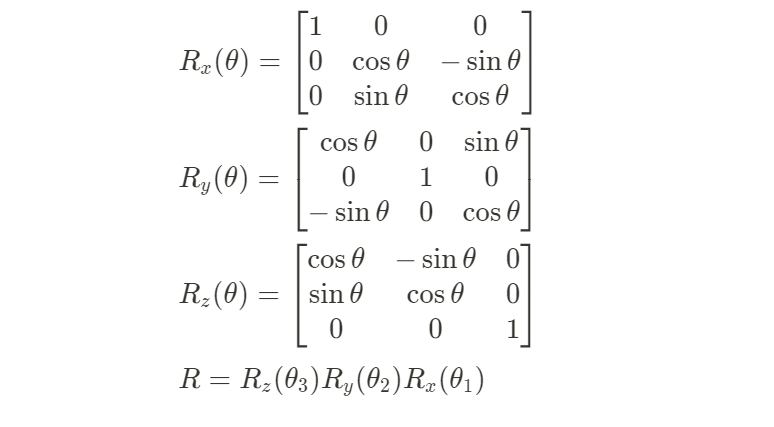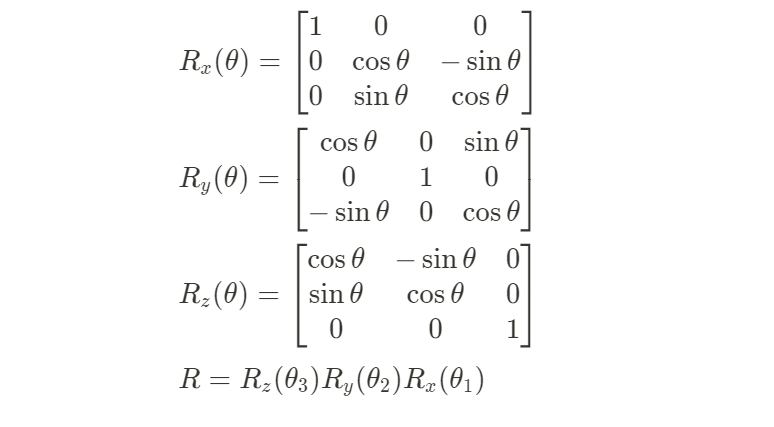1) Translation
⎣⎢⎡x′y′z′⎦⎥⎤=⎣⎢⎡xyz⎦⎥⎤+⎣⎢⎡txtytz⎦⎥⎤
2) Rotation
Rx(θ)=⎣⎢⎡1000cosθsinθ0−sinθcosθ⎦⎥⎤
Ry(θ)=⎣⎢⎡cosθ0−sinθ010sinθ0cosθ⎦⎥⎤
Rz(θ)=⎣⎢⎡cosθsinθ0−sinθcosθ0001⎦⎥⎤
R=Rz(θ3)Ry(θ2)Rx(θ1)
아래 식과 같이 일반화도 가능하다. 만약 Rx를 구하고자 한다면 (1,0,0)을 (l,m,n)에 대입하면 된다. 또한 X, Y, Z 축이 아니더라도 (21,21,0)과 같은 특수한 경우에도 (l,m,n)에 대입하면 계산이 가능하다.
R(θ)=⎣⎢⎡ll(1−cosθ)+cosθlm(1−cosθ)+nsinθln(1−cosθ)−msinθml(1−cosθ)−nsinθmm(1−cosθ)+cosθmn(1−cosθ)+lsinθnl(1−cosθ)+msinθnm(1−cosθ)−lsinθnn(1−cosθ)+cosθ⎦⎥⎤
1) Translation
⎣⎢⎢⎢⎡100001000010txtytz1⎦⎥⎥⎥⎤
2) Rotation
Rx=⎣⎢⎢⎢⎡10000cosθsinθ00−sinθcosθ00001⎦⎥⎥⎥⎤
3) Scaling
⎣⎢⎢⎢⎡Sx0000Sy0000Sz00001⎦⎥⎥⎥⎤
⎣⎢⎡x′y′z′⎦⎥⎤=⎣⎢⎡adgbehcfi⎦⎥⎤⎣⎢⎡xyz⎦⎥⎤+⎣⎢⎡txtytz⎦⎥⎤
⎣⎢⎢⎢⎡x′y′z′1⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡adg0beh0cfi0txtytz1⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡xyz1⎦⎥⎥⎥⎤