Louvain Clustering

Kyeonghun Jeong·2024년 6월 4일

Transcriptome

목록 보기

5/6

단일세포 전사체에서의 군집 분석 (Clustering Analysis)

단일세포 RNA 시퀀싱(scRNA-seq)은 개별 세포 수준에서 전사체의 발현 양상을 분석할 수 있는 강력한 도구입니다. 이를 통해 세포의 이질성 (heterogeneity) 과 희귀 세포 집단 (rare cell population) 을 발견할 수 있습니다. 그러나 수만에서 수십만 개의 세포로 이루어진 대규모 데이터를 분석하기 위해서는 효과적인 군집 분석 방법이 필수적입니다. 군집 분석을 통헤 데이터의 내재된 구조 (예: 세포 유형, 세포 상태, 발달 단계) 를 파악하고, 생물학적으로 의미 있는 세포집단을 구분할 수 있기 때문입니다.

군집 분석은 비슷한 특성을 가진 세포들을 그룹화하여 세포 유형을 구분 (cell type annotation)하고, 각 세포 집단의 특징을 파악 (Characterization) 하는데 사용됩니다. 널리 사용되는 군집 분석 방법으로는 K-means clustering, hierarchical clustering, graph-based clustering 등이 있습니다.

이 중에서 Louvain clustering 은 그래프 기반의 군집 분석 방법 중 하나로, 단일세포 시퀀싱 데이터 처리에 특화된 많은 패키지에서 지원하고 있습니다.

The standard approach to clustering single‐cell datasets has become multi‐resolution modularity optimization as implemented in the Louvain algorithm on single‐cell KNN graphs. ... It has been shown to outperform other clustering methods for single‐cell RNA‐seq data, and flow and mass cytometry data. (Moleculay systems biology, 2019)

Louvain clustering은 단일세포 데이터의 고차원적 구조를 효과적으로 반영할 수 있어 생물학적으로 의미 있는 결과를 도출하기에 적합한 방법으로 알려져 있습니다.

단일세포 전사체 분석에서 Louvain clustering이 효과적으로 사용될 수 있는 이유는 다음과 같습니다.

그래프 기반의 접근: 단일세포 데이터의 고차원적 특성을 그래프 구조로 표현함으로써 세포 간의 복잡한 관계를 효과적으로 모델링할 수 있습니다.
- 희소성 (Sparsity) 고려: 단일세포 RNA 시퀀싱 데이터는 대부분의 유전자가 발현하지 않는 희소성을 가지고 있어 노이즈가 많은 편입니다. Louvain clustering에서는 세포 간 유사도 기반으로 엣지를 구성하므로 이러한 희소성으로 인한 노이즈를 자연스럽게 제거할 수 있습니다. 특히, Louvain clustering을 수행하기 전에 주로 k-nearest neighbor (KNN) 그래프를 구성하는데, 이 과정에서도 희소성에 의한 노이즈의 영향이 추가적으로 완화될 수 있습니다. KNN 그래프에서는 각 세포와 가장 유사한 k개의 이웃 세포들 사이에만 엣지가 연결되기 때문입니다.
계층적 구조 탐색: Louvain 알고리즘은 다양한 해상도 (resolution)에서 계층적 커뮤니티 구조를 탐색할 수 있습니다. 이를 통해 단일세포 데이터에 내재된 세포 유형, 세포 상태 등의 계층적 구조를 효과적으로 파악할 수 있습니다.
확장성 (Scalability): Louvain 알고리즘의 계산 복잡도는 그래프의 엣지 수에 비례하므로 (O(N log N)), 대규모 단일세포 데이터셋에도 효과적으로 적용 가능합니다.

이러한 장점들로 인해 Louvain clustering은 단일세포 전사체 데이터 분석에 있어 강력하고 효과적인 도구로 자리매김하고 있습니다.

Louvain Clustering

Louvain clustering은 Seurat, Scanpy 등의 단일세포 분석 패키지에서 기본적으로 제공하는 군집 분석 방법 중 하나입니다. 이는 그래프 이론에 기반한 기법으로, 네트워크 구조를 분석하여 군집을 구분합니다.

Louvain clustering의 핵심 개념은 네트워크(=그래프) 내에서의 커뮤니티 탐지 (community detection) 입니다. Community란 그래프 내에서 서로 밀접하게 연결된 노드들의 집합을 의미합니다.

Louvain clustering은 모듈러리티(modularity)라는 척도를 최대화하는 방향으로 그래프를 분할하여 커뮤니티를 찾아냅니다. 모듈러리티는 동일한 커뮤니티 내의 노드들 사이의 연결 밀도와 서로 다른 커뮤니티 사이의 연결 밀도의 차이를 정량화한 값입니다. 모듈러리티가 클수록 커뮤니티 내의 연결은 많고, 커뮤니티 간의 연결은 적다는 것을 의미합니다.

그래프 / 네트워크

그래프 또는 네트워크는 객체 간의 관계를 표현하는 수학적 구조입니다. 그래프는 노드(node)와 엣지(edge)로 구성됩니다. 노드는 객체 를 나타내며, 엣지는 객체 간의 연결 관계 를 나타냅니다.

Louvain clustering을 적용하기 위해서는 단일세포 데이터를 그래프 형태로 표현해야 합니다. 단일세포 데이터의 경우 다음과 같이 그래프의 구성 요소와 대응시킬 수 있습니다.

노드 (node, vertex) : 개별 세포를 나타냅니다. 각 노드는 해당 세포의 유전자 발현 프로파일을 포함하고 있습니다.
엣지 (edge) : 두 세포 간의 연결 관계를 나타냅니다. 주로 k-nearest neighbor (KNN) 그래프를 사용하며, 이 경우 각 세포와 가장 유사한 k개의 이웃 세포들 사이에 엣지가 연결됩니다.
엣지 가중치 (edge weight) : 엣지에 할당된 숫자 값으로, 보통은 연결 강도 또는 연결의 중요도 를 나타냅니다. KNN 그래프에서는 보통 가중치 없는 그래프(unweighted graph)를 사용하므로, 초기에는 모든 엣지의 가중치가 1로 동일하게 설정됩니다. 그러나 Louvain 알고리즘의 수행 과정에서 커뮤니티를 기반으로 새로운 네트워크를 구성할 때, 엣지 가중치가 변경됩니다. 이때 엣지 가중치는 커뮤니티 간 연결 갯수를 나타내게 됩니다.

이렇게 구성된 그래프는 단일세포 데이터의 고차원적 구조를 간결하게 표현할 수 있으며, Louvain clustering을 비롯한 다양한 그래프 기반 알고리즘을 적용할 수 있는 기반이 됩니다.

모듈러리티 (Modularity)

모듈러리티는 다음과 같은 수식으로 정의됩니다:

Q = \sum_{i=1}^{n_C} \left[ \frac{1}{2M} \sum_{i, j \in C_i} \left( a_{ij} - \frac{k_i k_j}{2M} \right) \right]

여기서:

$n_C$ 는 커뮤니티의 수
$C_i$ : $i$ 번째 커뮤니티
$i, j$ 는 노드 번호
$a_{ij}$ 는 $i$ 와 $j$ 간의 엣지 가중치
$k$ 는 한 노드의 엣지 가중치 합
$M$ 은 모든 엣지 가중치의 합

이 수식은 커뮤니티 내의 엣지 가중치 합이 임의의 엣지 가중치 기대값에 비해 얼마나 큰지를 측정합니다.

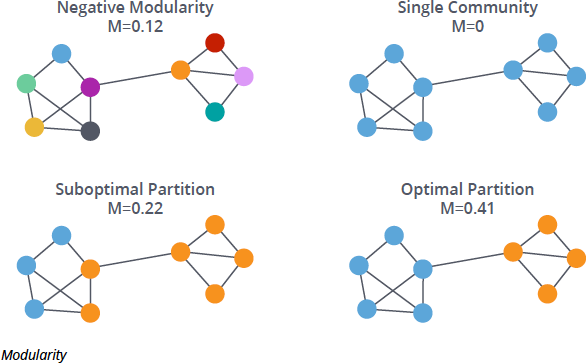(출처)

Negative modularity (좌상단 그림):

모든 노드들이 개별적인 커뮤니티에 속해 있어, 커뮤니티 내 연결이 없습니다. 서로 다른 커뮤니티 간의 연결만 존재합니다.

Single community (우상단 그림) :

모든 노드가 동일한 커뮤니티에 속해 있어, 커뮤니티 간의 차이가 전혀 없습니다.

Suboptimal partition (좌하단 그림):

두 개의 커뮤니티로 분할되어 있습니다. 주황색 커뮤니티 내 제일 좌측 노드 두 개는 주황색 커뮤니티 내에서의 연결보다 파란색 노드, 즉 타 커뮤니티에 속하는 노드와의 연결이 더 많습니다.

Optimal partition (우하단 그림):

노드들이 두 개의 명확한 커뮤니티로 분할되어 있습니다. 각 커뮤니티 내의 노드들이 밀접하게 연결되어 있으며, 커뮤니티 간의 연결은 적습니다.
파란색 노드와 주황색 노드는 각각의 커뮤니티 내에서 많은 연결을 가지고 있고, 서로 다른 커뮤니티 간의 연결은 최소화되어 있습니다.

Louvain 알고리즘

Louvain algorithm은 다음과 같은 과정을 통해 그래프를 분할합니다.

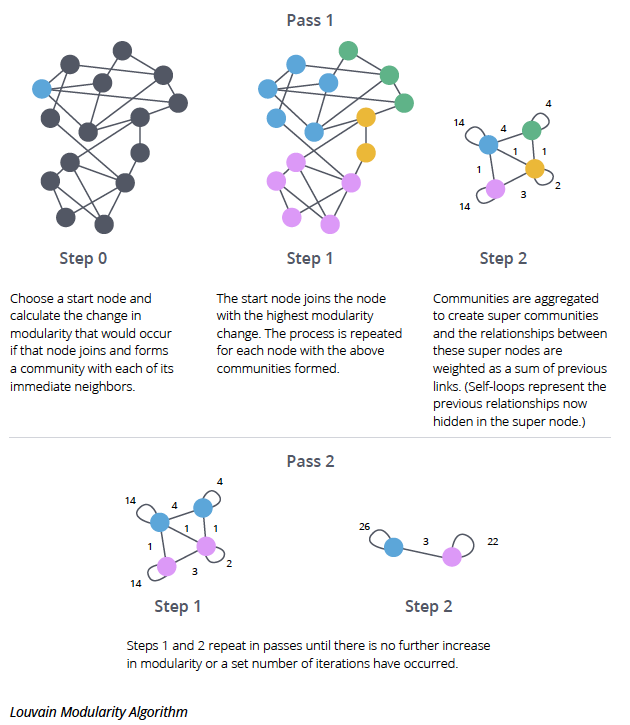(출처)

Pass 1:
- Step 0: 초기에는 1 노드는 1 커뮤니티로, 각 노드가 독립된 커뮤니티를 형성합니다.
- Step 1: 각 노드에 대해 이웃 커뮤니티 (neighbor community)로 이동했을 때의 modularity 변화량을 계산하고, 가장 큰 증가를 보이는 커뮤니티로 노드를 이동시킵니다.(=해당 이웃 커뮤니티로 속하게 만듭니다.) 이 과정을 modularity 가 더 이상 증가하지 않을 때까지 반복합니다.
- Step 2: Step1에서 얻어진 커뮤니티를 기반으로 새로운 네트워크(new network)를 만듭니다. 각 커뮤니티가 노드가 되며, 커뮤니티 간 연결 갯수 (edge 수) 가 new network의 edge 가중치가 됩니다. 커뮤니티 내에서의 연결 갯수는 self-loop (자기 자신을 연결하는 edge)로 표현된 edge의 가중치가 됩니다.
Pass 2 (초그래프 기반)
- Step 1: New network (Pass 1의 Step 2 결과) 에 대해 Step 1, 2 과정을 반복하여 더 큰 커뮤니티를 형성합니다. Modularity 증가가 없을 때까지 반복합니다.
- Step 2: Step 1의 결과로 얻어진 커뮤니티를 기반으로 다시 new network를 만듭니다.

이러한 반복 과정을 통해 최종적으로 modularity 를 최대화하는 커뮤니티 구조를 얻을 수 있습니다.

마치며

Louvain clustering은 단일세포 RNA 시퀀싱 데이터의 생물학적 정보를 잘 반영하면서도 계산량이 적어 대규모 데이터에 적용하기 적합한 군집 분석 기법입니다. 또한 사전에 군집의 수를 지정할 필요가 없어 탐색적 분석에 유용합니다.

그러나 최적의 군집 수를 찾기 어려울 수 있다는 단점이 있습니다. 따라서 연구자는 Louvain clustering의 결과를 비판적으로 해석하고, 다양한 평가 지표와 시각화 방법을 활용하여 신중하게 군집의 수와 생물학적 의미를 판단해야 할 것입니다.

louvain clustering의 문제점들을 몇가지 개선한 leiden clustering (ref)이라는 알고리즘이 제안되었으며, 이 알고리즘은 scanpy 에서 군집 분석에서 기본값으로 설정되어 있습니다. (Seurat 의 경우 Louvain clustering이 기본값입니다.)
출처