AE(Autoencoders)에 대해 알아보겠습니다.
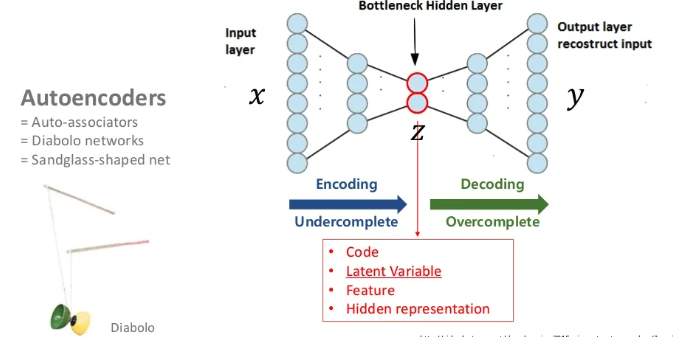
AE는 기본적으로 입력과 출력이 같게되는 구조입니다. AE의 가장 큰 목적은 이전 시간에 배운 Manifold Learning이 목표라는 것을 기억합시다. 위 이미지의 값은 Code, Latent variable, Feature, Hidden representation 등 다양하게 불립니다.
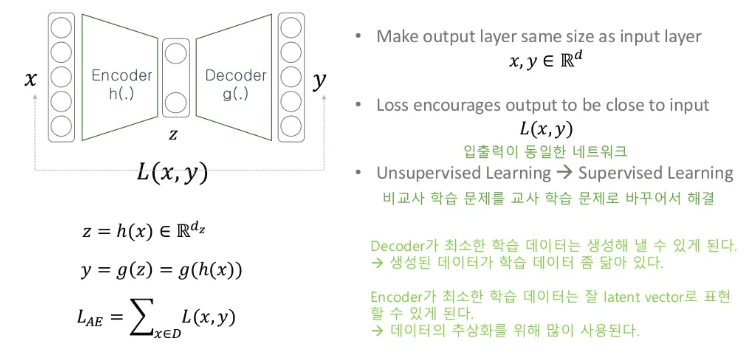
입력의 와 출력의 값을 이용해 Loss를 구하게 됩니다. 결국 와 값이 같아져야 하는데 이렇게 학습을 하게 되면 어떤 이점이 있을까요?
지난 시간에 AE는 dimentionality reduction을 한다고 했습니다. 만약 사람에게 10만차원을 2차원으로 줄여보라고 했을때 굉장히 난감할 수 있습니다. 하지만 학습이 잘된 AE가 있다면 직관적으로 encoder가 입력값 를 저차원의 로 압축을 잘했다고 생각할 수 있습니다. decoder는 어떤 라는 벡터로 라는 데이터를 생성하는 모델입니다. 이 decoder는 고정된 입력값에 대하여 고정된 출력을 만들도록 학습되는 특징 때문에 성능이 좋지 않다고 생각할 수 있지만 반대로 최소한 이 정도의 성능은 보장이 된다고 볼 수 있습니다.
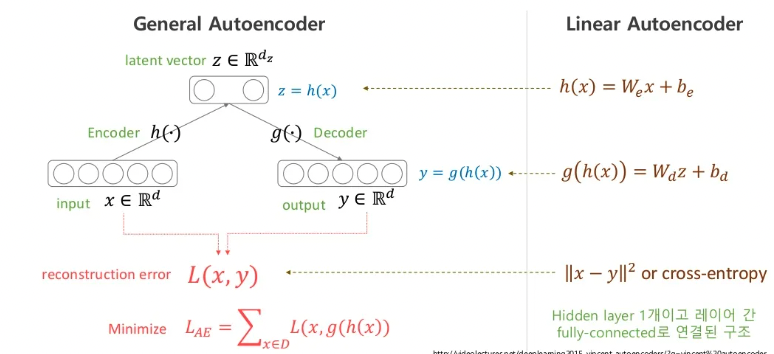
Linear AE는 activation function 없이 사용한 모델을 말합니다. 단순히 여러번의 가중치를 곱하고 편향을 더하는 행동은 결국 어느정도의 가중치를 곱하고 편향을 더한것과 같은 결과입니다. x에 1을 10번 더하는 것과 10을 한번 더하는 것을 결과가 같으니까요.

Linear AE를 설명드린 이유는 이 모델에 MSE를 사용하게 되면 똑같은 manifold(sub-space)를 학습하게 된다는 논문이 있습니다.
사실 AE의 구조는 이게 전부입니다.
DAE
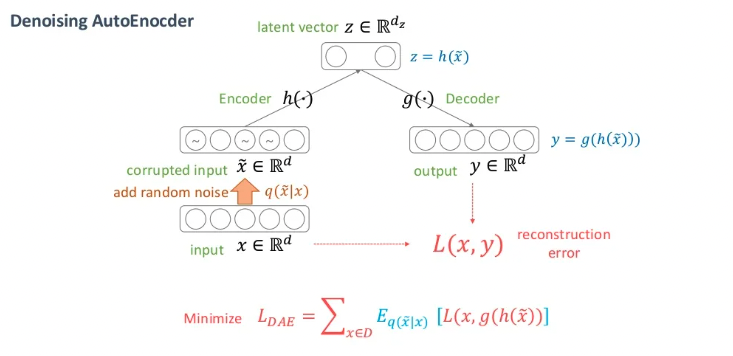
DAE와 AE와의 차이는 입력값 에 노이즈를 추가한 것을 사용한다는 것입니다. 이렇게 노이즈된 값을 사용했을 때 온전한 값이 나오길 기대하기 때문에 denosing이라는 용어를 사용합니다.
AE의 목적인 manifold learning은 feature를 잘 찾겠다는 의미입니다. 예를 들어 하나의 사람 이미지에 사람이라는 의미를 변질시킬 정도가 아닌 약간의 노이즈를 추가한다고 해봅시다. manifold의 영역인 로 갔을 때 노이즈된 사람 이미지는 결국 사람 데이터가 있는 분포에 다가가야 합니다. 이런 아이디어를 기대하며 학습시키는 방법이 DAE입니다.

CAE

CAE를 설명하기 앞서 SCAE를 살펴보겠습니다. Loss function을 보시면 기존 AE와 같이 입력값과 온전한 입력값에 대한 출력값의 loss인 reconstruction error를 사용합니다. 여기까진 AE와 동일하지만 DAE에서와 같은 의미로 인코딩 된 x와 corrupted된 x사이의 거리가 같아지길 기대하는 Stochastic Regularization로 추가되어 있습니다.

위의 SCAE식을 좀 더 결정적으로 정리된게 CAE입니다. 잘 사용되지 않지만 자세한 내용을 알고싶은 분들은 논문을 살펴보길 바랍니다.
오늘은 이렇게 Autoencoders에 대해서 알아보았습니다. AE는 Manifold learning에 목적이 있다는 것을 기억하면서 다음은 VAE(Variational Autoencoders)에 대해서 알아보겠습니다.