이번에는 Dimentionality reduction이라고도 불리는 manifold learning에 대해서 알아보겠습니다.
Mainifold를 설명하려면 고차원 데이터부터 시작하게 됩니다.
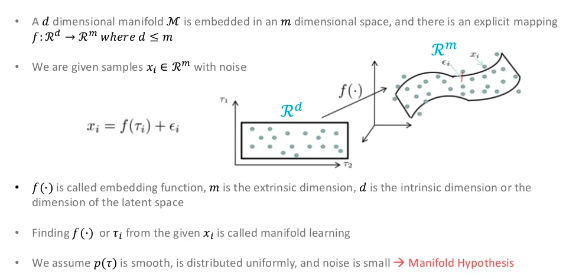
위의 이미지는 시각화를 위해 고차원 데이터(3차원)을 저차원(2차원)으로 줄이는 것에 대한 설명입니다. 실제로 사용되는 고차원은 수만 차원의 데이터를 저차원으로 만드는 것이라고 생각하시면 됩니다.
이런 고차원 데이터의 train data를 한 공간에 점으로 표현할 수 있습니다. 여기서 manifold란 "train data를 잘 설명할 수 있는 sub-space"를 의미합니다.
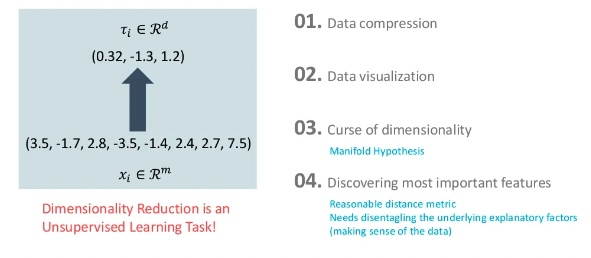
정의가 어려울 수 있지만 결론적으로 데이터를 적절한 차원으로 줄이는 착원축소라는 것이죠.
이렇게 해서 얻는 이점은 아래와 같습니다.
- Data compression
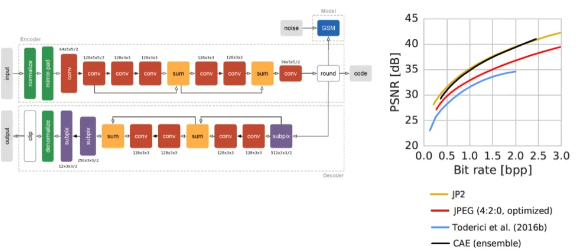
- Data visualization

- Curse of dimensionality
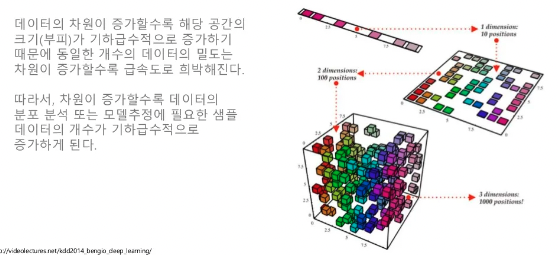
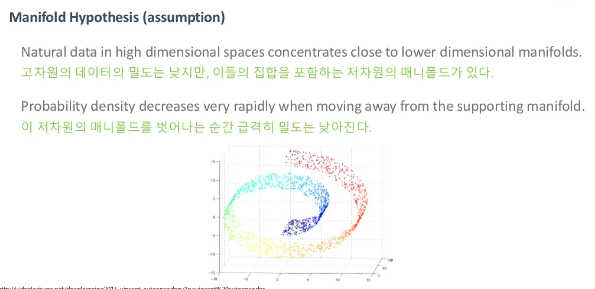
차원의 저주를 해결하기 위해 manifold를 사용하기도 합니다.
차원이 증가할수록 해당 공간을 표현할 train data가 기하급수적으로 필요하게 되는데 manifold의 정의와 같이 어떤 공간을 잘 설명할 수 있는 서브 공간이 있다면 이 문제를 해결할 수 있겠죠. 그렇다면 진짜 그런 공간이 있는지 이미지 분야에서 직관적으로 알아보겠습니다.

200x200의 RGB 채널을 가진 이미지 공간이 있다고 하겠습니다. 만약 이 공간에 적절하게 데이터들이 분포되어 있다면 어떨까요? uniform하게 값을 가져오면 그럴싸한 이미지가 만들어져야 하지 않을까요? 실제로 실험을 해보면 알 수 없는 노이즈만 생성되게 됩니다. 실험적으로 데이터를 잘 설명한 특정 영역이 존재한다는 것을 알 수 있습니다.
- Discovering most important features
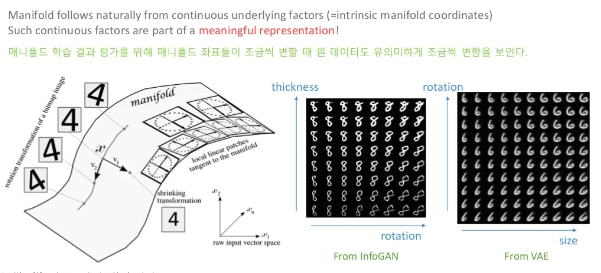
manifold를 잘 찾았다는 것은 중요한 feature들을 가지고 있다는 뜻입니다.
위 이미지에서 축을 따라 올라가니 rotation이 되는 것을 확인할 수 있습니다. 저희는 rotation에 관련된 feature를 찾은 것이죠.
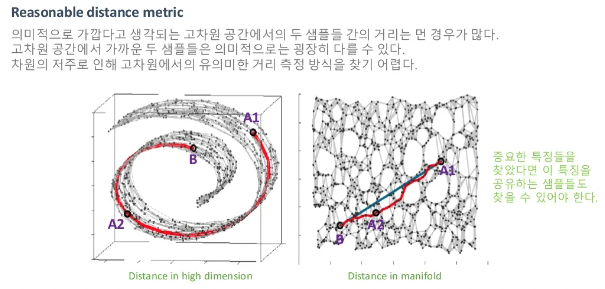
feature를 잘 찾는다는 것은 distance metric으로도 볼 수 있습니다.
위 이미지의 왼쪽 공간에서 B로부터 2개의 샘플들간의 유클리드 거리를 구해보면 A2보다 A1이 더 가깝게 됩니다. 하지만 dimentionality reduction을 통해 다시 유클리드를 계산해보면 A2가 더 가까운것을 확인하실 수 있습니다. 이 manifold상의 거리가 의미적으로 훨씬 중요한 정보를 가지고 있다는 것을 아래의 예시를 통해 알아보겠습니다.
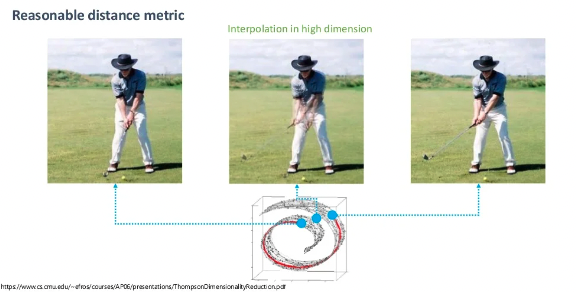
우리는 맨 왼쪽사진과 맨 오른쪽사진 중간과정의 데이터를 구하고 싶다고 해봅시다.
포인트들의 평균값을 구해 데이터를 추출했을때 위의 중간 사진처럼 두 사진이 애매하게 합성된 사진이 나오게 됩니다. 우리가 원하는 결과는 이게 아닌데 왜 이런 현상이 일어날까요? 바로 manifold 공간을 벗어났기 때문입니다. 처음 설명한것과 같이 manifold의 공간을 벗어나게 되면 데이터 밀도가 낮게 되고 우리가 흔히 볼 수 있는 이미지가 아니기 때문입니다. 반대로 다른 예시를 보겠습니다.
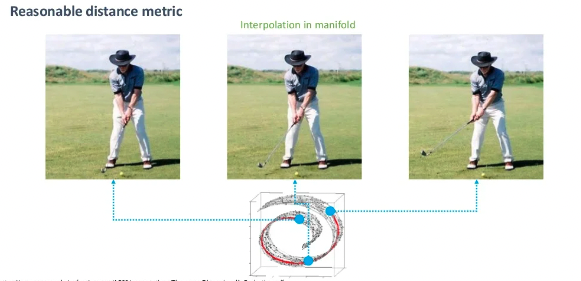
위 처럼 manifold상의 중간의 샘플을 찾게 되면 의미적으로 우리가 원하는 데이터를 얻을 수 있습니다.
방법론
Auto-Encoder 말고도 다양하게 Dimensionality Reduction과 density estimation을 하는 방법론에 대해서 알아보겠습니다.

PCA
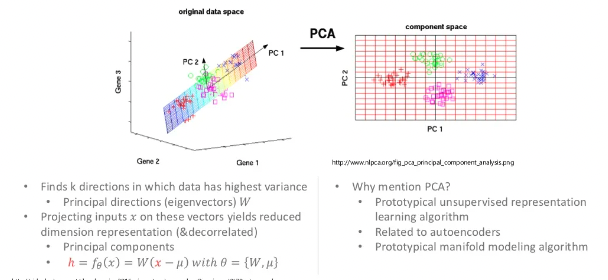
PCA는 원 데이터를 샘플 공간에 뿌려보고 분산이 최대치가 되는 축을 찾아 점차 차원을 축소해 나가는 방법입니다.
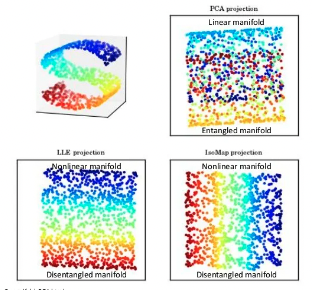
PCA는 Linear한 방법이기 때문에 원 데이터가 꼬여있는 형태일 경우 잘 구분하지 못하는 문제가 있습니다.
Isomap, LLE
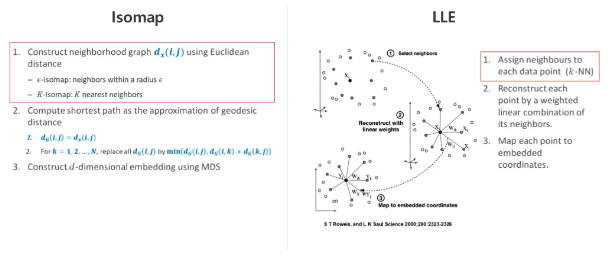
Non-Linear 방법인 Isomap과 LLE의 공통점은 각 샘플별로 이웃한 값을 구하는 과정이 있습니다.
이 작업이 필요한 이유는 원 데이터에서 이 만큼 가까운 데이터는 manifold상에서도 가깝다라는 가정하기 때문입니다.
Parzen windows(Density Estimation 방법)
dimentionality reduction과 같이 density estimation에도 기존 방법론이 있습니다.
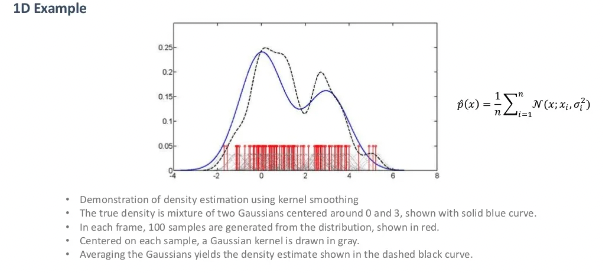
Parzen windows는 각 샘플에 가우시안 커널을 사용해 확률분포를 모델링하는 방법이다.
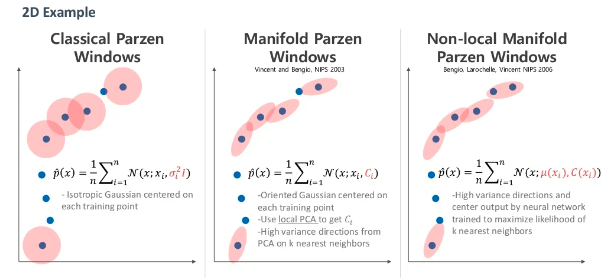
이 방법도 위와 같이 발전되어 왔습니다.
마지막으로 Auto-Encoder도 dimentionality reduction, density estimation을 하는데 기존의 방법과 뭐가 다를까요?

위에서 설명드린 기존의 방법론은 전부 Neighborhood 기반입니다.
이 Neighborhood 기반이 어떤 문제가 있을까요? 이 글의 처음부터 했던 이야기는 공간상의 가까운 포인트들이 의미적으론 가깝지 않을 수 있다는 것입니다. 위의 기존 방법론들은 단순히 이웃한 데이터들을 가지고 접근한 방법이기 때문에 데이터가 고차원일수록, sparse할수록 문제가 생길 수 있습니다.
다음시간에는 드디어 Auto-Encoder에 대해서 알아보겠습니다.