[Paper] DoRA

논문 : DoRA: Weight-Decomposed Low-Rank Adaptation

Background

• PEFT : parameter-efficient fine-tuning으로 효율적으로 모델을 fine-tuning할 수 있는 방법론

• LoRA : PEFT 중 하나의 기법으로, 사전학습 된 가중치는 freeze하고 low-rank로 가중치를 분해하여 학습하는 방식

• Full Fine-Tuning(FT) : 모델의 전체 파라미터를 업데이트하는 방식

Problem state

• LoRA와 같은 기법으로 큰 모델을 효율적으로 fine-tuning할 수 있지만, FT와의 격차는 여전히 존재함

Contribution

• 새로운 PEFT 기법인 DoRA를 소개하고 inference latency 없이 FT와 유사한 성능을 보임

• 기존의 FT, PEFT와 달리 새로운 가중치 분해 방법을 소개함

• 결과적으로, LoRA를 능가하는 성능을 보여줌

Method

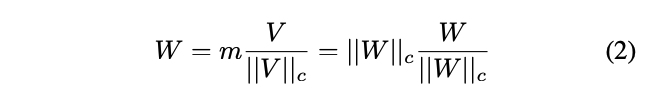
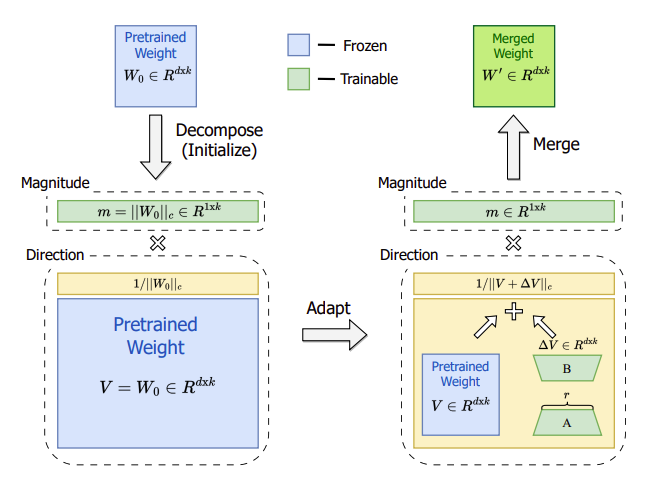
• 본 논문에서는, magnitude와 direction 두 가지의 matrix로 분해한 구조를 사용함.

• m은 magnitude vector로 1 x k의 차원을 가지고, V는 directional matrix로 d x k 차원을 가짐.

• $||\cdot||_c$는 각 column의 vector-wise norm을 의미함

• $V/||V||_c$로 각 열의 방향을 유지하고 m으로 그 크기를 정렬

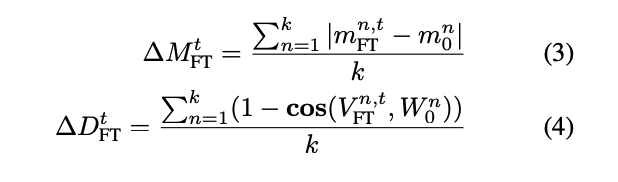
• $\Delta{M}_{FT}^t$는 사전학습 된 W와 fine-tuning한 W간의 크기 차이를 표현

• $\Delta{D}_{FT}^t$는 사전학습 된 W와 fine-tuning한 W간의 방향 차이를 표현

• $m_{FT}^{n,t}, m_0^n$은 magnitude vector들의 n번째 값을 나타냄

• $V_{FT}^{n,t}, W_0^n$는 $V_{FT}^t, W_0$의 n번째 column을 나타냄

• 위의 수식을 토대로 $W_{LoRA}, W_0$의 차이도 계산 되어짐

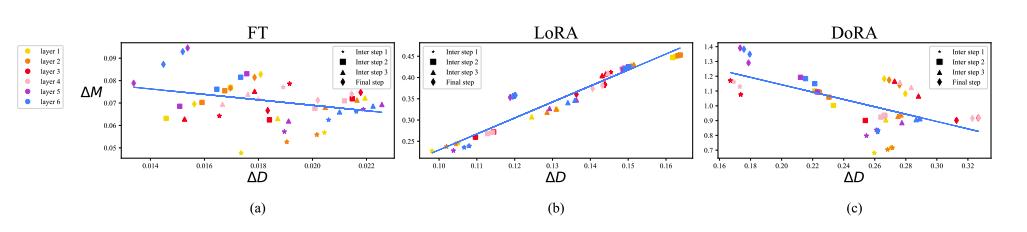
• LoRA는 모든 steps에서 양의 기울기 추세를 보이는 반면, FT는 음의 기울기 추세를 보이고 있음

• 이런 패턴을 이유로, LoRA는 미세한 조정 능력이 부족함

• 본 논문에서는, LoRA가 크기와 방향을 동시에 학습하는 것은 너무 복잡하기 때문에 방향에 대해서만 집중하도록 제한하고 크기 component를 조정할 수 있도록 허용하는 것은 기존 접근법 보다 더욱 단순화 될 수 있다고 함.

• 또한, 방향을 학습하는 것은 가중치 분해를 통해 더욱 안정적으로 만들 수 있음.

• 이런 아이디어와 weight normalization 논문의 영감을 받아 DoRA를 제안함. weight normalization과의 차이점은 from scrath부터 학습하는 반면, DoRA는 pre-trained weight를 사용함

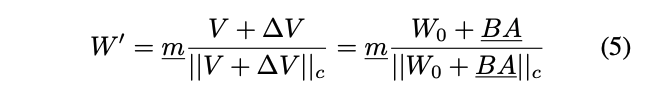
• directional component는 LoRA를 사용해서 더욱 효율적으로 학습하도록 함.

• 위의 수식에서 underline된 항만 학습하는 파라미터임

• DoRA는 FT와 비슷한 음의 기울기 추세를 보이며, 비교적 최소한의 크기 변화로 상당한 방향성 조정이 가능하고 LoRA보다 FT에 더 가까운 학습 패턴을 보임

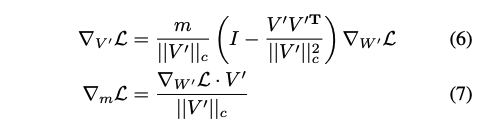
• 위의 수식은 Gradient of Loss로 (5)번 식(V'로 치환)으로부터 유도됨

• (6)번 식에서 $\nabla_{W'}L$을 $\frac{m}{||V'||_c}$로 스케일링하고 현재 가중치 행렬에서 멀리 떨어져 projected 되는 것을 보여줌. 이로 인해 공분산 행렬을 항등 행렬과 가깝도록 하여 최적화에 유리하게 함. 자세한 내용은 Weight Normalization 참고

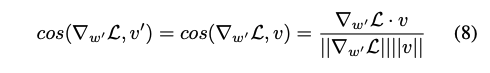
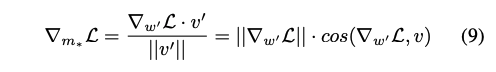
• $v, w'$는 최초로 $w_0$으로 초기화 되어지기 때문에 위와 같이 (7)번식을 다시 쓸 수 있음

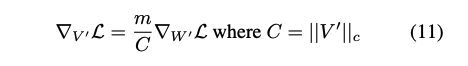
• 역전파시 추가적인 메모리 사용량을 줄이기 위해 (5)번 식의 $||V+\Delta V||_c$를 위와 같이 상수로서 처리함. LLaMA는 약 24.4% VL-BART는 약 12.4% 메모리 사용량을 줄이고 정확도는 유지할 수 있었음

Result

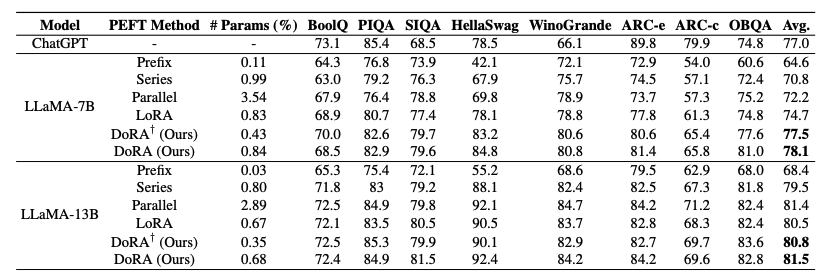
• 다양한 PEFT기법들과 비교하여 commonsense reasoning 데이터셋에 대해 DoRA가 좋은 성능을 보여줌.

• 이 외에도, Image/Video-Text Understanding, Visual Instruction Tuning 영역에서도 기존 PEFT보다 뛰어난 성능을 보여주면서, FT와는 유사하거나 뛰어난 성능을 보여줌

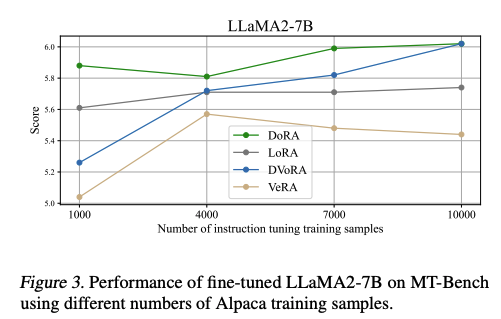
• 적은 sample 수에서도 성능을 유지하는 현상을 나타냄

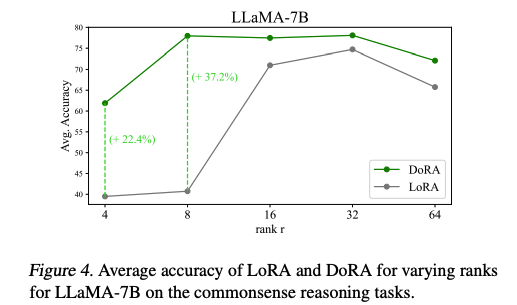
• rank의 변화에도 LoRA보다 뛰어난 robustness를 확인할 수 있음

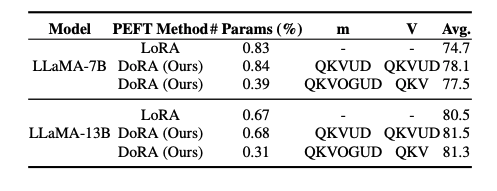
• target modules에 따른 성능도 DoRA가 우세한 것을 확인할 수 있음

Conclusion

• FT의 학습 추세와 유사한 새로운 가중치 분해 방법을 소개함

• 기존의 PEFT기법들에 비해 더 뛰어나며, FT와 비교할만한 성능을 보여줌