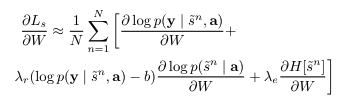[Paper] Show, Attend and Tell

hyunsooo·2024년 8월 7일

Paper

논문 링크 : Show, Attend and Tell: Neural Image Caption Generation with Visual Attention

Background

captioning : 이미지에 대한 설명을 하는 task
attention(in encoder-decoder architecture) : encoder의 특정 부분에 집중하여 decoding하는 기법

Problem state

Convnet의 최상위 layer의 표현으로 이미지 정보를 사용하는 것은 정보 손실의 원인이 될 수 있음

Contribution

Attention을 적용한 caption(soft/hard) 제안
attention을 통해 어디에, 무엇을 집중하는지 시각화하여 보여줌
caption generation을 정량적으로 평가하여 SOTA 달성

Method

bold체는 vector, captial 체는 matrix를 의미
본 논문의 모델은 하나의 raw image와 encoding된 단어 1-of-K의 sequence로 인코딩 된 caption y를 사용

y = \{\bold{y_1}, ..., \bold{y_c}\}, \bold{y_i} \in \mathbb{R}^K \newline K = \text{size of vocabulary} \newline C = \text{length of the caption}

ENCODER: Convolutional Features

feature vector를 추출하기 위해 CNN을 사용하고, extractor는 image의 각 부분을 D차원을 가진 L개의 vector를 생산

a = \{\bold{a_1},...,\bold{a_L}\}, \bold{a_i} \in \mathbb{R}^D

2D image 부분과 feature vectors 사이의 관련성을 얻기 위해, fully connected layer를 사용했던 이전 연구와는 달리 lower convolutional layer에서 feature를 추출함

$\bold{a_i}$ 는 annotation vector로 이전 연구의 feature vector와 동일한 의미이다.

DECODER: Long Short-Term Memory Network

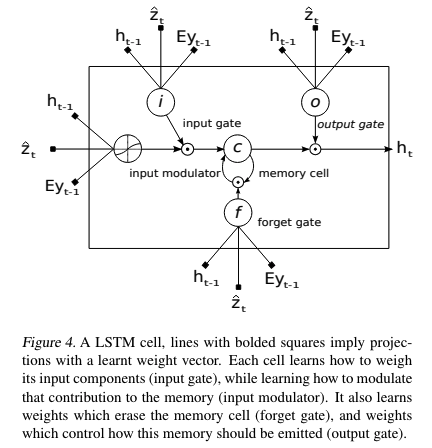
Decoder로는 LSTM을 사용하고 아래의 수식에서 $i, f, c, o, h, \hat{z}$ 는 각각 LSTM의 input, forget, memory, output, hidden state, 입력 image의 특정 위치 정보가 담긴 context vector를 의미함

\left( \begin{matrix} \bold{i_t} \\ \bold{f_t} \\ \bold{o_t} \\ \bold{g_t} \end{matrix} \right) = \left( \begin{matrix} \sigma \\ \sigma \\ \sigma \\ \text{tanh} \end{matrix} \right) T_{D+m+n,n} \left( \begin{matrix} \bold{Ey_{t-1}} \\ \bold{h_{t-1}} \\ \bold{\hat{z}_{t}} \end{matrix} \right) \newline \bold{c_t = f_t \odot c_{t-1} + i_t \odot g_t} \newline \bold{h_t} = \bold{o_t \odot \text{tanh}(c_t)}

$E \in \mathbb{R}^{m \times K}$ 는 embedding matrix, $m, n$ 은 embedding과 LSTM의 차원, $\sigma, \odot$ 은 sigmoid activation과 element-wise multiplication을 의미함

LSTM의 $c_0, h_0$ 는 아래와 같은 초기값을 사용

c_0 = f_{\text{init},c} (\frac{1}{L} \sum_{i}^{L} \bold{a_i}) \newline h_0 = f_{\text{init},h} (\frac{1}{L} \sum_{i}^{L} \bold{a_i})

Hard vs. Soft Attention

attention model ( $f_{att}$ )의 2가지 메카니즘

Hard Attention

annotation vector가 one-hot encoding으로 표현되는 것. 즉, 이미지의 여러 픽셀 중 하나의 영역에 집중
$s_{t,i}$ 는 t시점에서의 i번째(14x14 라면, 196) 픽셀에 대한 one-hot encoding 값을 나타냄, 이때 1이 되는 확률 값은 attention score( $\alpha_{t,i}$ )가 사용됨

e_{ti} = f_{att}(\bold{a_i}, \bold{h_{t-1}}) \newline \alpha_{t,i} = \frac{\text{exp}(e_{ti})}{\sum_{k=1}^L \text{exp}(e_{tk})} \newline p(s_{t,i} = 1 | s_{j < t}, \bold{a}) = \alpha_{t,i}

$s_{t,i}$ 는 a와 곱하여 attention 결과로 사용할 수 있고 아래와 같이 표현할 수 있음

\hat{z}_t = \sum_i s_{t,i}a_i

loss function : image features(a)에 대해 caption(y)의 log likelihood를 최대화

L_s = \sum_s p (s|\bold{a}) log p(y|s,\bold{a}) \leq log \sum _s p(s|\bold{a}) p(\bold{y}|s, \bold{a}) \newline = log p (\bold{y}|\bold{a})

위의 식에서 lower bound인 부분을 loss로 사용하고 W에 대해서 미분하면 아래와 같이 쓸 수 있음

\frac{\partial L}{\partial W} = \sum_s \bigg[ p(s|\mathbf{a}) \frac{\partial \text{log}p(\mathbf{y}|s, a)}{\partial W} + \text{log} p(\mathbf{y}|s,a) \frac{\partial p(s|\mathbf{a})}{\partial W}\bigg] \newline = \sum_s \bigg[ p(s|\mathbf{a}) \frac{\partial \text{log}p (\mathbf{y}|s,a)}{\partial W} + \text{log} p (\mathbf{y}|s,a) \cdot p(s|\mathbf{a}) \frac{\partial \text{log}p(s|a)}{\partial W} \bigg] \newline = \sum_s p(s|\mathbf{a}) \bigg[ \frac{\partial \text{log} p(\mathbf{y}|s, a)}{\partial W} + \text{log} p(\mathbf{y}|s,\mathbf{a}) \frac{\partial \text{log}p(s|a)}{\partial W} \bigg]

Monte Carlo Estimation을 적용하여 다시 작성할 수 있음. $\tilde{s}_t$ 는 multinoulli distribution에서 N개를 sampling하는 의미.

\tilde{s}_t \sim \text{Multinoulli}_L(\{\alpha_i\}) \newline \frac{\partial L_s}{\partial W} \approx \frac{1}{N} \sum_{n=1}^N \bigg[ \frac{\partial \text{log}p(\mathbf{y} | s^{\sim n} ,\mathbf{a})}{\partial W} + \text{log}p(\mathbf{y} \ s^{\sim n}, \mathbf{a}) \frac{}{}\bigg]

Monte Carlo estimator를 사용할 때 커지는 분산을 줄이기 위해 moving average를 사용함

b_k = 0.9 \times b_{k-1} + 0.1 \times \text{log} \space p(\mathbf{y}|\tilde{s}_k, \mathbf{a})

추가적으로 분산을 더 줄이기 위해 $\text{H}[s]$ (entropy term)을 추가
최종 loss function

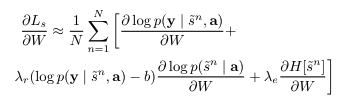
$\lambda_r, \lambda_e$ 는 exponential moving average와 entropy term의 비율을 타나내는 파라미터
0.5 확률로 $\tilde{s}$ 의 값을 $\alpha$ 로 사용

Soft Attention

Hard Attention에서는 매 time마다 $s_t$ 를 sampling 해서 사용하지만 Soft Attention에서는 $\hat{z}_t$ 를 사용함

\mathbb{E}_{p(s_t|a)}[\hat{z}_t] = \sum_{i=1}^L \alpha_{t,i} \mathbf{a}_i

hard attention에서는 $\alpha$ 가 가장 높은 값 하나(one-hot)를 사용 했지만, soft attention에서는 $\alpha$ 자체를 $a_i$ 에 곱하여 사용
k번째 word를 예측 하기 위해 normalized weighted geometric mean을 정의

\text{NWGM}[p(y_t = k | \mathbf{a})] = \frac{\Pi_i \text{exp}(n_{t,k,i})^{p(s_{t,i}=1|a)}}{\sum_j \Pi_i \text{exp}(n_{t,j,i})^{p(s_{t, i}=1|a)}} \newline \quad \quad \quad \quad \quad \quad \quad = \frac{\text{exp}(\mathbb{E}_{p(s_t|a)}[n_{t,k}])}{\sum_j \text{exp}(\mathbb{E}_{p(s_t|a)}[n_{t,j}])}

$\mathbb{E}[\bold{n_t}] = \bold{L}_o(\bold{Ey_{t-1}} + \bold{L}_h) \mathbb{E}[\bold{h}_t] + \bold{L}_z \mathbb{E}[\hat{\bold{z}_t}]$ , 즉, LSTM의 output gate를 통과한 값을 의미

Doubly Stochastic Attention

doubly stochastic attention은 $\sum_i \alpha_{t,i} =1$ 이 되도록 하면서 규제항( $\sum_t \alpha_{t,i} =1$ )도 추가하여 학습
쉽게 말해 196개의 픽셀들의 score가 1이 되록하면서, caption의 time 별로의 pixel score도 1이 되도록 학습하는 것
이론적으로 모든 time 별로의 픽셀의 합이 1이 되는 것은 불가능 하지만 1이 되도록 규제를 하는 것
regularization loss

\lambda \sum_i^P(1-\sum_t^Ta_{t, i})^2

최종 loss

L_d = -\text{log}(P(\mathbf{y}|\mathbf{x})) + \lambda \sum_i^P(1-\sum_t^Ta_{t, i})^2

Results

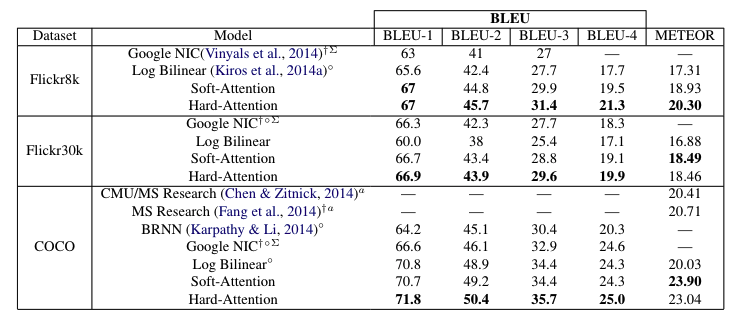
hard attention이 soft attention보다 좋은 성능을 보여줌

Conclusion

기존 caption 프로세스에 attention을 추가하여 SOTA 달성

hyunsooo

지식 공유

이전 포스트

[Paper] Context Embeddings for Efficient Answer Generation in RAG

다음 포스트

[Paper] Show, Attend and Tell

Background

Problem state

Contribution

Method

ENCODER: Convolutional Features

DECODER: Long Short-Term Memory Network

Hard vs. Soft Attention

Hard Attention

Soft Attention

Doubly Stochastic Attention

Results

Conclusion

[Paper] Context Embeddings for Efficient Answer Generation in RAG

Llama 모델링 분석

0개의 댓글