Revisit Deep Neural Networks

이 내용은 오토인코더의 모든 것의 강의를 정리한 내용입니다.

오토인코더(AutoEncoder)는 입력과 출력이 동일한 값을 가지도록 만드는 구조를 말합니다.
오토인코더의 핵심 키워드는 아래와 같습니다.

1. Unsupervised Learning

2. Manifold Learning

3. Generative model Learning

4. ML(Maximum Likelihood) density estimation

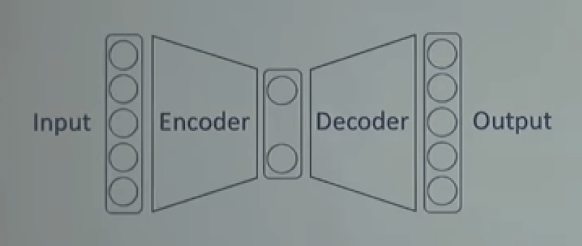
인코더는 차원을 축소하는 역할을 합니다. 이 역할을 Dimentionality reduction, manifold learning이라고 부릅니다.
디코더는 어떤 벡터를 이용해 데이터를 만드는 생성 역할을 합니다.
자세한 내용을 전하기 전 이번 포스트는 Deep Neural Network에 대해 정리하고 가겠습니다.

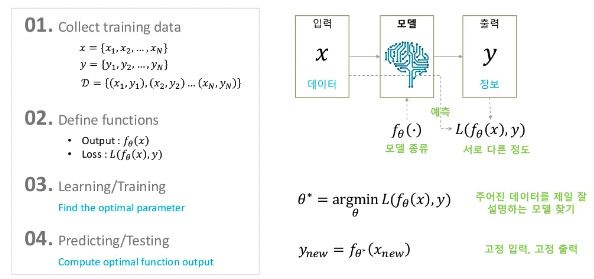
기존 머신러닝의 학습은 위의 이미지처럼 진행이 됩니다.

1. 입력과 라벨 데이터 쌍을 수집합니다.

2. 모델을 정의합니다. (SVM, Random Forest)

3. 입력 데이터를 가장 잘 설명할 수 있는 모델의 파라미터 $\theta$를 결정합니다.

4. 모델의 출력값과 라벨을 비교하기 위해 Loss function을 정합니다.

5. 파라미터를 조금씩 바꿔가며 최적의 파라미터를 찾습니다. 이 과정을 학습이라고 합니다.

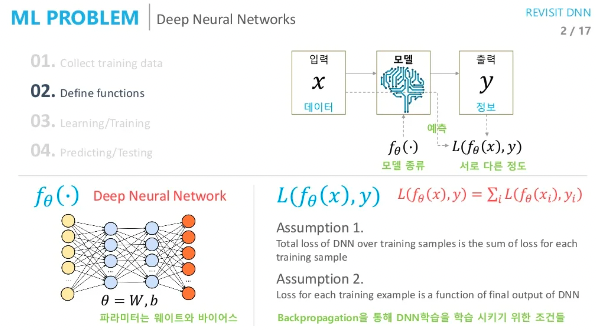
딥러닝의 학습은 아래와 같이 진행됩니다.

1. 데이터 수집은 동일합니다.

2. 모델을 어떤 뉴럴넷을 사용할지 정하게 됩니다. (CNN, RNN ..)

3. 학습할 파라미터는 주로 가중치(W), 편향(b)이 됩니다.

4. Loss function을 정의합니다. (Cross Entropy, MSE)

일반적으로 Loss function으로 사용되는것은 위의 2가지 정도입니다.
그 이유는 backpropagation algorithm을 적용하기 위함이고 이 알고리즘을 적용하기 위해서는 2가지 가정이 필요합니다.

• Train data 전체의 loss는 각각의 loss에 대한 합이다.

• 모델의 최종 출력값과 라벨에 대한 loss를 구한다. (중간의 값을 가져와 사용하는건 불가능)

gradient descent

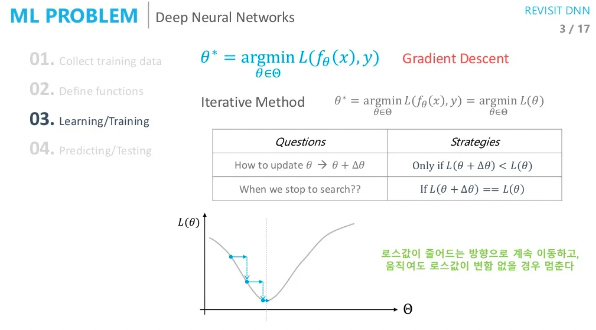
저는 위 이미지처럼 loss가 줄어드는 방향(기울기)으로 파라미터를 업데이트 한다고만 이해하고 있었습니다.
여기서 조금 더 자세히 어떠한 방식으로 파라미터를 업데이트하는지 알아보겠습니다.

그렇다면 현재 파라미터의 loss값보다 작은 loss값으로 파라미터를 업데이트 하는 방법은 무엇일까요?
그 답은 아래의 설명을 보시면 이해할 수 있습니다.

Taylor Expansion에서 1차 미분 term만 가지고 approximation하겠다는 것이 아이디어 입니다. 1차미분부터 2차미분 ... 많은 값을 사용하면 approximation값이 더욱 근사한 값을 같게 되지만 1차미분만 사용하면 현재 근방에서만 근사값을 추정할 수 있습니다. 이렇게 구한 근사식을 토대로 현재 loss function에 대한 파라미터의 기울기 값에 음의 값을 취하며 더 낮은 loss를 향해 업데이트할 수 있습니다.

모델을 학습하다 보면 lr(learning rate)값을 보신적이 있을텐데 이 위 사진에서 $\eta$로 표기 되어 있습니다. 대개 이 값은 매우 작게 설정합니다. 특히 이미지를 다루는 모델에서는 $10^{-7}$의 값을 사용 하기도 합니다. 그 이유는 approximation을 했을때 1차미분만 사용하기 때문에 샘플 포인트의 근처에서 근사값이 오차가 적기 때문입니다. 반대로 lr이 너무 크면 엉뚱한 방향으로 학습할 수 있다고 해석할 수 있습니다.

근본적으로 1epoch 마다 파마리터를 업데이트 하는게 맞습니다. 모든 train 데이터의 기울기를 minimum하는 것이 목표이기 때문이죠. 하지만 현실적으로 적용하기에 너무 많은 연산량이 필요로 하기 때문에 무작위로 배치를 뽑아 1step에 기울기들을 줄이는 방향으로 업데이트 하게 되며 SGD(Stochastic Gradient Descent)라고 부릅니다.

Backpropagation Algorithm

우리가 학습해야할 파라미터들은 가중치(weight)와 편향(bias)입니다.
많은 파라미터들에 대해 loss function을 미분을 해야하기 때문에 많은 연산량을 필요로 하게 됩니다.
이 불가능할 것 같던 계산을 가능하게 해준 것이 아래의 알고리즘 입니다.

1. 맨마지막 Layer부터 loss function과 activation function의 미분을 통해 error signal을 구합니다.

2. 각 Layer의 error signal은 이 전의 error singal과 activation function의 미분값을 통해 구합니다.

3. 이 방식이 앞단까지 진행되기 때문에 back-propagation이라는 용어를 사용합니다.

4. 각각의 layer별로 error signal이 구해졌으면 우리가 궁금한 파라미터(가중치, 편향)들의 기울기 값을 구해야 합니다. 편향의 기울기는 해당 layer의 error signal 자체이며 가중치의 기울기는 이 singal에 입력값으로 사용했던 값을 곱하면 가중치에 대한 기울기가 구해집니다.

두 가지 관점에서의 MSE & Cross Entropy

1. backpropagation이 잘 되도록 하는 관점(일반적으로 Cross Entropy가 좋다.)

2. ML의 관점 (continuous한 값에서는 MSE, discrete한 값에서는 Cross Entropy)

View-Point 1

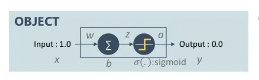
위 이미지에서 OBJECT의 영역의 형태처럼 입력값을 1.0로 했을 때 최종 출력값이 0.0이 되도록 학습 시키는 경우를 살펴보겠습니다.

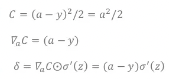
loss function을 MSE로 사용했을 때 backpropagation의 과정입니다.
현재는 layer가 한개로 설정했기 때문에 위 계산이 끝입니다.
이 layer에서의 가중치와 편향의 기울기를 구하는 것은 아래와 같습니다.

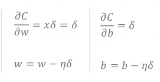
가중치는 해당 layer의 입력값인 x와 error sigal의 곱한 값이며 편향은 error signal 자체입니다. 현재 입력값은 1이고 출력값이 0이기 때문에 가중치와 편향이 같은 식으로 업데이트 됩니다.

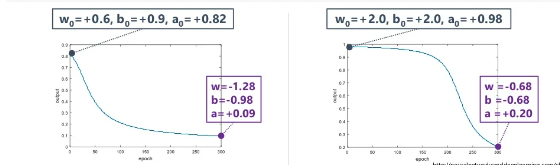
위 그래프처럼 가중치와 편향의 초기값만 다를 때, 같은 시점에서 학습을 중지시켰을 경우 왼쪽이 오른쪽보다 학습이 더 잘된 모델이라고 할 수 있습니다. 이처럼 초기값 설정이 결과에 큰 영향을 주게 되는 것을 알 수 있습니다. 그 이유는 무엇일까요?

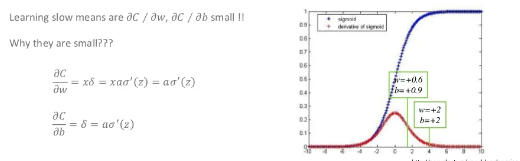
backpropagation 수식 자체에 activation function의 미분값이 들어가 있습니다.
오른쪽 그래프의 빨간선은 시그모이드 함수의 미분값을 나타냅니다. 이 값이 0에 가까울수록 가중치에 곱해지는 error signal이 작게 되므로 학습이 더딜 수 밖에 없습니다. 따라서 이 전의 이미지의 오른쪽 그래프는 초반에 더딘 학습을 진행하다가 어느정도 기울기 값이 생겼을때 출력값이 0에 가까워 지는 것을 확인하실 수 있습니다.
시그모이드의 기울기의 최대값은 약 0.4입니다. 현재는 한개의 layer를 가진 예를 들었지만 layer가 깊어질수록 이전의 기울기 값들이 계속 곱해지게 됩니다. 최대값이 0.4가 계속 곱해진다고 해도 이 값은 앞단으로 backpropagation될수록 0에 가까운 값이 될 수 밖에 없습니다. 이 문제를 gradient vanishing이라고 합니다. 이 문제를 해결하기 위해 activation function을 바꿔보자는 시도를 했으며 그 결과로 relu와 같은 함수를 사용하곤 합니다. 물론 무조건 좋다는 것은 아니지만 vanishing 문제에서 어느정도 보완이 되었다고 보실 수 있습니다.

그렇다면 loss function으로 Cross Entropy에 대해 알아보겠습니다.

MSE와 같은 방식으로 Cross Entropy를 미분한 값에 시그모이드값을 곱하면 절묘하게 activation function의 미분값이 사라지게 됩니다.

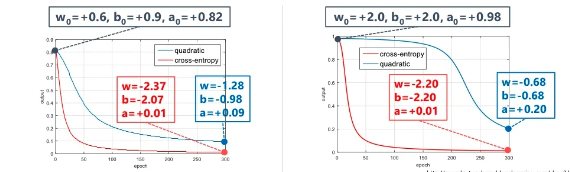
MSE에서는 학습이 더뎠던 경우와 달리 CE에서는 초기값의 영향을 크게 받지 않는 것을 볼 수 있습니다. 이처럼 backpropagation의 관점에서 봤을 때 Cross Entropy가 MSE보다 마지막 layer에서 업데이트를 더 잘할 수 있다고 볼 수 있기 때문에 학습이 잘된다고 볼 수 있습니다.

View-Point 2

같은 이야기지만 관점을 다르게 보면 다양하게 해석할 수 있습니다. 특히 지금부터 설명할 ML관점에서의 해석은 매우 중요합니다. $P(y|f_{\theta}(x))$는 네트워크의 출력값이 주어질 때 우리가 원하는 정답(y)가 나올 확률이 높길 원하다는 겁니다. 어떤 확률분포가 있을때 likelihood값이 최대화가 되는것을 원하기 때문에 우리는 확률분포를 정하고 들어가야 합니다. 예를들어 "가우시안 분포를 따를것이다. 베르누이 분포를 따를 것이다."를 정의해야 합니다.

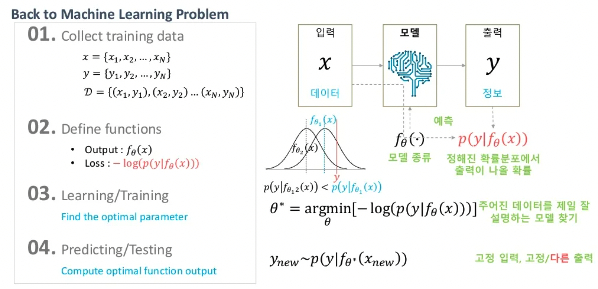
이런 관점으로 다가가면 네트워크의 출력값은 확률분포를 정의하기 위한 파라미터입니다. 예를들어 위의 이미지처럼 가우시안분포를 따른다고 해봅시다. 해당 출력값이 평균값이라고 해석을 할 때 y값이 나올 확률이 최대가 되도록 하는 겁니다.

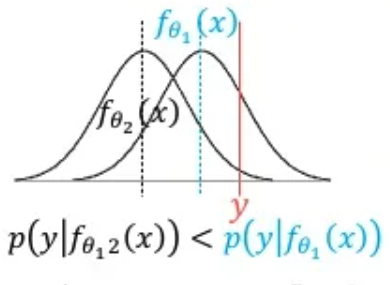
y값은 실제 데이터에 있는 값이므로 정해진 어떠한 값입니다.
현재 $\theta_{2}$일 때 출력값은 평균이라고 해석할 거라고 가정했습니다. 이때의 likelihood값은 매우 낮은 것을 확인할 수 있습니다. 학습이 진행되며 $\theta_{1}$로 바뀌었다고 생각해봅시다. 이 시점의 likelihood는 $\theta_{2}$일때 보다 커진 것을 볼 수 있습니다. 직관적으로 출력값(평균)이 y값과 같을 때 가장 높은 likelihood를 갖는 것을 알 수 있습니다.
결과적으로 네트워크의 출력값이랑 정답이랑 가깝기를 원한다는 것과 같습니다.

loss function은 확률이기 때문에 음의 값을 가지고 backpropagation하기 위해 log를 사용하게 됩니다.

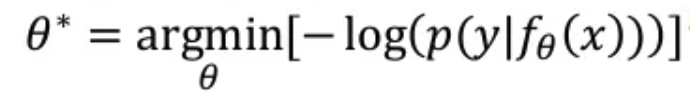
negative log likelihood값을 찾게 되면 가장 높은 확률은 찾는 것과 마찬가지 입니다.
여기서 중요한 관점의 차이는 정답을 찾았다는 것과 확률분포의 파라미터를 찾았다는 점입니다.
정답을 찾았다는 것은 고정된 입력에 고정된 출력을 보여주겠지만 확률분포를 찾았다는 것은 새로운 입력에 대해 다양한 샘플링이 가능하게 되며 적절한 성향을 가진 여러 데이터를 볼 수 있다는 점입니다.

가우시안 분포 모델이라고 가정했을 때 확률분포를 풀어보면 결국 MSE를 사용하는 것과 같게되고 베르누이 분포 모델이라고 가정했을 때는 Cross Entropy를 사용하는 것과 같다.

정리를 해보자면 아래와 같습니다.

backpropagation의 관점에서 봤을 때 Cross Entropy를 사용하는게 유리하고 그 이유는 최종단에서 activation function의 미분값 만큼 더 학습되기 때문입니다.
ML의 관점에서 봤을 때 MSE를 사용한다는 것은 출력값이 continuous value이며 가우시안 분포에 가까울 것이라는 가정이며 Cross Entropy를 사용한다는 것은 discrete value이며 베르누이 분포에 가까울 것이라는 결론을 낼 수 있습니다.