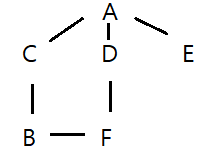
그래프 ?
지금까지 봐온 트리구조의 특성은 루트가 있고 아래로 자식노드들이 있으며, 이 부모노드와 자식노드를 이어주는 edge가 존재하며 방향은 부모노드에서 자식노드로 흘렀다. 또한 들어오는 곳은 한개이며 나가는 곳은 두개(혹은 여러개)인 구조였다.
그래프(Graph)는 위와 같은 구성이 아닌 방향도,들어오는 곳의 개수도, 자식노드가 없기도 하고 그 밖의 다양한 구조를 띄는것이 그래프이다. 트리는 그래프의 한 형태로 볼 수 있다. ( 여러가지 조건이 있는 방향 그래프 )
그래프 구조는 G = ( V, E )로 나타낼 수 있다.
G : Graph
V : Vertex set ( 트리에선 Node라고 했음 )
E : Edge set
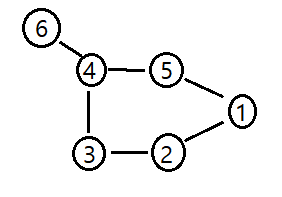
위와 같은 구조가 있을 때
V = { 1, 2, 3, 4, 5, 6 }
E = { (1,2) , (2,3) , (1,5) , (3,4), (6,4), (2,1) ... }
|V| = n ( V 집합의 크기 )
|E| = m ( E 집합의 크기 )
로 표현할 수 있다.
-
그래프 구조는 위에서 아래로의 계층형 구조가 아니기 때문에 그래프 구조의 degree는 인접하게 이어진 edge의 수이며 그래프의 degree는 가장 큰 degree의 값이다. ( 4의 degree : 3 )
-
adjacency하다라는 말은 노드 3과 노드 2는 adjacency하다.
-
incident하다 E(2,3)은 노드 2와 3에 incident하다.
-
경로(path) : 1에서 3으로 가는 경로 ?
- 1 -> 2 -> 3
- 1 -> 5 -> 4 -> 3
- 한번 갔던 노드를 다시 가는 것은 경로에 포함시키지 않는다.
-
Cycle 구조 : 처음과 끝이 같은 경우
- 1 -> 2 -> 3 -> 1
- 위와 같이 처음과 끝이 같은 경우이며, 그래프 내에 존재할 수도 존재하지 않을 수도 있다.
- cycle이 없는 그래프 ? --------> Tree 구조 ( 자식노드에서 부모노드로 이어지지 않음 )
- cycle 내의 어떤 노드에서 어떤 노드로의 경로는 최소 2개 이상이며, cycle이 없으면 경로는 한가지 밖에 존재하지 않는다.
그래프방향
- Undirected graph
- edge의 방향이 없는 그래프 ( 양방향 그래프 )

- Directed graph
- 방향이 있는 그래프로 1에서 5로는 바로 이동할 수 없다.
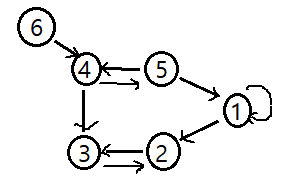
- weight graph
- 그래프의 edge에 가중치가 존재하는 그래프
그래프표현
그래프를 표현한다는 것은 인접성 ( adjacency )를 나타내는 것이다.
- 인접 행렬 ( adjacency matrix , n x n 행렬 , O(N^2) )

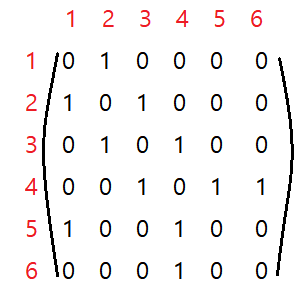
단점 : 정보의 표현보다 낭비되는 메모리 ( 0인 개수 ) 가 너무 많아 효율이 떨어진다.
- 인접 리스트 ( adjacency list , O(n+m) )
- 여기서의 리스트는 linked list를 의미한다.
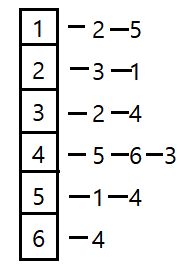
순서 상관 없이 linked list로 표현하는 방법이다.
인접 리스트 방법을 사용할 때 노드의 개수는 edge의 개수의 2배 만큼 생긴다. ( undirected 경우 양방향이기 때문이다. )
그래프순회
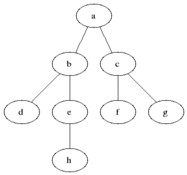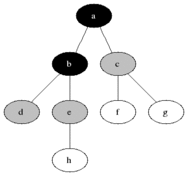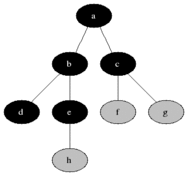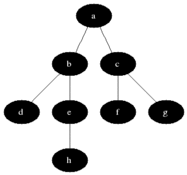
DFS ( Depth - First Search )
Binary tree를 순회할때 사용했던 in,pre,postorder 들이 DFS에 속한다.
하나의 자식노드를 방문하면 그 해당노드의 자식노드를 끝까지 파고들어 탐색 후 , 다음 분기(brach)에 있는 곳으로 이동하는 순회방법이다.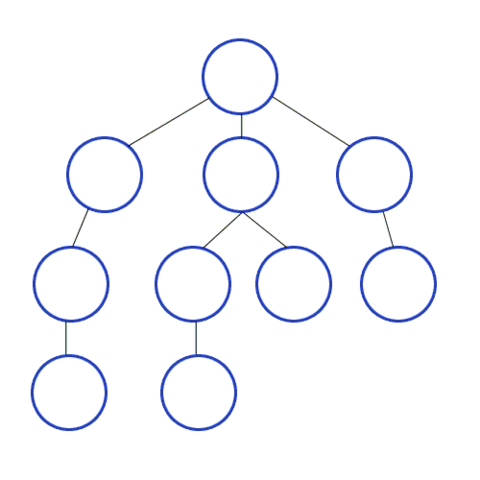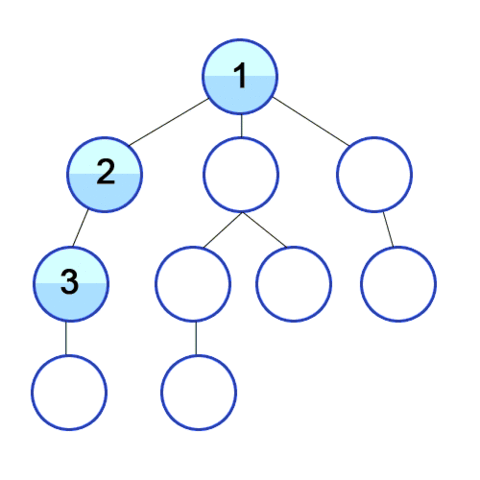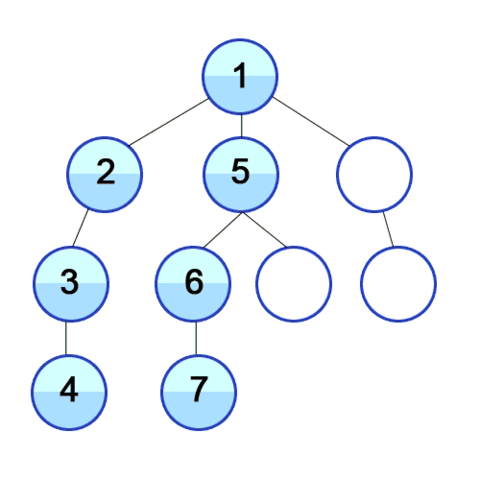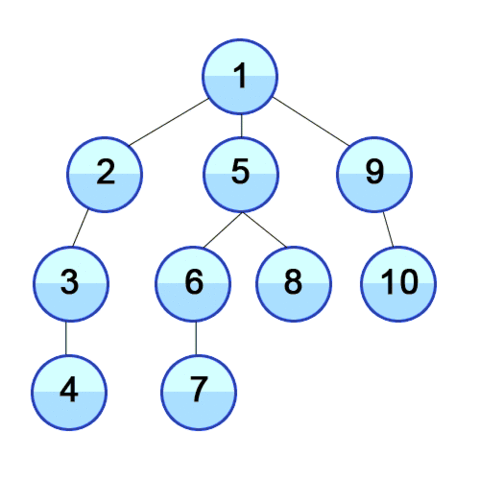
출처: 위키디피아
BFS ( Breadth - First Search )
레벨 단위로 순회하는 것이 BFS이다.
출처: 위키디피아
DFS,BFS -Python 구현
class Graph:
def __init__(self):
self.graph = {}
def addInfo(self,start,edges):
self.graph[start] = edges
def addEdge(self,start,edge):
self.graph[start].append(edge)
def addVertex(self,Vertex):
self.graph[Vertex] = []
## BFS는 Queue구조로 구현가능하다.
def BFS(self,start):
Q = [start]
visited = [start]
while Q:
cur_V = Q.pop(0)
for next in self.graph[cur_V]:
if next not in visited:
Q.append(next)
visited.append(next)
return visited
## DFS는 스택과 재귀로 구현가능하다.
def DFS(self,start):
S = [start]
visited = []
while S:
cur_V = S.pop()
if cur_V not in visited:
visited.append(cur_V)
S.extend(self.graph[cur_V][::-1])
return visited
def DFS_recursive(self,start,visited=[]):
visited.append(start)
for next in self.graph[start]:
if next not in visited:
self.DFS_recursive(next,visited)
return visited
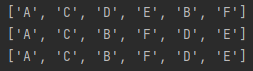
if __name__=="__main__":
G = Graph()
G.addInfo('A',['C','D','E'])
G.addInfo('B',['F','C'])
G.addInfo('C',['A','B'])
G.addInfo('D',['A','F'])
G.addInfo('E',['A'])
G.addInfo('F',['D','B'])
print(G.BFS('A'))
print(G.DFS('A'))
print(G.DFS_recursive('A'))