평균으로의 회귀

어떤 변수를 지속적으로 측정할 때, 이상치가 관찰되면 그 다음에는 평균에 가까운 값이 측정되는 경향성

• [데이터 과학을 위한 통계학]

따라서 평균으로의 회귀에 기반하여, 이상치가 측정되더라도 그것을 너무 확대해석하거나 맹신하지 않는 것이 필요하다.

🚨 선형 회귀나 로지스틱 회귀와 같은 회귀와는 다르다. 그냥 통계적 법칙이다.
선형 회귀 등은 통계분석방법에 속한다.

평균으로의 회귀 살펴보기

출처 : KHUDA 박선우 선생님 <3

데이터 살펴보기

#scatter plot으로 먼저 확인을 해보자
import matplotlib.pyplot as plt
import seaborn as sns
fig = plt.figure()

# 실습:  scatterplot을 그려보자, x는 Father, y는 Son이다
x = data['Father']
y = data['Son']
sns.scatterplot(x, y)######)

# line where the son's and father's heights are equal,
plt.axline(xy1 = (150,150), #intercept
          slope = 1, #slope
          linewidth = 2,
          color='green')

# x와 y 같게 한다
plt.axis('equal')
plt.show()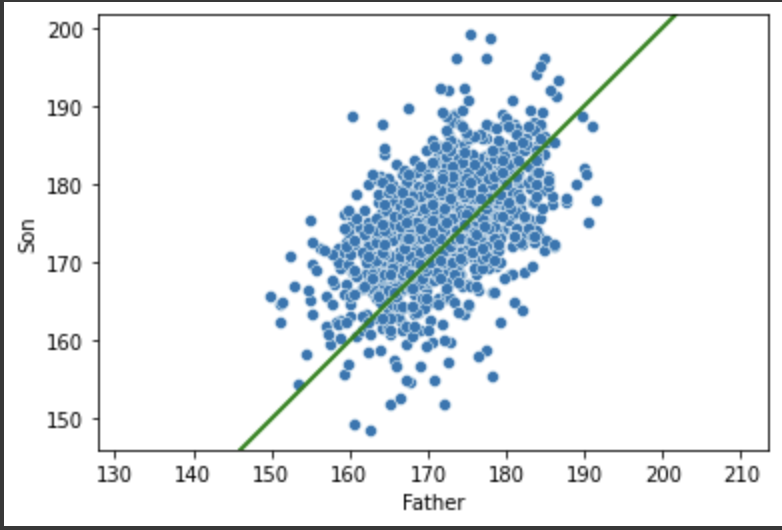

#Regression line 

fig = plt.figure()

#실습: Regplot을 그려보자 color는 black이다
sns.regplot(x=x, y=y, color='black')#####)

plt.axline(xy1 = (150,150),
           slope=1,
           linewidth=2,
           color='green')

plt.axis('equal')
plt.show()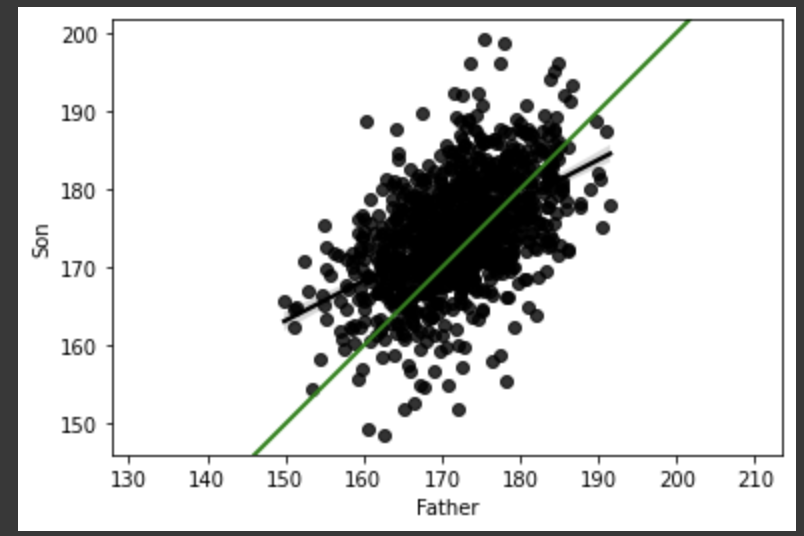

• 초록색 직선의 기울기는 1이다 (y=x)
• 검은색 직선은 회귀직선이다
• 초록색 직선과 검은색 직선의 교차점 기준 왼쪽을 보면, 아버지의 키가 아무리 작아도, 그 아들은 아버지보다 대략 크다
• 반대로 오른쪽을 보면 아버지의 키가 아무리 커도 그 아들은 대략 작다

이렇게 아버지/아들의 신장 그래프로 봤을 때, 아버지의 키가 평균보다 많이 크거나 작아도 그 아들의 키는 대략 평균으로 회귀한다는 사실을 알 수 있다.