통계
1.[통계] 데이터와 표본분포
표본 (sample) : 더 큰 데이터 집합으로부터 얻은 부분집합모집단 (population) : 어떤 데이터 집합을 구성하는 전체 집합임의표본추출 (Random sampling) : 무작위로 표본을 추출하는 것단순임의표본(simple random sample) : 층
2.[통계] 표본평균과 모평균 (+표준오차, 자유도 )
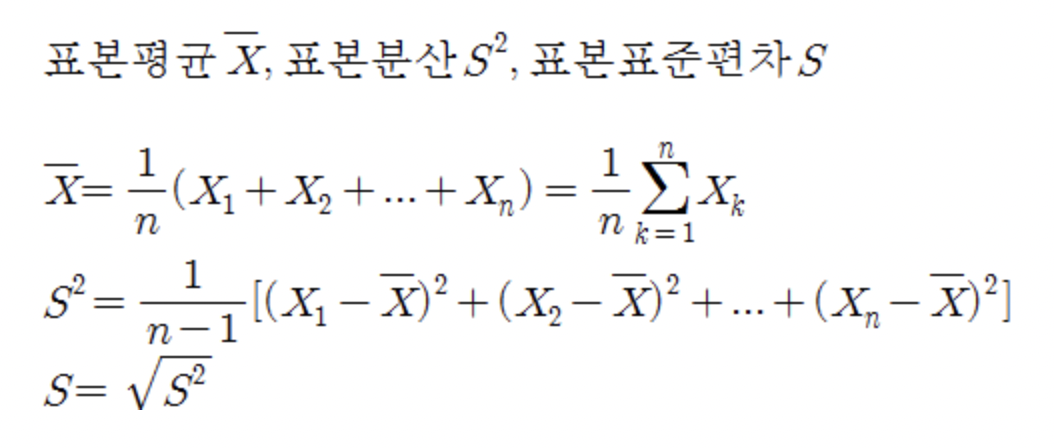
표본평균이란, 모집단에서 표본추출법을 이용해 추출한 표본의 평균이다.헷갈리면 안 되는 부분이, 모집단의 단일 표본 하나의 평균이다 !! 모든 표본의 평균값이 아님.아래 사진은 표본평균과 표본분산, 표본표준편차에 대한 공식이다.출처 : https://blog.
3.[통계] 표본추출법
📊 모집단 (population) : 어떤 데이터 집합을 구성하는 전체 집합 📊 표본 (sample) : 모집단의 특성을 파악하기 위해서 모집단으로부터 추출한 모집단의 일부 집단모집단의 크기는 대부분 늘 너무 크고 방대하고, 모든 데이터를 모으기도 힘들기에 그의
4.[통계] 선택편향

선택 편향(영어: selection bias) 또는 선택적 보고(영어: selective reporting)는 표본을 사전 또는 사후 선택함에 따라 통계 분석을 왜곡하는 오류출처 : 위키백과추출한 데이터를 가지고, 혹은 잘못된 표본을 추출하여 편향된 Output을 내게
5.[통계] 평균으로의 회귀
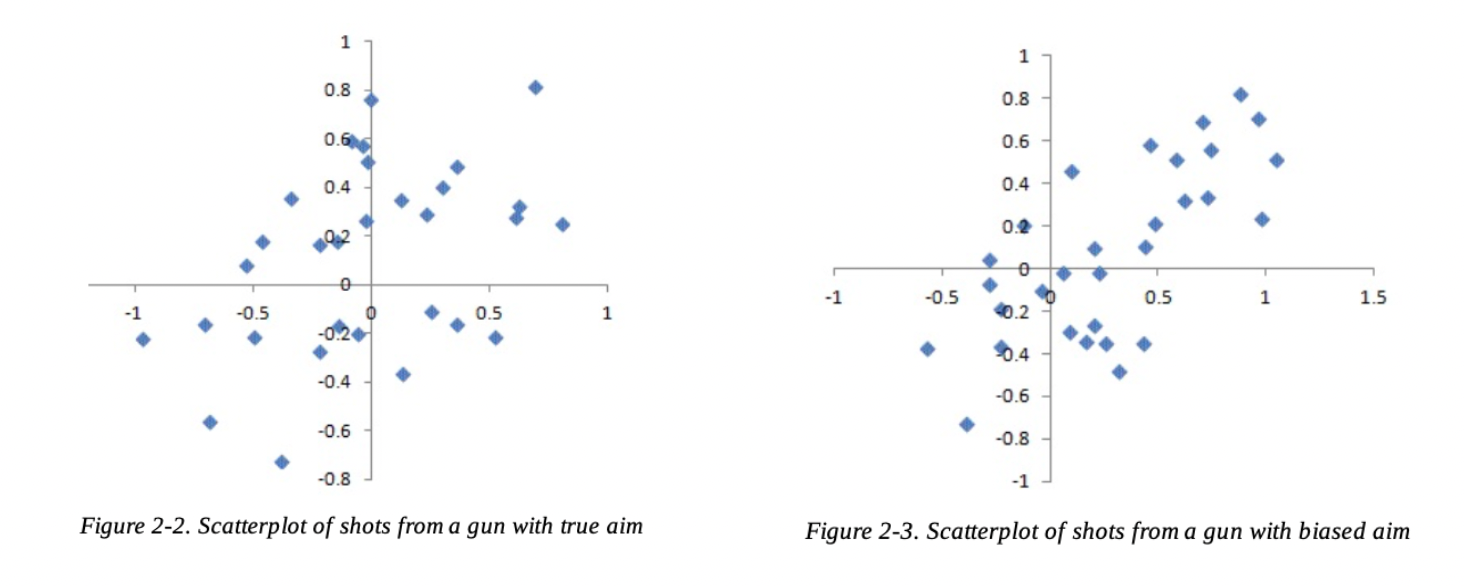
어떤 변수를 지속적으로 측정할 때, 이상치가 관찰되면 그 다음에는 평균에 가까운 값이 측정되는 경향성데이터 과학을 위한 통계학따라서 평균으로의 회귀에 기반하여, 이상치가 측정되더라도 그것을 너무 확대해석하거나 맹신하지 않는 것이 필요하다.🚨 선형 회귀나 로지스틱 회귀
6.[통계] 중심극한정리
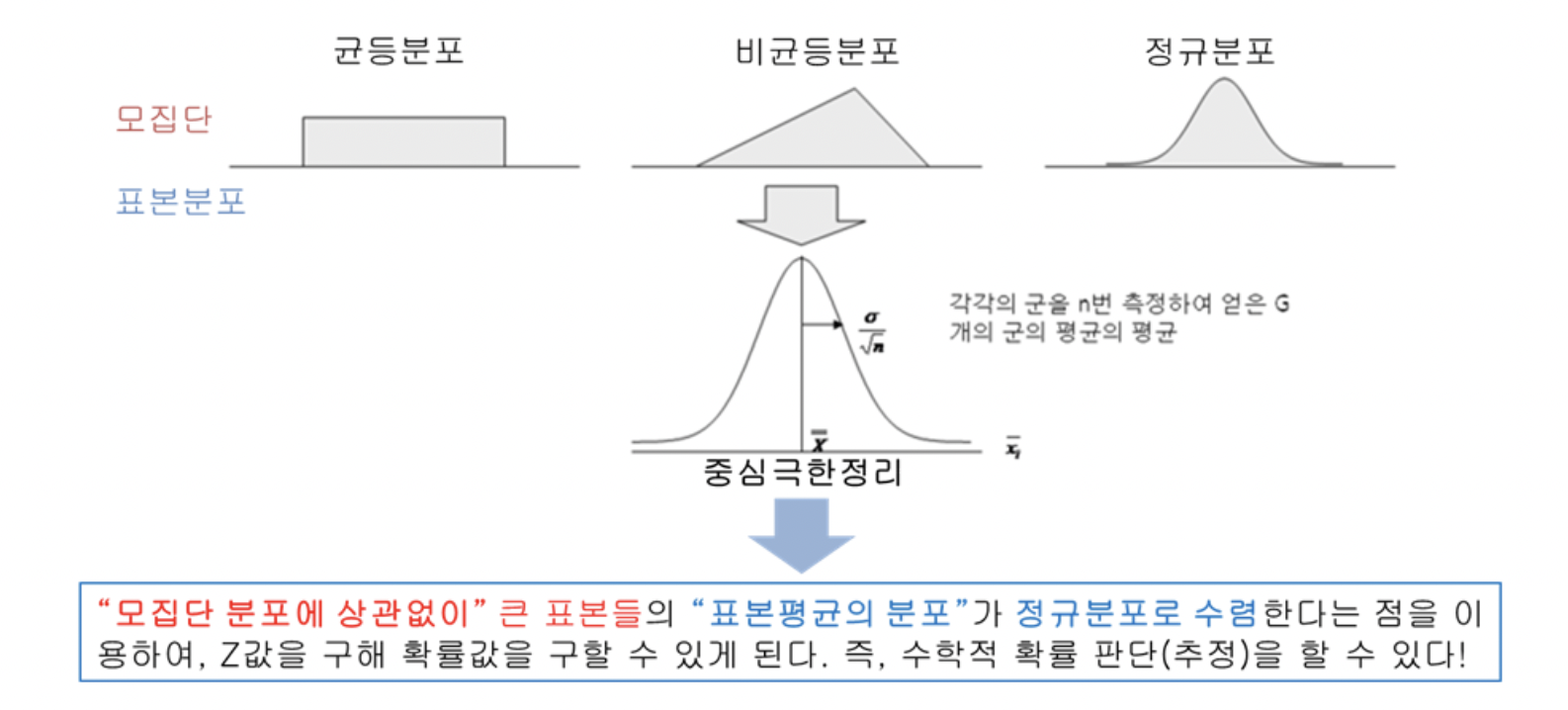
중심극한정리 (Central Limit Theorem, CLT)는 동일한 확률분포를 가진 독립 확률 변수 $n$개 평균의 분포는 $n$이 커질수록 평균이 $\\mu$이고 표준편차가 $\\frac{s}{\\sqrt{n}}$인 정규분포에 가까워진다는 정리이다.중심극한정리는
7.[통계] 부트스트랩
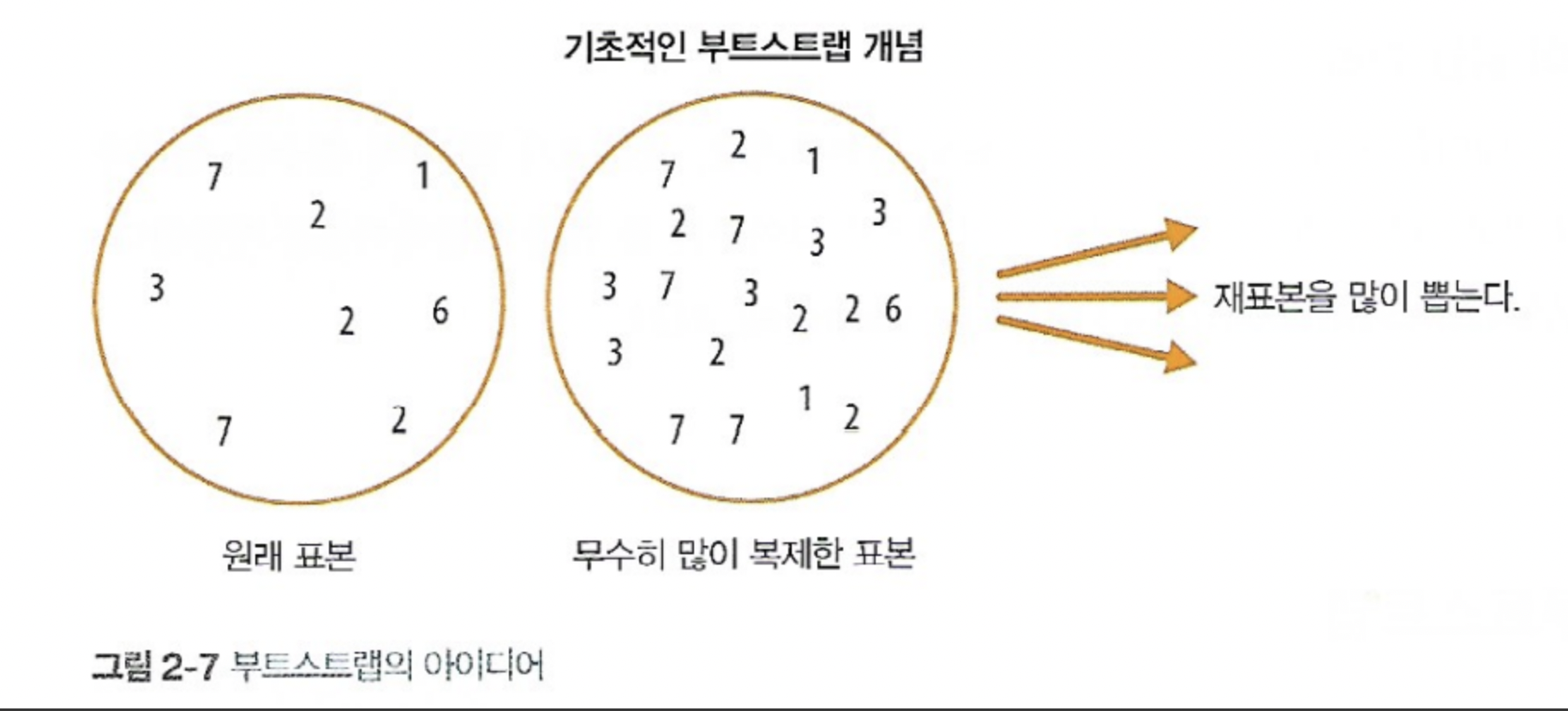
가설 검증(test)을 하거나 메트릭(metric)을 계산하기 전에 임의복원추출을 적용하는 방법을 일컫는다. 딱 하나의 통계치를 얻고 싶으면 전체의 평균을 구하면 된다. 그런데 만약 평균의 신뢰구간을 구하고 싶은데, 데이터를 수집했던 확률변수의 정확한 분포를 모르는 경
8.[통계] 신뢰구간
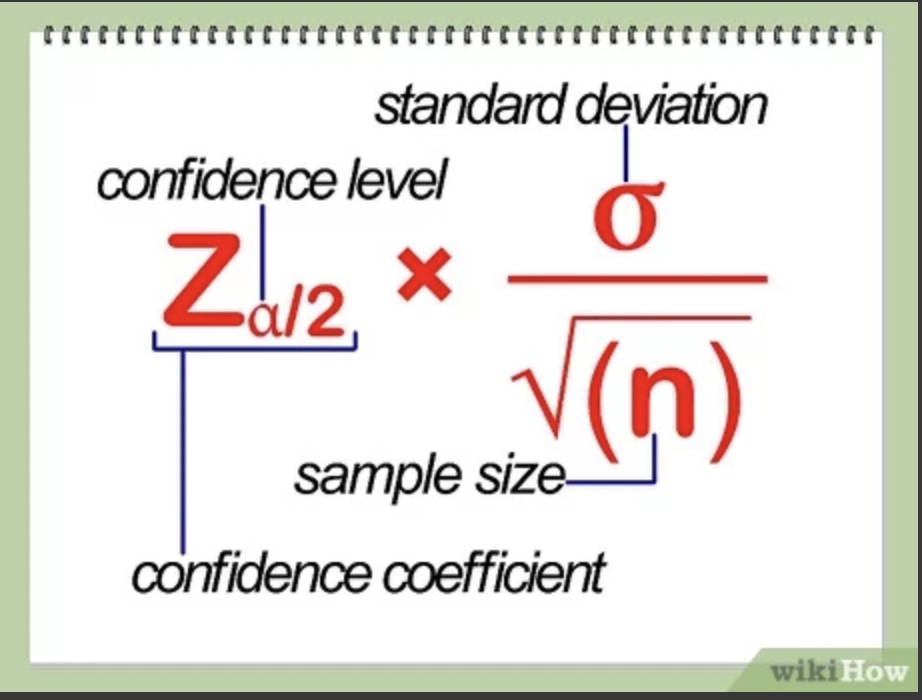
출처 : wikiHow신뢰구간은 $X\\pm Z\_{\\frac{\\alpha}{2}}\\frac{\\sigma}{\\sqrt{n}}$으로 계산된다.📊 신뢰구간은 모수가 실제로 포함될 것이라고 예상되는 범위이다.말이 조금 어려운데, 우리가 약속을 잡을 때 "한 10~
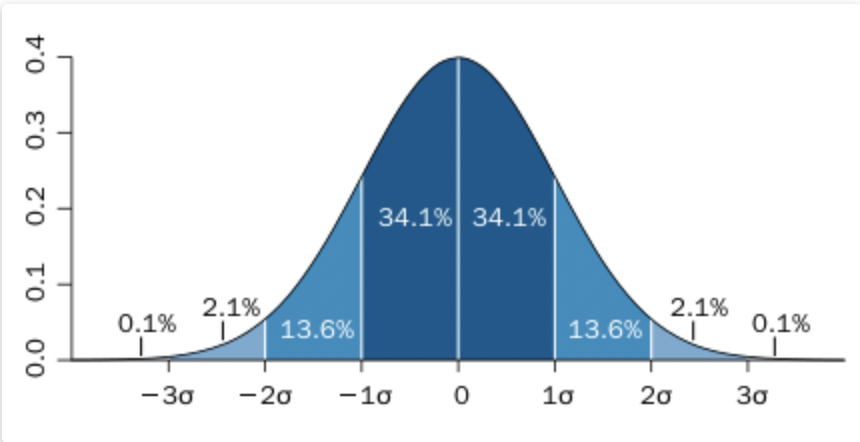
9.[통계] 정규분포
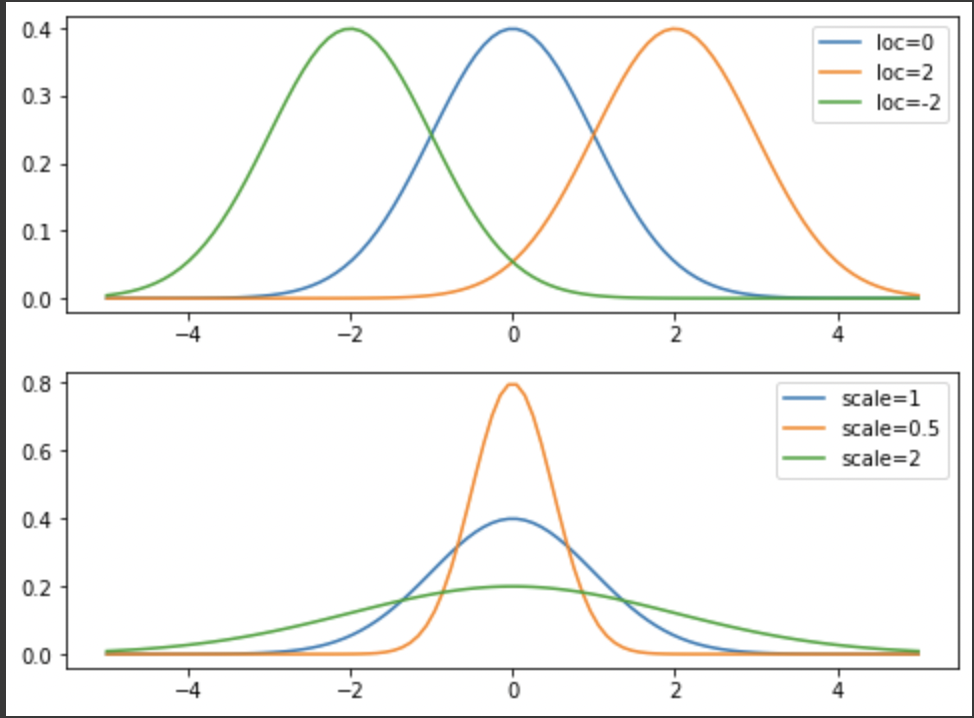
이번에 다룰 친구는 아주아주 유명한 분포인 정규분포!
10.[통계] 긴꼬리 분포 (Long-Tailed Distribution)

📚 긴꼬리 분포 전 포스팅에서 다뤘던 정규분포가 유명하고 대표적인 분포인 것은 맞지만, 원시 데이터는 정규분포를 잘 따르지 않는다. 어떤 데이터에서는 저빈도의 극단값이 나타날 수도 있는데, 이 경우 🦎그래프의 꼬리가 한 쪽으로 길어지게 되므로 긴꼬리 분포와 같은
11.[통계] 카이제곱분포 (Chi-Squared Distribution)

출처 : https://blog.naver.com/mykepzzang/220852102307확률변수 $X$가 카이제곱분포를 따르면 $\\chi^2(v)$로 표현한다고 한다.확률밀도함수를 그래프로 그려보면 다음과 같다. 그래프는 자유도 $df$에 따라 달라진다.
12.[통계] 스튜던트의 t분포
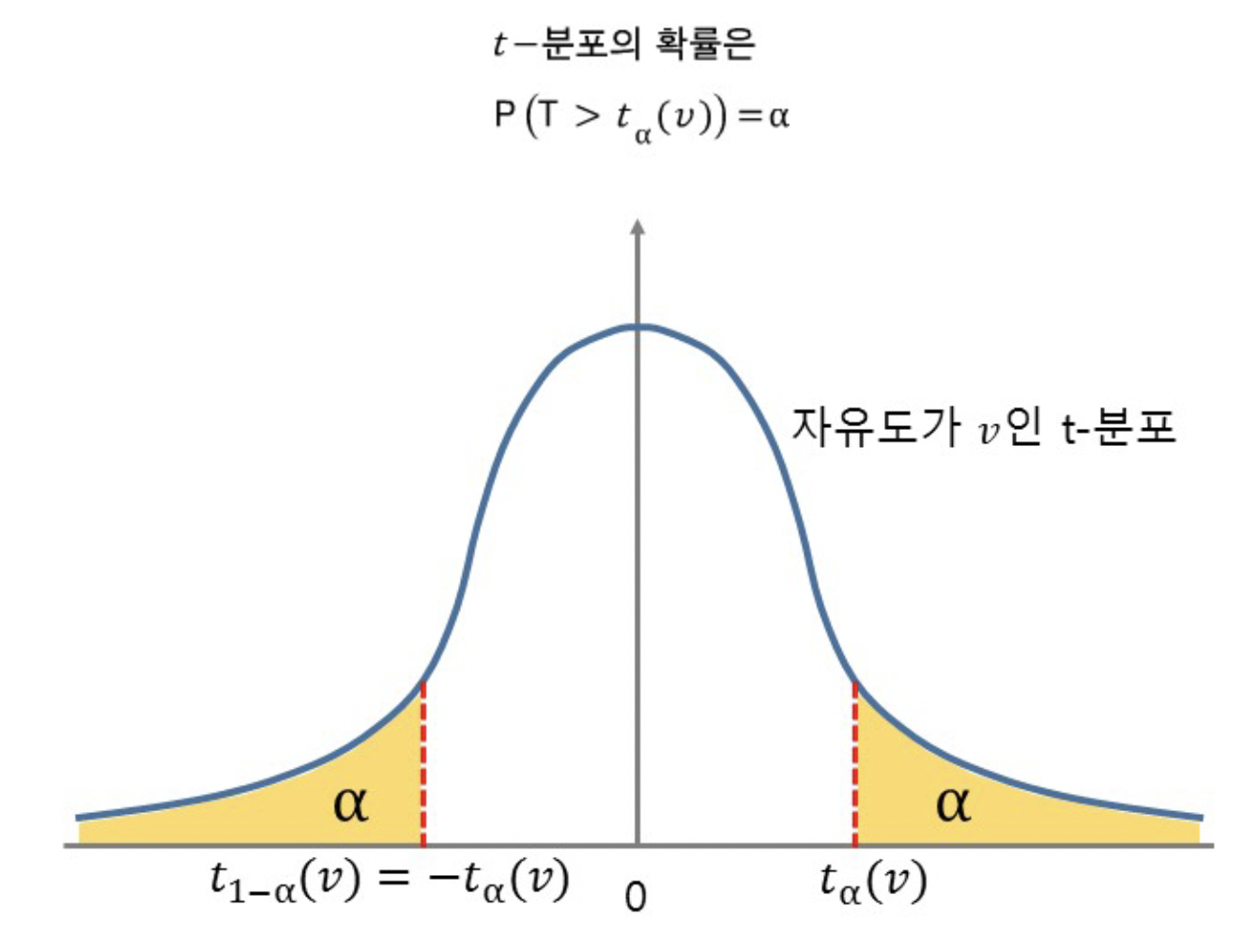
📚 t 분포란? >💡 $t$ 분포는 정규분포와 생김새가 비슷하지만, 꼬리가 더 두껍고 길다는 차이점이 있다. 💡 표본평균을 이용해서 정규분포의 평균을 해석할 때 많이 사용한다. 💡 가설검정이나 회귀분석에도 많이 쓰인다고 한다. 모집단이 정규분포를 따를 때, 표
13.[통계] 이항분포
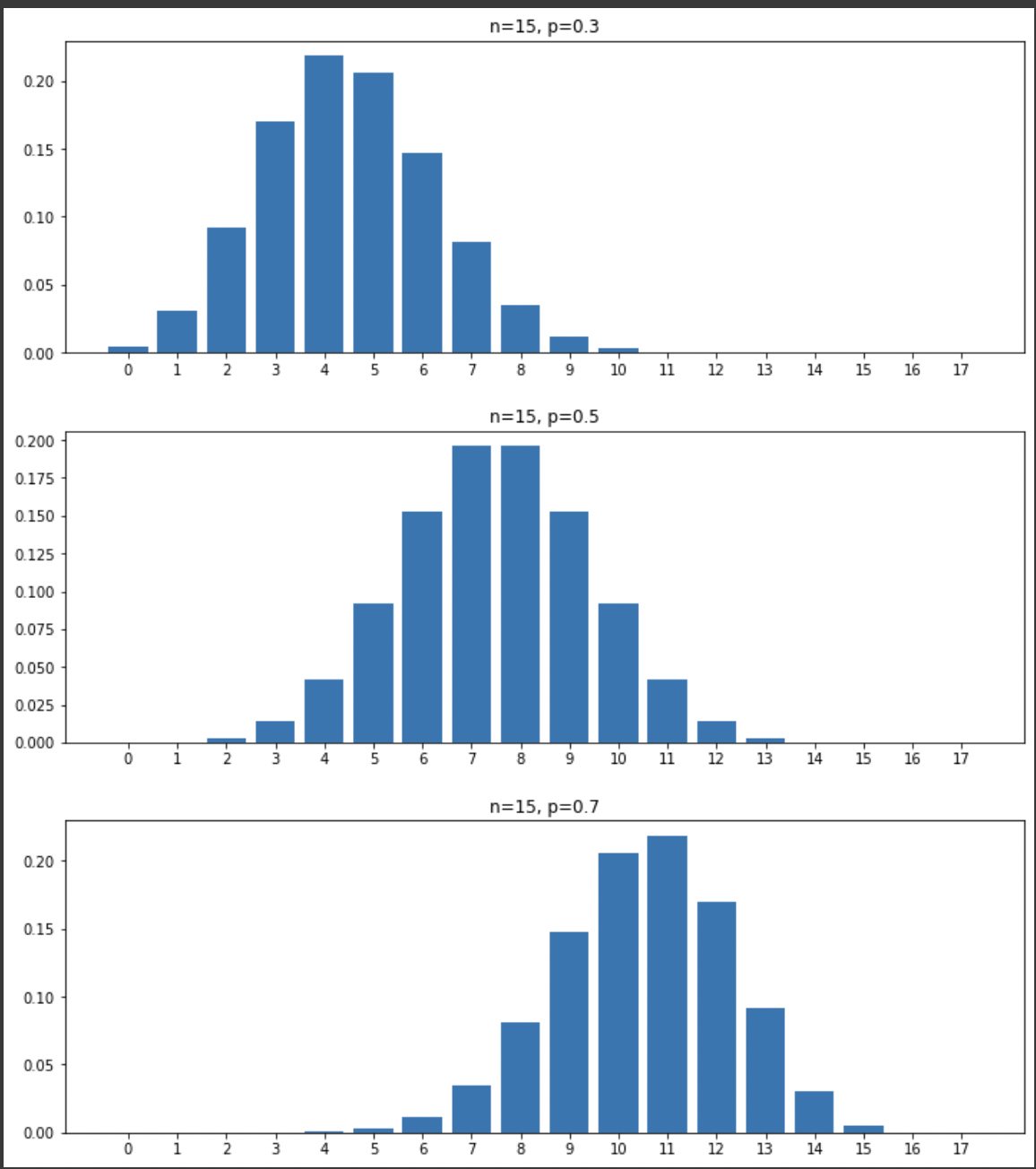
이항분포란 각 시행마다 성공 확률이 정해져 있을 때, 주어진 시행 횟수에서 성공한 횟수의 도수분포를 뜻한다.가장 유명한 예시로 동전 던지기가 있는데, 각각의 회차마다 성공 : 실패 확률이 5:5로 정해져 있기 때문.이 때 $n$번의 회차에서 $k$번 성공할 확률을 이항
14.[통계] F 분포 (F Distribution)

F분포의 확률변수는 두 개의 독립인 카이제곱분포 확률변수의 비로 정의한다.! 카이제곱분포가 한 집단의 분산을 다룬다면, F분포는 두 집단의 분산을 다룬다.이 과정에는 나눗셈이 쓰인다.확률밀도함수는 다음과 같이 흉악하게 생겼다.다만 여느 복잡한 확률변수처럼, 우리가 이를
15.[통계] 푸아송 분포
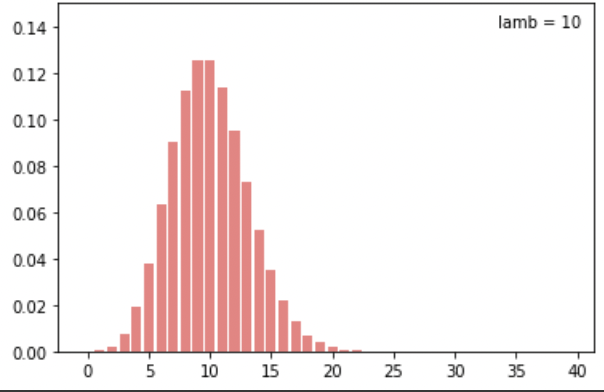
푸아송 분포의 확률밀도함수는 다음과 같이 정의된다.$$X \\sim P_X(x)=\\frac{\\lambda^xe^{-\\lambda}}{x!} ,\\; x=0,\\; 1,\\; 2,\\; ...\\$$이는 주로 일정한 시간 혹은 공간 단위에서 평균적인 사건의 수에 대
16.[통계] 지수분포 (exponential distribution)
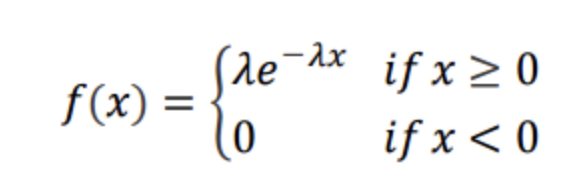
지수분포의 PDF는 위와 같이 정의된다.지수분포는 사건과 사건 사이의 시간을 나타내는 확률분포라고 한다.그래서인지 포아송에서의 사건 파라미터와 동일한 람다 $\\lambda$ 파라미터가 존재한다.$$EX=\\frac{1}{\\lambda}$$$$VarX = \\frac
17.[통계] 베이불 분포
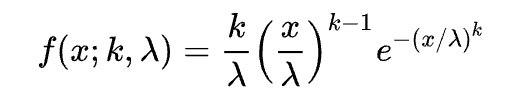
베이불 분포의 PDF는 위 사진과 같이 정의된다.베이불 분포는 시간에 따른 사건의 발생 비율이 변화할 때 사용된다.사건의 발생 비율이 변화하지 않는다면 그냥 지수분포와 동일하다.부품의 수명 추정 분석,날씨예보 등에 사용된다고.
18.[통계] QQ plot
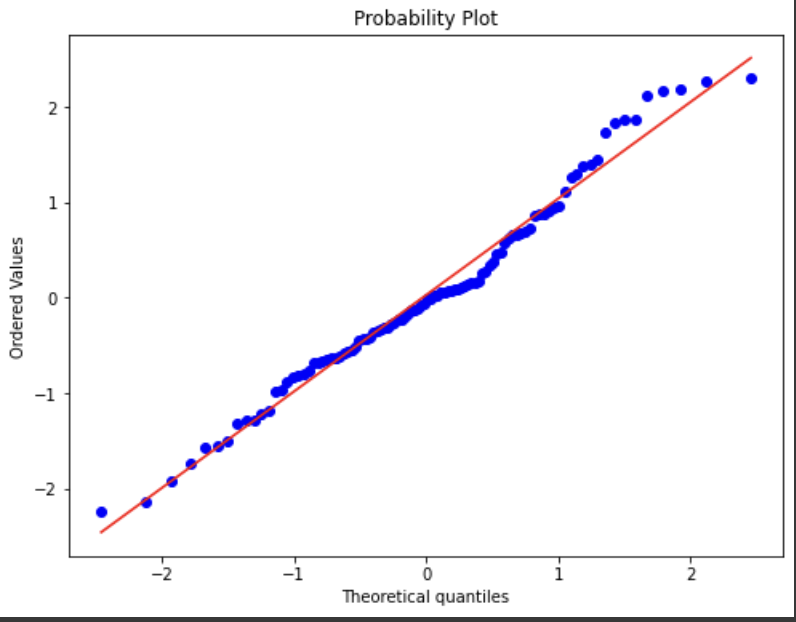
QQ 플롯의 QQ는 Quantile-Quantile인데, 이는 '분위'를 뜻한다.수집된 데이터를 표준정규분포의 분위수와 비교하여 그리는 그래프이다.통계 추론은 대부분이 모집단이 정규분포를 따른다는 것을 전제로 하는데, 이 QQ 플롯은 정규분포 가정을 하는 데 용이하다.
19.[통계] A/B 검정

💡 집단을 실험군과 대조군, 두 그룹으로 나누어 진행하는 실험.💡 한 쪽은 기존의 처리 방법 혹은 무처리, 다른 쪽은 새로운 처리를 한다.💡 가설은 대조군보다 실험군이 더 낫다가 된다.💡 주로 검정통계량을 이용해서 두 집단을 비교한다.
20.[통계] 가설검정

관찰된 효과가 우연에 의한 것인지, 통계적으로 유의미한 차이가 있는지 검정하는 과정.'차이는 우연 때문이다' 라는 가설.따라서 귀무가설이 틀렸다는 것을 입증해서 , 그룹 간 차이가 우연에 의해 발생한 것이 아니라는 것을 밝히는 것을 주로 목적으로 삼는다.💡 이를 검정
21.[통계] 재표본추출 (부트스트랩과 순열검정)
표본을 반복적으로 추출하여, 무작위 변동성을 알아보는 것.머신러닝 모델의 정확성을 평가하고 향상시키기 위해 적용 가능. \- 부트스트랩 데이터 집합을 기반으로 각 표본 당 의사결정트리 예측의 평균을 구함으로써 평균 예측값을 구할 수 있다(배깅)어떤 분포에서 생성된 지
22.[통계] 통계적 유의성과 p값
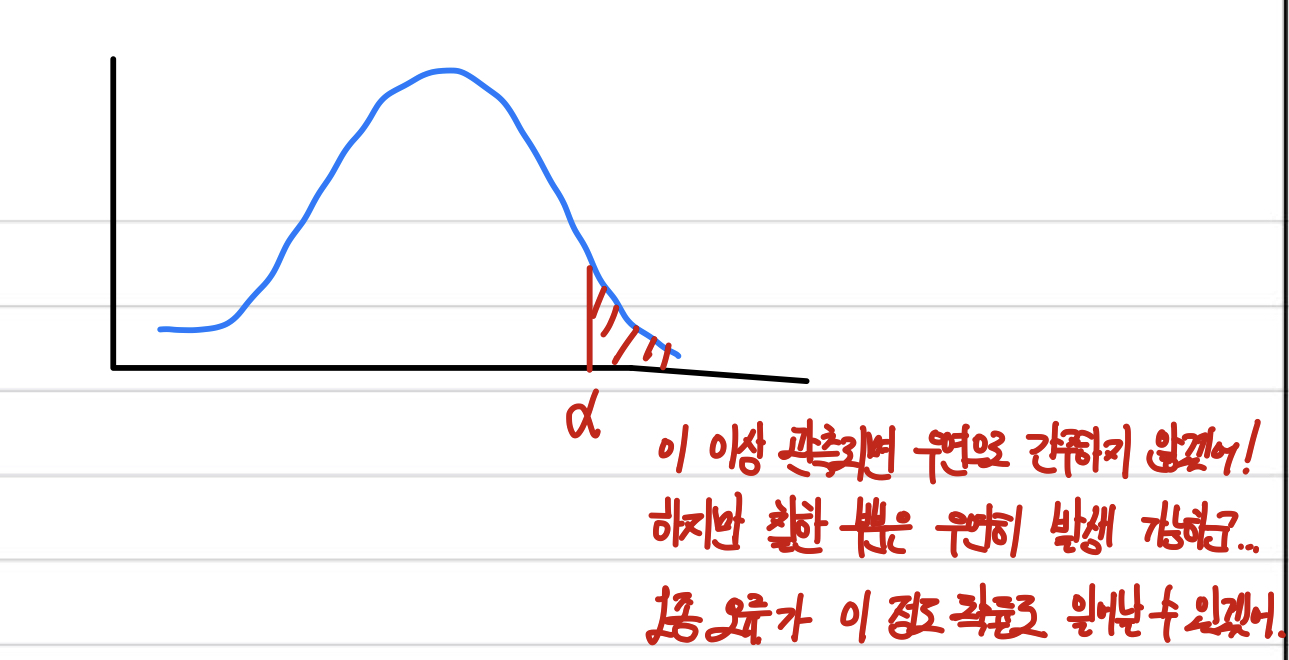
통계학자의 실험 결과가 우연히 일어난 것인지, 혹은 우연히 일어날 수 없는 극단적인 것인지를 판단하는 방법이다.결과가 우연히 벌어질 수 있는 변동성의 바깥에 존재한다면 이것을 통계적으로 유의하다 라고 한다.😵💫 귀무가설이 참이지만 귀무가설을 기각하는 경우🧐 귀무
23.[통계] t검정
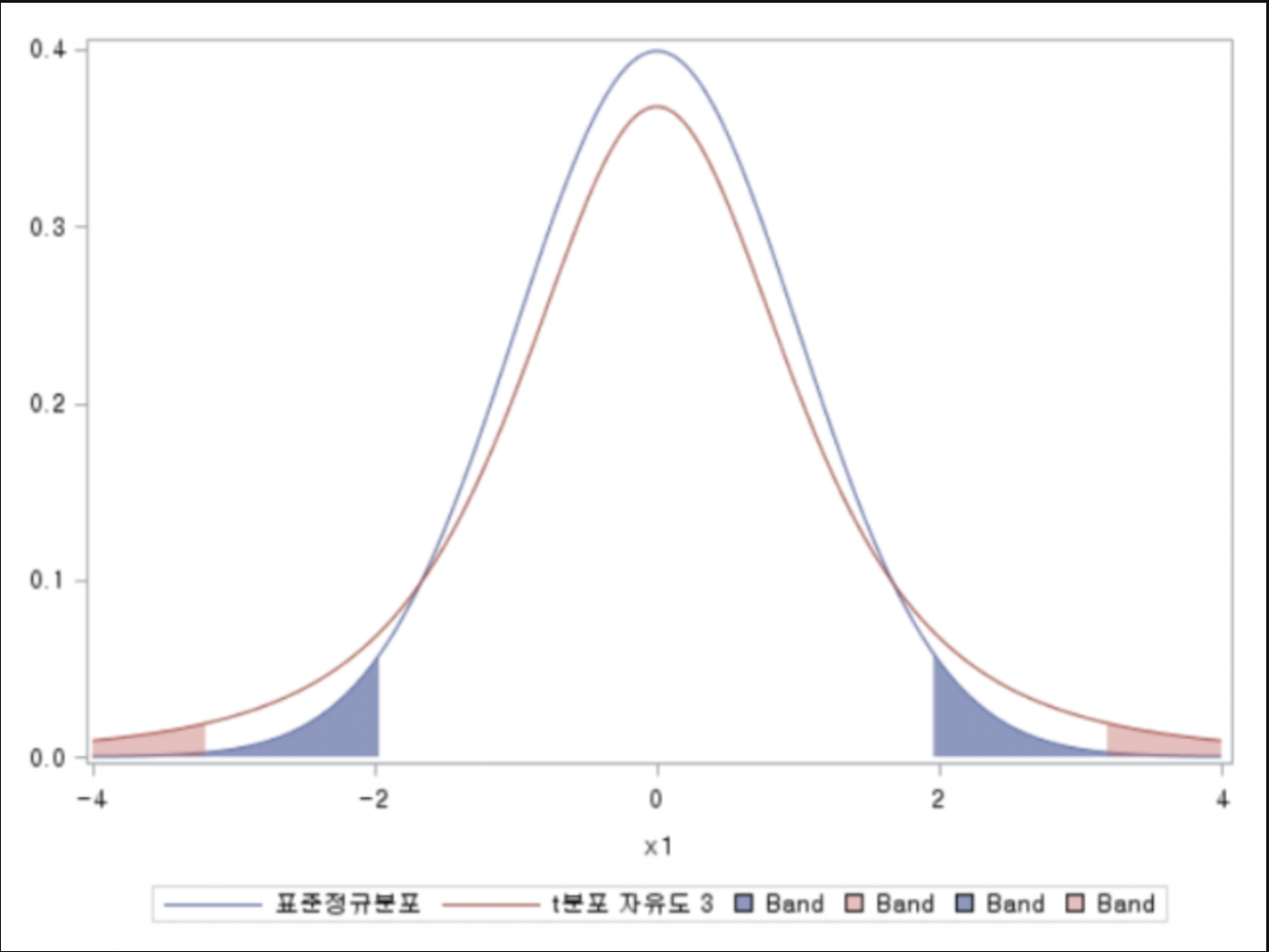
이전 포스팅에 정리해둔 게 있다.\[통계] t분포간단하게 다시 복기해보자.모분산을 이용하지 않고 표본평균의 분포를 가늠할 수 있도록 하는 분포다.표본평균의 분포는 다음과 같은 식을 따른다.$$N(\\mu, \\frac{\\sigma^2}{n})$$표본의 수가 적을수록
24.[통계] 다중 검정

여러 개의 가설검정을 동시에 시행하는 것.이는 문제가 있다.예를 들어, 20개의 예측변수와 1개의 결과변수가 모두 임의로 생성되었다고 하자. 그리고 이걸 가지고 유의수준 5%에서 20번 다중검정을 시행한다고 하자.그러면 20번 수행에서 적어도 한 번은 '통계적으로 유의
25.[통계] 자유도

표본 데이터에서 계산된 통계량에 적용되며, 변화가 가능한 값의 개수이다.이전에 간단히 포스팅한 적이 있슴.\[통계] 표본평균과 모평균 (+표준오차, 자유도 )사실 데이터 과학자가 다루는 데이터의 경우 n이 굉장히 크기 때문에, n이나 n-1이나 별 차이 없다고 한다.다
26.[통계] 분산분석
도대체 누가 이걸 ANOVA로 줄일 생각을 했을까?A/B 두 그룹 이상의 그룹에 대한 차이를 검정할 때 사용하는 기법다중 검정의 경우 알파 인플레이션이 발생할 수 있는데, 때문에 각각 1회씩 비교하지 않는다.대신 전체적인 부분을 다루는 총괄검정에 속한다.독립변수의 갯수
27.[통계] 카이제곱검정(chi-squared test)
χ 카이제곱분포 이전에 카이제곱분포를 다루면서 분포와 검정에 대해 정리한 글이 있다. [통계] 카이제곱분포 (Chi-Squared Distribution) 간략하게 말하면, 자유도만큼의 샘플을 무작위로 뽑아 모두 제곱해서 더한 통계량의 분포가 카이제곱분포이다. 이는
28.[통계] 멀티암드 밴딧 알고리즘 (Multi Armed Bandits, MAB)

N개의 슬롯머신이 있고, 각각의 슬롯머신은 수익률이 다르다고 하자.그렇다면 어느 머신에 돈을 걸고 암(슬롯머신의 손잡이)를 내려야 할까?슬롯머신을 밴딧(강도), 손잡이를 암이라고 하고, 성공하기 위해서는 어느 슬롯머신을 노려야 하는지 구하는 알고리즘이다.A, B, C
29.[통계] 검정력, 효과크기와 표본크기

🖤 검정력 > 검정력(檢定力, statistical power)는 대립가설이 사실일 때, 이를 사실로서 결정할 확률이다. -위키백과 2종 오류가 "대립가설이 사실일 때, 이를 기각할 확률"이므로 $1-2종오류\,확률$이 된다. 🚨 영향을 미치는 요인 유의수준 (
30.[통계] 선형회귀
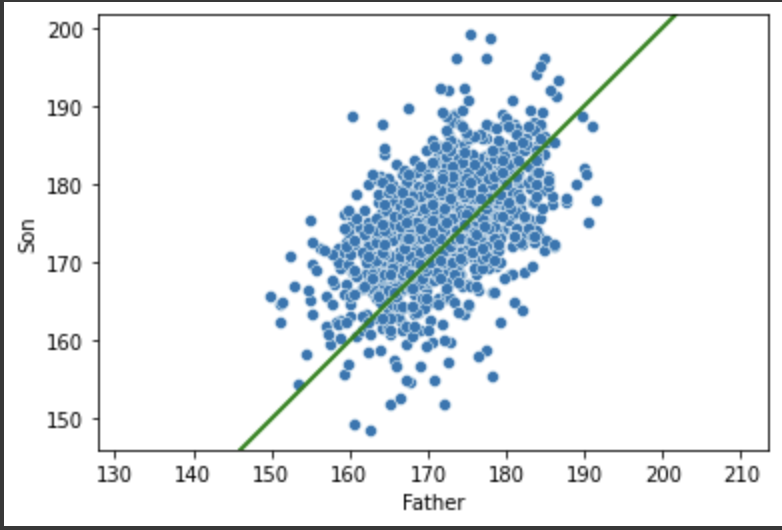
0. 선형회귀란? 변수 X와 Y의 관계를 정의하고, 그로부터 새로운 X에 대한 Y값을 예측하는 모델을 훈련하는 과정. 이는 문제-답이 주어져야 하는 지도 학습 (supervised learning)에 속한다. 또 데이터 과학과 통계학 사이의 중요 연결 고리는 이상 검출
31.[통계] 나이브 베이즈 알고리즘
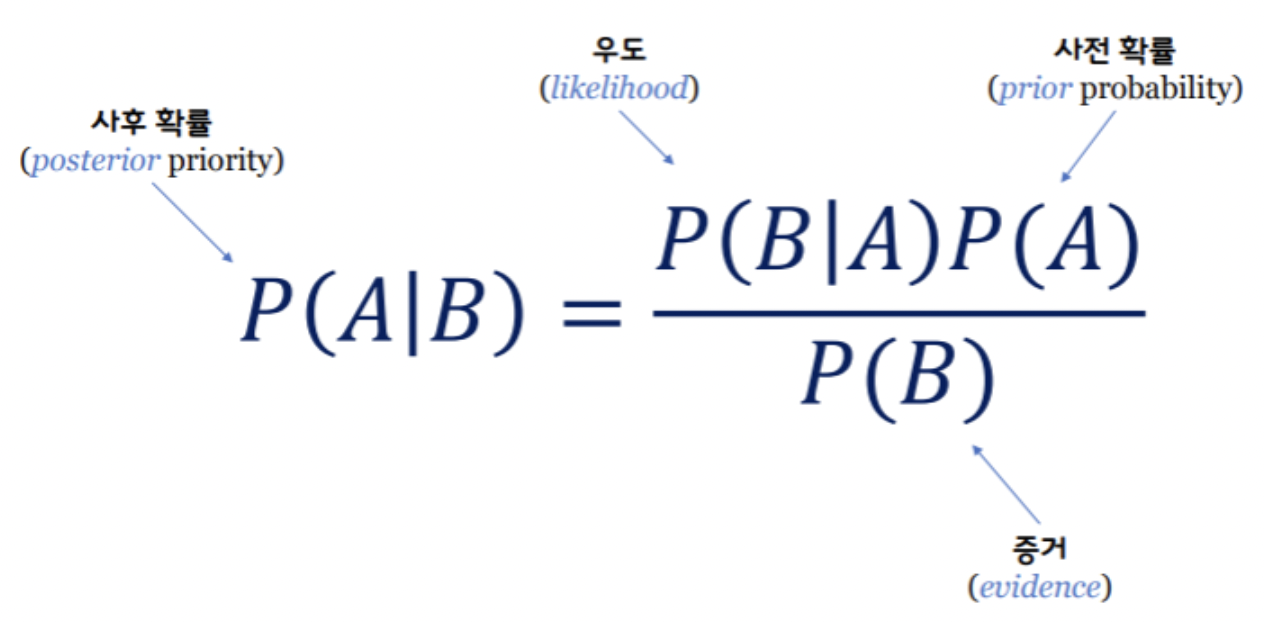
베이즈 정리. 이미지 출처 : 링크분류 알고리즘의 하나로, 주어진 결과에 대해 예측변숫값을 관찰할 확률로 예측변수 -> 결과를 예측하는 알고리즘이다.영단어 Naive의 뜻은 "순진한, 단순한, 천진난만한" 등의 뜻이 있다. 이는 원래 베이즈 분류가 빡빡하게 "모든 예측
32.[통계] 선형판별분석 (LDA)
트리, 로지스틱 회귀 등의 정교한 기법이 발명된 후로 많이 사용되지는 않지만, 주성분분석과 같은 분야에서 아직도 사용된다.데이터를 어느 한 축에 사영시켜 그룹이 더 잘 구분되는 직선을 찾는 것을 목표로 한다.아래 이미지에서는 LD2 축보다 LD1 축을 골라 분류하는 것
33.[통계] 로지스틱 회귀

다중선형회귀와 비슷하지만, 결과가 이진형 변수이다.로짓(logit) : $\\pm\\infin$ 범위에서 어떤 클래스에 속할지 확률을 정하는 함수오즈(odds) : 실패(0)에 대한 성공(1)비율로그 오즈 (log odds) : 변환 모델(선형)의 응답변수, 이 값으로
34.[통계] 분류 모델 평가
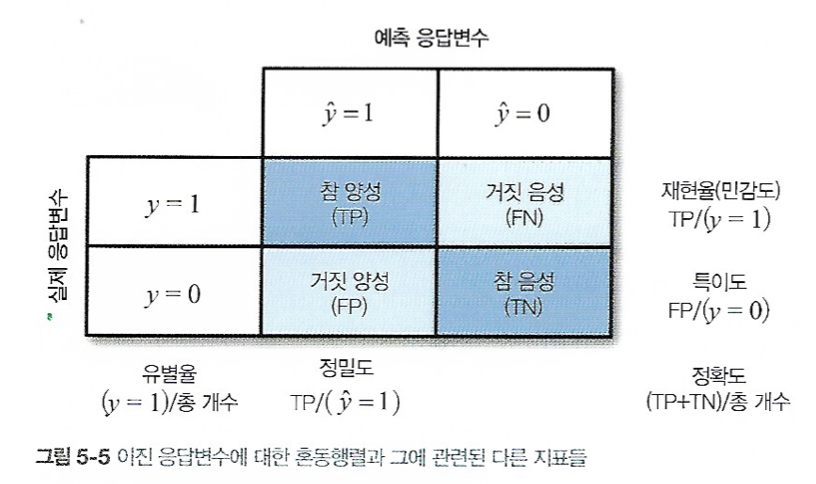
가장 간단한 분류 모델 평가는 정확도를 이용한 방법이다.$$정확도=\\frac{\\sum{참\\,양성+\\sum참\\,음성}}{표본크기}$$직관적으로 이해할 수 있다.분류 결과를 가장 잘 나타내는 행렬정밀도는 예측된 양성 결과의 정확도.$$정밀도=\\frac{\\sum
35.[통계] 불균형 데이터 다루기

데이터가 너무 적을 때, 예측 모델링 성능을 향상할 방법을 살펴보자.다수에 해당하는 데이터 클래스에서 과소표본추출을 통해 0과 1의 비율을 맞출 수 있다.이는 다수의 클래스는 중복된 데이터가 많을 것이다라는 개념인데, 생각해보면 당연하게 더 많은 쪽에 치우친 결과가 주
36.[통계] 비지도학습
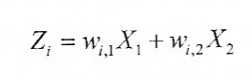
레이블링 과정 없이 데이터를 주고 모델을 훈련하는 과정데이터의 차원을 줄이는 데 사용두 변수 $X_1, X_2$에 대해 두 주성분 $Z_i$가 있다고 하자.이 때 $w$를 각각 성분의 부하라고 한다.(원래 변수를 주성분으로 변환할 때 사용한다)첫 주성분 $Z_1$은 전
37.[통계] k-평균 클러스터링
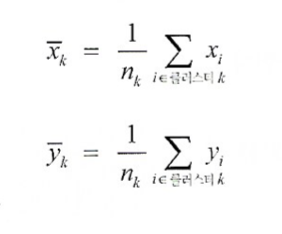
데이터를 $k$개의 군집으로 분류하는 방법클러스터의 중심 $\\bar{x_k}, \\bar{y_k}$는 다음처럼 결정된다.클러스터끼리는 최대한 멀어지도록 조정한다.이를 클러스터 내 제곱합 또는 SS라고 한다.SS가 최소가 되도록 군집을 분류하는 것이 k-평균 알고리즘이