📊 표본평균
표본평균이란, 모집단에서 표본추출법을 이용해 추출한 표본의 평균이다.
헷갈리면 안 되는 부분이, 모집단의 단일 표본 하나의 평균이다 !! 모든 표본의 평균값이 아님.
아래 사진은 표본평균과 표본분산, 표본표준편차에 대한 공식이다.
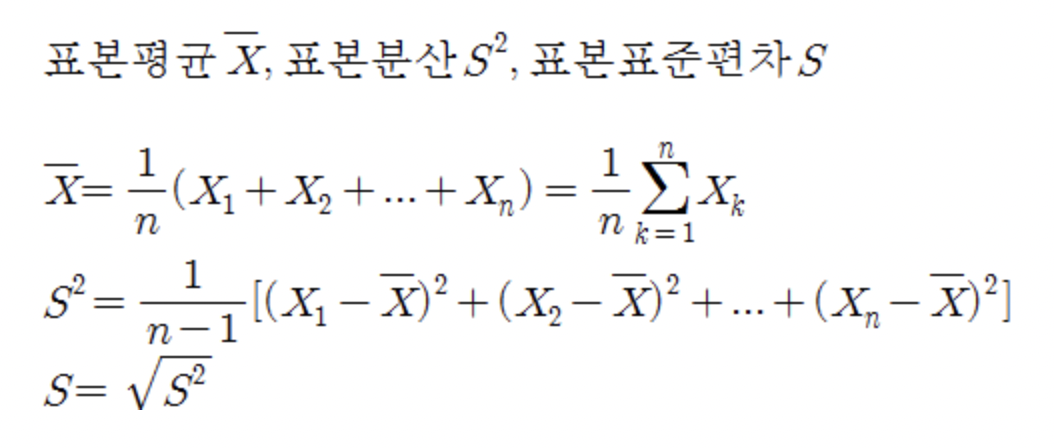
이 때 표본분산을 구할 때 으로 나누지 않고 로 나누게 되는데, 이는 모분산과의 차이를 줄이기 위함이라고 하며, 이 수를 자유도 (Degree of Freedom)라고 한다.
🚨표본평균을 구할 때는 그대로 으로 나눠야 한다 !!!🚨
사실 n이 크면 별 상관 없다고.
📊 자유도
통계적 추정을 할 때 표본자료 중 모집단에 대한 정보를 주는 독립적인 자료의 수를 말한다. - 위키피디아
포인트는 '독립적'. 모든 편차의 합은 0이 되어야 하는데, 이 경우 n번째 값은 편차의 합이 0이 되는 수로 독립적이 아니게 된다고 한다.
따라서 마지막 항은 독립적이지 않게 되고, 개의 항만이 자유도를 가지는 것.
이 클수록 과 유의미한 차이가 없다고 하고, 데이터 과학에서는 주로 큰 표본이나 모집단을 다루니 깊게 신경쓸 필요는 없다고 한다.
📊 모평균
모평균이란 모집단의 평균을 말한다.
다만 대부분의 모집단은 굉장히 크고 예측하기 어렵기 때문에, 주로 표본들의 값을 보고 추론한다.
여기서 표본평균들의 평균=모평균이라는 개념이 등장한다. 다만 이는 완전히 같을 수 없고, 모평균과의 차이를 표준오차라고 한다.
📚 표준오차
표준오차란 표본통계량의 표준편차이다.
표본편차 에 대해서, 표준오차의 식은 이 된다.
이 표준오차가 작을수록 표본의 대표성이 높아진다고 한다.
표준오차는 신뢰구간을 구할 때 혹은 가설검정에서 가설통계량을 계산할 때 사용된다.
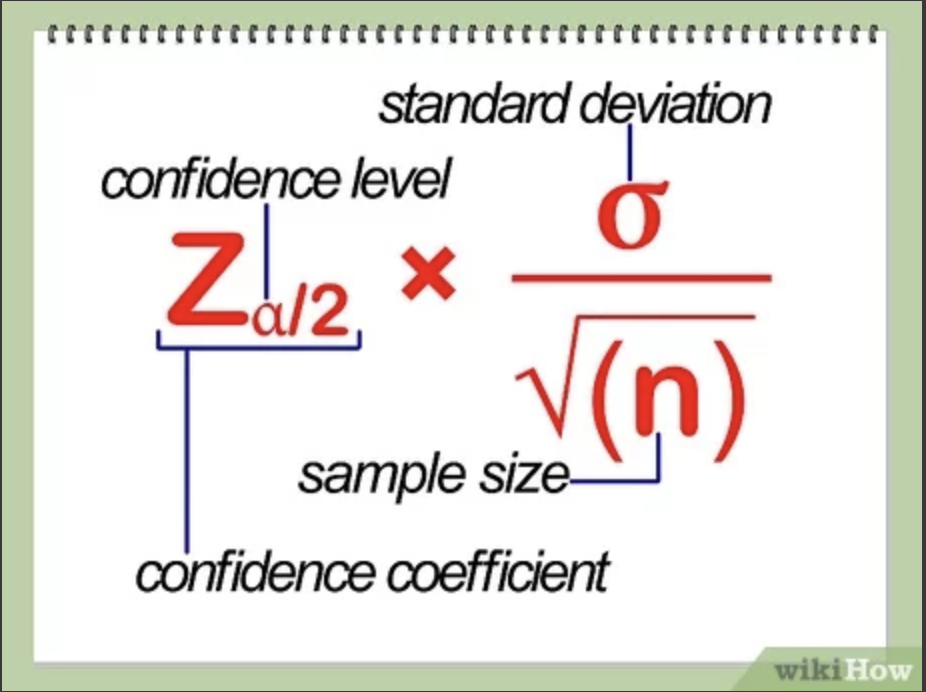
신뢰구간을 구하는 공식 출처 : wikiHow
🚨 증명 : 모분산을 라 하고, 표본분산을 라고 했을 때,
, 분산의 성질에 의해
따라서 표본평균의 표준편차는
