📚 Arrays
Set of homogenous data. 동일한 자료형으로 구성된 연결된 자료구조이다.
C에서도 C++에서도 자바에서도 변수에 어레이를 지정하면 해당 변수는 어레이의 첫 칸 주소 위치를 저장하게 된다.
int[] a = new int[4];이렇게 선언을 해주면
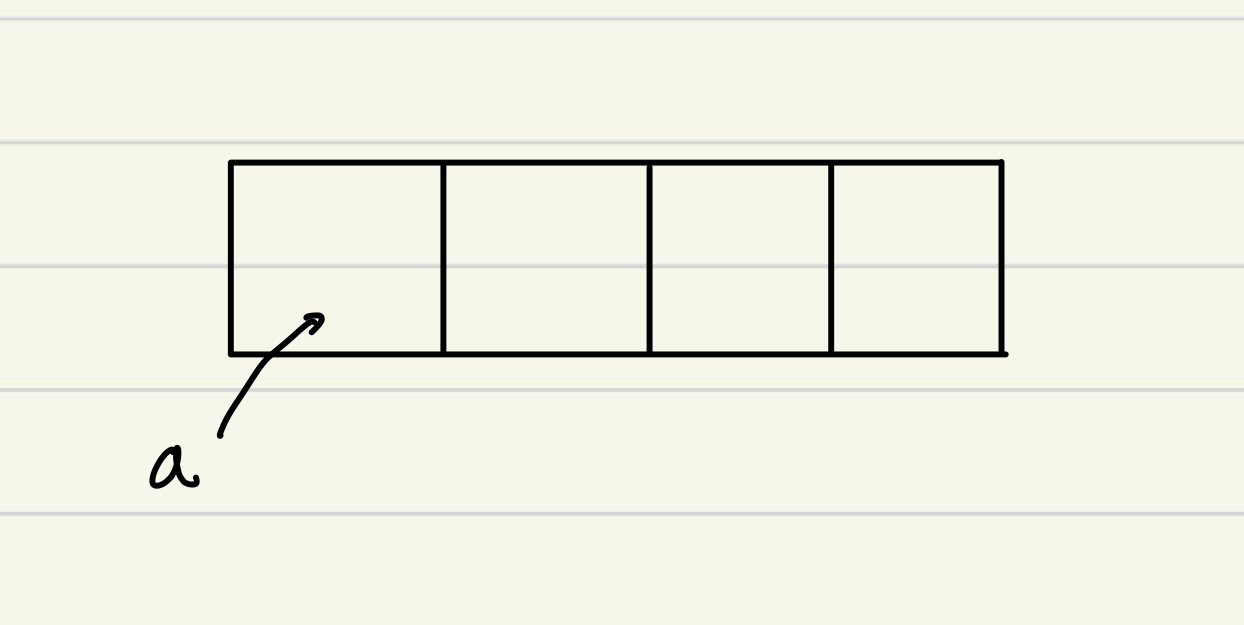
이렇게 메모리 공간에서 연속된 칸을 쓰게 된다.
📚 Indexing
Array 자료형의 가장 큰 특징이라면 정수를 통한 인덱싱이 가능하다는 것.
public class main {
public static void main(String[] args) {
int[] a = new int[4];
for (int i=0;i<4;i++)
a[i] = i+1;
}
}이렇게 되면 Array의 각 칸에 1~4가 들어가게 되는 것.
인덱스는 0부터 시작하는데, 그 이유는 위에서 말한 '주소' 의 개념에 있다.
메모리 공간을 곧바로 가리키고 있는 위치에서부터 데이터가 저장되기 때문.
C의 개념을 조금 빌리면, 포인터에 저장된 값의 접근은 아래와 비슷하게 처리된다.
a[i] = *(a+i)그러니까 저장 공간에 접근할 때 첫 번째 요소라고 1을 사용하지 않는 것.
포인터가 가리키는 곳에 첫 번째 값이 바로 저장되어 있기 때문이다.
📚 Time Complexity
배열의 값에 접근하는 것은 의 시간복잡도를 가진다. 그냥 주소+상수 연산이기 때문.
반면 Array의 삽입, 삭제의 시간 복잡도는 Unsorted인지 Sorted인지에 따라 다르다.
N은 배열의 요소라고 하자.
Unsorted
n개의 요소가 무질서로 배치되어 있다고 하자. 이 중 특정한 값을 찾으려면 배열을 전부 뒤지는 수밖에 없다. 그렇기에 탐색은 의 복잡도를 가진다.
삭제도 마찬가지다. 삭제하고 싶은 요소를 찾고, 해당 값을 지우고, 빈 칸을 채우기 위해 뒤에 있는 값들을 한 칸씩 앞으로 당겨야 한다.
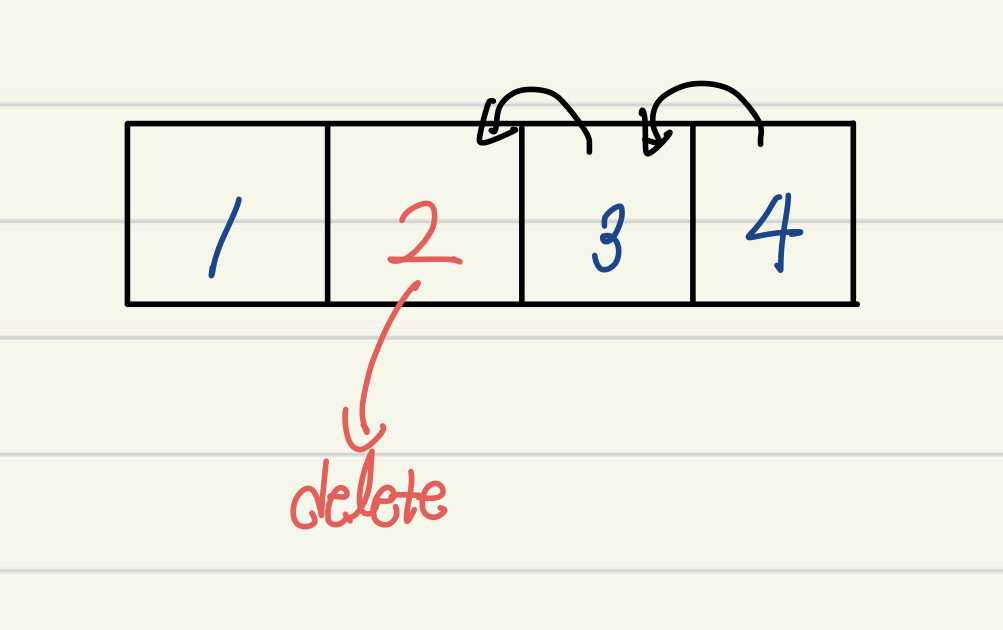
맨 앞에 있는 요소를 지우는 경우, 최대 N-1번의 교체 연산이 일어난다.
그렇기에 시간복잡도는 이 된다.
반면 삽입은 간단하다. 무질서한 상태이므로 걍 넣으면 된다. 배열에 접근하는 것은 의 시간복잡도이므로 마지막 인덱스에 접근 후 삽입하면 된다.
따라서 다음과 같이 정리가 가능하다.
Sorted
이 경우 탐색에는 O(logN), 삽입과 삭제에 O(n)의 시간이 걸리게 된다.
정렬된 요소 중 올바른 위치를 찾기 위해 최대 logN번 배열을 순회해야 하고,
알맞은 위치를 찾아 요소를 넣기 위해서 최대 n번 요소를 한 칸씩 뒤로 미뤄야 하기 때문이다.
탐색에 이 걸리는 이유는 Binary Search라는 알고리즘 덕분이다.
정렬 리스트의 경우, 찾는 값이 대충 어디에 있는지 알 수 있다.
간단하게 말하면 에서 식을 k에 대해 정리하면 logN이 나온다.
이 때 k는 비교연산 횟수인데, 한 번 비교할때마다 비교할 값이 반으로 줄어서 1/2를 k번 곱하면 마지막 하나가 나오는 것.
삭제 또한 Unsorted의 경우와 마찬가지로 삭제 후 뒤의 요소들을 땡겨오는 데 최대 n번의 순회가 발생한다.
logN보다 N이 복잡도가 높으므로 최종 복잡도는 O(N)이다.
그렇기 때문에 다음처럼 정리할 수 있다.
💻 구현
Unsorted Array
class UnsortedArray {
private int[] arr;
private int len;
private int n;
public UnsortedArray(int n) {
arr = new int[n];
this.n = n;
len = 0;
}
public int getValue(int index) {
if (index >= len || index < 0)
return -1;
return (arr[index]);
}
public boolean insert(int n) {
if (isFull())
return false;
arr[len++] = n;
return true;
}
public boolean delete(int n) {
int i;
if (isEmpty())
return false;
for (i=0;i<len;i++)
if (arr[i] == n)
break;
if (i == len) return false;
for (;i<len-1;i++)
arr[i] = arr[i+1];
len--;
return true;
}
public boolean isFull() {
return (n == len);
}
public boolean isEmpty() {
return (len == 0);
}
public void printAll() {
for (int i=0;i<len;i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
Unosorted의 경우 구현이 쉽다. insertion에서 그냥 마지막 위치에 넣어주면 되고, Deletion에서 한 칸씩 당겨주는 것만 주의하면 되기 때문.
Sorted Array
class SortedArray {
private int[] arr;
private int len;
private int n;
public SortedArray(int n) {
arr = new int[n];
this.n = n;
len = 0;
}
public int getValue(int index) {
if (index >= len || index < 0)
return -1;
return (arr[index]);
}
public boolean insert(int n) {
if (isFull())
return false;
int idx, tmp;
idx = binarySearch(n);
System.out.println("idx : " + idx);
for (int i=len;i>idx;i--) {
arr[i] = arr[i-1];
}
arr[idx] = n;
len++;
printAll();
return true;
}
public boolean delete(int n) {
if (isEmpty())
return false;
int idx, tmp;
idx = binarySearch(n);
if (arr[idx] != n)
return false;
for (int i=idx;i<len-1;i++)
arr[i] = arr[i+1];
len--;
return true;
}
public boolean isFull() {
return (n == len);
}
public boolean isEmpty() {
return (len == 0);
}
public int binarySearch(int v) {
int left, right, mid;
if (isEmpty())
return 0;
left = 0;
right = len-1;
mid = (left + right)/2;
while (left < right) {
if (arr[mid] == v)
return mid;
else if (arr[mid] > v)
right = mid-1;
else if (arr[mid] < v)
left = mid+1;
mid = (left + right)/2;
}
if (arr[mid] < v)
return mid+1;
return mid;
}
public void printAll() {
for (int i=0;i<len;i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
하지만 Sorted의 경우는 binary Search를 구현하고, 그를 통해서 insert나 delete할 때 적절한 인덱스를 잘 구해야 하기 때문에 번거로워진다.
binarySearch 함수에 arr[mid] < v인 경우만 mid+1을 하는 이유는 arr[mid]의 값이 v보다 작을지 클지 알 수 없기 때문인데, 작은 경우에는 그냥 해당 인덱스에 값을 넣고 오른쪽으로 당겨야 하고, 큰 경우에는 해당 인덱스의 오른쪽부터 당겨야 하기 때문.
⌛️ Time Complexity Check
public class main{
public static void main(String[] args) {
int max = 10000;
UnsortedArray s = new UnsortedArray(max);
long start = System.nanoTime();
for (int i=0; i<max; i++)
s.insert(i);
long end = System.nanoTime();
System.out.println("Unsorted insertion 수행시간: " + (end - start) + " ns");
start = System.nanoTime();
for (int i=max-1; i>=0; i--)
s.delete(i);
end = System.nanoTime();
System.out.println("Unsorted deletion 수행시간: " + (end - start) + " ns");
SortedArray a = new SortedArray(max);
start = System.nanoTime();
for (int i=max-1; i>=0; i--)
a.insert(i);
end = System.nanoTime();
System.out.println("Sorted insertion 수행시간: " + (end - start) + " ns");
start = System.nanoTime();
for (int i=0; i<max; i++)
a.delete(i);
end = System.nanoTime();
System.out.println("Sorted deletion 수행시간: " + (end - start) + " ns");
}
}
해당 테스트 코드를 통해 실제로 수행시간이 얼마나 차이나나 비교하자.
(Java의 nanoTime() 메서드는 JVM마다 측정 시간이 다를 수 있으므로, 본인과 시간이 다르게 출력될 수 있다.)
배열의 크기는 10000개로 설정하고 진행했다.

결과를 보니, 확실히 복잡도가 O(1)인 Unsorted insertion이 가장 짧은 시간을 보였다.
그리고 O(n)의 복잡도를 가지는 Unsorted deletion, sorted insertion, sorted deletion은 비슷한 시간을 소요했는데, 대략적으로 10000배의 시간이 걸린 걸 보면 N의 상수배에 가깝다.
또한 max 변수의 크기를 늘려보면 늘릴수록 O(1) 코드와 O(n) 코드의 실행 시간이 압도적으로 차이가 날 것이다. 본인 기준 0을 두 개만 더 붙여도 Unsorted deletion까지 한참 걸린다.
