📚 Binary Search Tree

Binary Search Tree(이진탐색트리) 란 다음과 같이 정의된다.

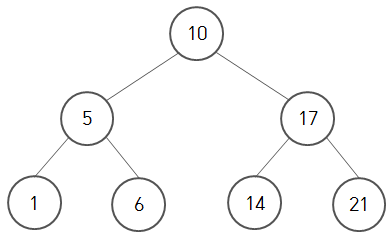
• 빈 트리 혹은 아래 사항을 만족하는 Binary Tree
• root가 키값을 가지고 있다고 하면 왼쪽 subtree의 값은 모두 key보다 작고, 오른쪽은 큰 Binary Tree
• 양쪽 Subtree 모두 binary search tree여야 함

이 때 노드의 각 값은 distinct하다.

⚙️ Functions

• insert : BST에 요소를 삽입하는 것.
• delete : 특정 요소의 삭제

기능은 아직까지는 이정도로 끝.

주의해야 할 점으로는 delete가 있다. Insert는 직관적으로 이해가 쉽다. 그냥 내려가면서 알맞은 자리에 넣어주면 된다.

하지만 delete의 경우는 세 가지 경우를 고려해야 한다. child가 없을 때, child가 하나일 때, child가 둘일 때.

child가 없을 때는 그냥 이전 노드에서 해당 child를 null로 바꿔주면 된다.

child가 하나인 노드를 삭제할 때는 노드의 child를 parent에 이어줘야 한다. 이 때, 방향은 그대로 유지되어야 BST의 성질도 유지되고 붕괴되지 않는다.

child가 둘인 노드를 삭제할 때가 가장 복잡하다. 한 방법은 노드의 왼쪽 subtree에서 가장 큰 값을 찾아 해당 값을 현재 노드의 값으로 복사하고, 복사해온 원본 노드를 삭제하는 것. 이게 가능한 이유는 왼쪽 subtree에서 가장 큰 값 기준으로 왼쪽 subtree의 모든 값이 작을 것이므로 BST 성질이 위반되지 않는다.
물론 반대로 오른쪽에서 가장 작은 값을 복사해오는 것도 가능하다.

두 기능 모두 재귀를 통해 구현해보자.

💻 Implementation

class BST {
	private BTNode root;

	public BST() {
		root = null;
	}

	public void insert(int x) {
		root = doInsert(root, x);
	}

	public BTNode doInsert(BTNode cur, int x) {
		if (cur == null) {
			BTNode newNode = new BTNode();
			newNode.data = x;
			return (newNode);
		}
		if (cur.data > x)
			cur.left = doInsert(cur.left, x);
		else
			cur.right = doInsert(cur.right, x);
		return (cur);
	}


	public void delete(int x) {
		if (isEmpty()) return;
		root = doDelete(root, x);
	}

	public BTNode doDelete(BTNode cur, int x) {
		if (cur == null) return null;
		if (x < cur.data)
			cur.left = doDelete(cur.left, x);
		else if (x > cur.data)
			cur.right = doDelete(cur.right, x);
		else {
			if (cur.left != null && cur.right != null) {
				int tmp;

				tmp = getMax(cur.left).data;
				cur.data = tmp;
				cur.left = doDelete(cur.left, tmp);
				return cur;
			}
			else if (cur.left != null)
				return cur.left;
			else if (cur.right != null)
				return cur.right;
			else
				return null;
		}
		return cur;
	}
	public BTNode getMax(BTNode cur) {
		while (cur.right != null)
			cur = cur.right;
		return cur;
	}

	public void inOrder() {
		doInOrder(root);
		System.out.println();
	}

	public void doInOrder(BTNode cur) {
		if (cur == null) return;
		doInOrder(cur.left);
		System.out.print(cur.data + " ");
		doInOrder(cur.right);
	}


	public boolean isEmpty() {
		return (root == null);
	}
}

사실 처음에는 반복문을 통해 구현하려 했는데, 너무 번거로워 재귀를 통해서 구현했다.

⌛️ Time Complexity

• search : O(h)
  : 이진탐색트리에서의 검색은 최대 h개의 노드를 검사하기 때문에 O(h)이다. 이 때 h는 이진탐색트리의 높이이다.
• insertion : O(h)
  : 검색에 O(h), 삽입에 O(1)이므로 O(h)가 된다.
• deletion : O(h)
  : 역시 최악의 경우 검색에 O(h), 삭제에 O(1) 또는 중간 노드일 때 O(a+b=h) 꼴이 된다.

하지만 h는 트리가 지나치게 치우치지 않는다면 평균적으로 logn의 높이를 가지게 된다.

따라서 평균적으로는 셋 모두 logN의 시간복잡도를 가진다.
최악의 경우에는 일렬인 이진탐색트리이므로 O(n)이 된다.

Iterator 구현

재귀보다는 스택을 이용해서 구현해보겠다.

InOrder

InOrder의 경우, left-root-right 순서이기 때문에 왼쪽 라인을 전부 push해주고 시작한다.
그리고 next로 넘어가기 위해 pop할 때마다 해당 노드가 오른쪽 자식을 가지고 있는지 검사해주면 된다.

class InIter {
	private BST bt;
	private	LLStack<BTNode> s;

	public InIter(BST b, BTNode root) {
		bt = b;
		s = new LLStack<BTNode>();
		pushAllLeft(root);
	}

	public boolean atEnd() {
		return (s.isEmpty());
	}

	public void pushAllLeft(BTNode cur) {
		while (cur != null) {
			s.push(cur);
			cur = cur.left;
		}
	}

	public void next() {
		if (atEnd()) return ;
		BTNode prev = s.pop();
		if (prev.right != null)
			pushAllLeft(prev.right);
	}

	public int getValue() {
		if (atEnd()) return -1;
		return (s.peek().data);
	}
}

PreOrder

PreOrder가 가장 쉽다. root-left-right 순서이므로, 처음에는 root을 스택에 넣어주고, next할 때마다 오른쪽 왼쪽 자식노드가 존재하는지 확인 후 넣어주면 된다.

class PreIter {
	private BST bt;
	private LLStack<BTNode> s;

	public PreIter(BST b, BTNode root) {
		s = new LLStack<BTNode>();
		bt = b;
		s.push(root);
	}

	public boolean atEnd() {
		return (s.isEmpty());
	}

	public int getValue() {
		if (atEnd()) return -1;
		return (s.peek().data);
	}

	public void next() {
		if (atEnd()) return ;
		BTNode prev = s.pop();
		if (prev.right != null) s.push(prev.right);
		if (prev.left != null) s.push(prev.left);
	}
}

PostOrder

약간 어려운데, left-right-root 순서이기 때문에 가장 왼쪽 '줄' 이 되는 subtree를 전부 넣어준다고 생각한다.
그리고 pop을 할 때 해당 노드가 왼쪽 자식이었다면 오른쪽 노드 기준 다시 가장 왼쪽 '줄' 을 넣어주면 된다.
(헷갈린다 ㅋㅋ)

class PostIter {
	private LLStack<BTNode> s;
	private BST bt;

	public PostIter(BST b, BTNode root)  {
		bt = b;
		s = new LLStack<BTNode>();
		pushMostLeft(root);
	}

	public void pushMostLeft(BTNode cur) {
		while (cur != null) {
			s.push(cur);
			if (cur.left == null) cur = cur.right;
			else cur = cur.left;
		}
	}

	public int getValue() {
		if (atEnd()) return -1;
		return (s.peek().data);
	}

	public void next() {
		if (atEnd()) return;
		BTNode prev = s.pop();
		if (s.isEmpty() == false && s.peek().left == prev)
			pushMostLeft(s.peek().right);
	}

	public boolean atEnd() {
		return (s.isEmpty());
	}

}