📚 Tree

트리는 자료구조의 일종으로, root에서부터 자식들이 뻗어나가는 모습이 나무와 닮아 붙은 이름이다. 대표적으로 이진 트리 (자식이 2개인 트리) 가 유명하다.

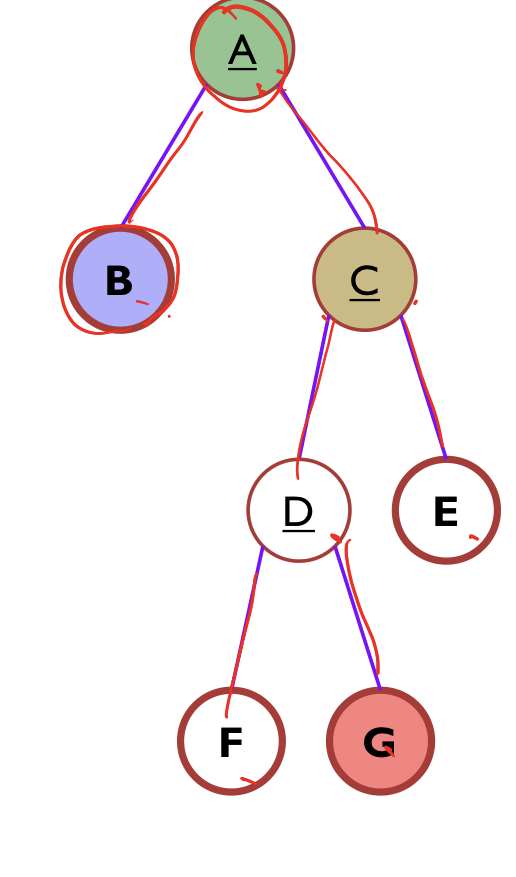
정의

• 하나 이상의 유한한 노드의 집합
• root 노드라는 식별 가능한 노드가 있다 (최상위 노드)
• 나머지 노드도 ${T}_1, T_2...$로 분할될 수 있는데, 각자의 분할된 집합도 Tree이다. 이를 root의 Subtree라고 한다.

용어

• Root : 트리의 가장 위에 있는, 다른 노드와 구별되는 노드

• Edge : 두 노드를 잇는 간선

• child : 노드 바로 아래에 존재하는 노드

• Parent : 노드 바로 위에 존재하는 노드

• Descendant : 노드의 subtree에 존재하는 노드 (child는 아님)

• Ancestor : 노드 위에 존재하는 노드

• Leaf Node : 자식이 없는 말단 노드

• Degree : 노드가 가지는 child 노드의 개수

• path : 두 노드를 연결하는 길

• Level : root로부터 해당 노드까지 path의 길이

• Height : 최대 Level의 크기

💻 Internal Implementation

트리의 최대 degree를 알고 있다면 Node에 그만큼의 포인터를 넣어주면서 내부적으로 구현하기 쉽다.

만약 이진 트리라면

class BTNode {
	public int data;
	public BTNode left;
	public BTNode right;
}

이렇게 구현할 수 있다.

만약에 parent도 필요한 트리라면

class BTNode {
	public int data;
	public BTNode left;
	public BTNode right;
	public BTNode parent;
}

이렇게 간단하게 구현할 수 있고!

트리의 형식이 정형화되어 있는 건 아니므로 다양한 내부 구현 방법이 있다.

📚 Binary Tree

Binary Tree(이진 트리) 는 자식이 딱 두 개인 트리이다.

성질

• 레벨 i 한정 최대 ${2^i}$ 개의 노드를 가진다.

• 높이 k의 이진 트리는 ${2^{k+1}-1}$개의 노드를 가질 수 있다.

• Full Binary Tree는 ${2^{k+1}-1}$개의 노드를 가지는 높이 k의 이진 트리이다. (걍 꽉 차면 그게 Full이다)

• 이진 트리에서는 아래와 같이 왼쪽부터 노드에 Numbering을 할 수 있다.
  

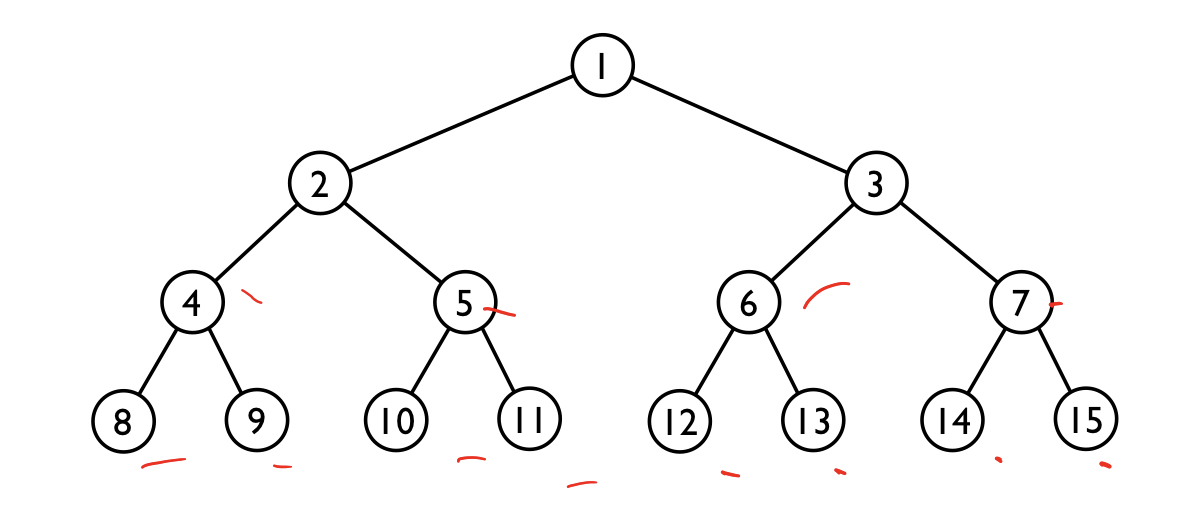
이렇게 했을 때, n개의 노드에 대해 1~n까지의 넘버링이 가능하면 그것을 Complete Binary Tree라고 한다.
쉽게 말하면 왼쪽부터 세므로 오른쪽 아래만 비어있을 수 있는 것.

💻 Implementation

Linked List 의 경우는 아까 봤고, 이진 트리는 Array로도 구현할 수 있다.

Array Implementation

Node numbering scheme의 번호를 인덱스라 생각하자.

• 이 경우 root는 arr[1] 에 위치한다 (0은 계산하기 번거로워 쓰지 않는다)
• i번째 노드의 left child는 [2i] 번째 인덱스에, right child는 [2i+1]번째 인덱스에 있다.
• 반대로 parent는 무관하게 [i/2]번째 노드에 있다.

Traversal

Traversal은 트리를 순회하는 방법이다. 세 가지 방법이 있다.

• InOrder : left-root-right 순서로 방문한다.
• PreOrder : root-left-right 순서로 방문한다.
• PostOrder : left-right-root 순서로 방문한다.

구현

아래와 같은 트리가 있다고 해보자.

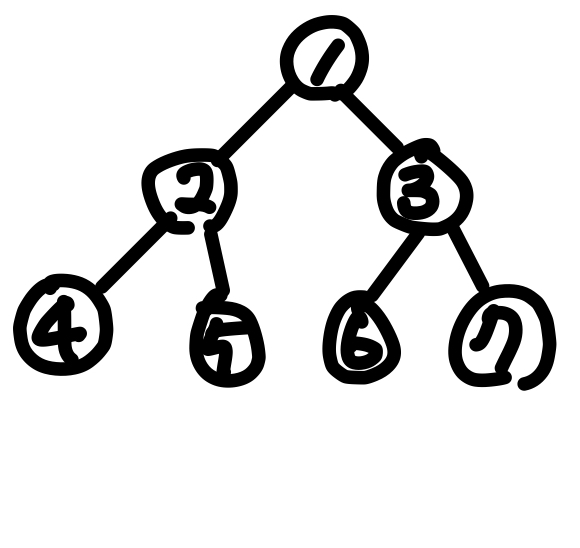
얘를 방문한다.

InOrder의 재귀 구현

	public void inOrder() {
		doInOrder(root);
		System.out.println();
	}

	public void doInOrder(BTNode cur) {
		if (cur == null) return ;
		doInOrder(cur.left);
		System.out.print(cur.data + " ");
		doInOrder(cur.right);
	}

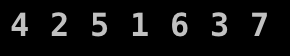
왼쪽 Subtree-현재 노드 - 오른쪽 Subtree 순서이므로 맞다.

PreOrder의 재귀 구현

	public void preOrder() {
		doPreOrder(root);
		System.out.println();
	}

	public void doPreOrder(BTNode cur) {
		if (cur == null) return ;
		System.out.print(cur.data + " ");
		doPreOrder(cur.left);
		doPreOrder(cur.right);
	}

현재 노드 - 왼쪽 SubTree - 오른쪽 SubTree.

PostOrder의 재귀 구현

	public void postOrder() {
		doPostOrder(root);
		System.out.println();
	}

	public void doPostOrder(BTNode cur) {
		if (cur == null) return ;
		doPostOrder(cur.left);
		doPostOrder(cur.right);
		System.out.print(cur.data + " ");
	}

역시 왼쪽-오른쪽-현재 순서이므로 맞다.

InOrder의 스택 구현

사실 스택 구현이 재귀보다 훨씬 복잡하다. 학교 강의에서는 재귀를 아예 다루지 않았는데, 너무 쉬워서인 것 같기도 ...

일단 BTree 클래스에 스택 변수 s를 추가해주고 시작하자.
그리고 아래처럼 구현하면 된다.

	public void pushAllLeft(BTNode cur) {
		while (cur != null) {	
			s.push(cur);
			cur = cur.left;
		}
	}
	public void inOrder() {
		BTNode cur = root;

		pushAllLeft(cur);
		while (!s.isEmpty()) {
			cur = s.pop();
			System.out.print(cur.data + " ");
			if (cur.right != null) pushAllLeft(cur.right);
		}
		System.out.println();
	}

pushAllLeft 함수는 해당 노드 기준 왼쪽 child가 null이 될 때까지 왼쪽만 모두 넣는다. 그러면 시작할 때부터 가장 왼쪽 leaf node부터 시작될테고, 만약 오른쪽 자식이 존재한다면 그 오른쪽 노드로 넘어가주면 된다. 재귀랑 비슷한 개념이지만 왼쪽을 모두 넣어서 헷갈리긴 한다.
오른쪽 노드로 가서도 왼쪽 subtree부터 방문해야 하므로 pushAllLeft를 호출해준다.
divide and conquer를 생각하면 될 듯.

잘 나오는 걸 알 수 있다.

PreOrder의 스택 구현

	public void preOrder() {
		BTNode cur = root;
		s.push(cur);
		while (!s.isEmpty()) {
			cur = s.pop();
			System.out.print(cur.data + " ");
			if (cur.right != null) s.push(cur.right);
			if (cur.left != null) s.push(cur.left);
		}
		System.out.println();
	}

얘는 보조 함수가 필요 없다. 간단!