📚 Queue

FIFO(First In First Out)이라는 특징을 가지고 있다.
Array Representation과 Linked List Representation이 둘 다 가능하다.

🎲 Functions

기능이 비교적 간단한 편.

• enqueue : 큐에 요소를 삽입한다.
• dequeue : 큐의 제일 앞의 요소를 제거하고 해당 값을 반환한다.
• isFull : 큐가 가득 찼는지 확인한다.
• isEmpty : 큐가 비었는지 확인한다.

💻 Implementation

Array Implementation

구현 전에, 주의해야 할 점이 있다.
첫째, 인덱싱을 하게 된다면 리스트의 앞에서부터 요소를 넣고 삭제하게 될텐데, 그런 경우 배열의 전체 크기를 사용하기 어렵다.

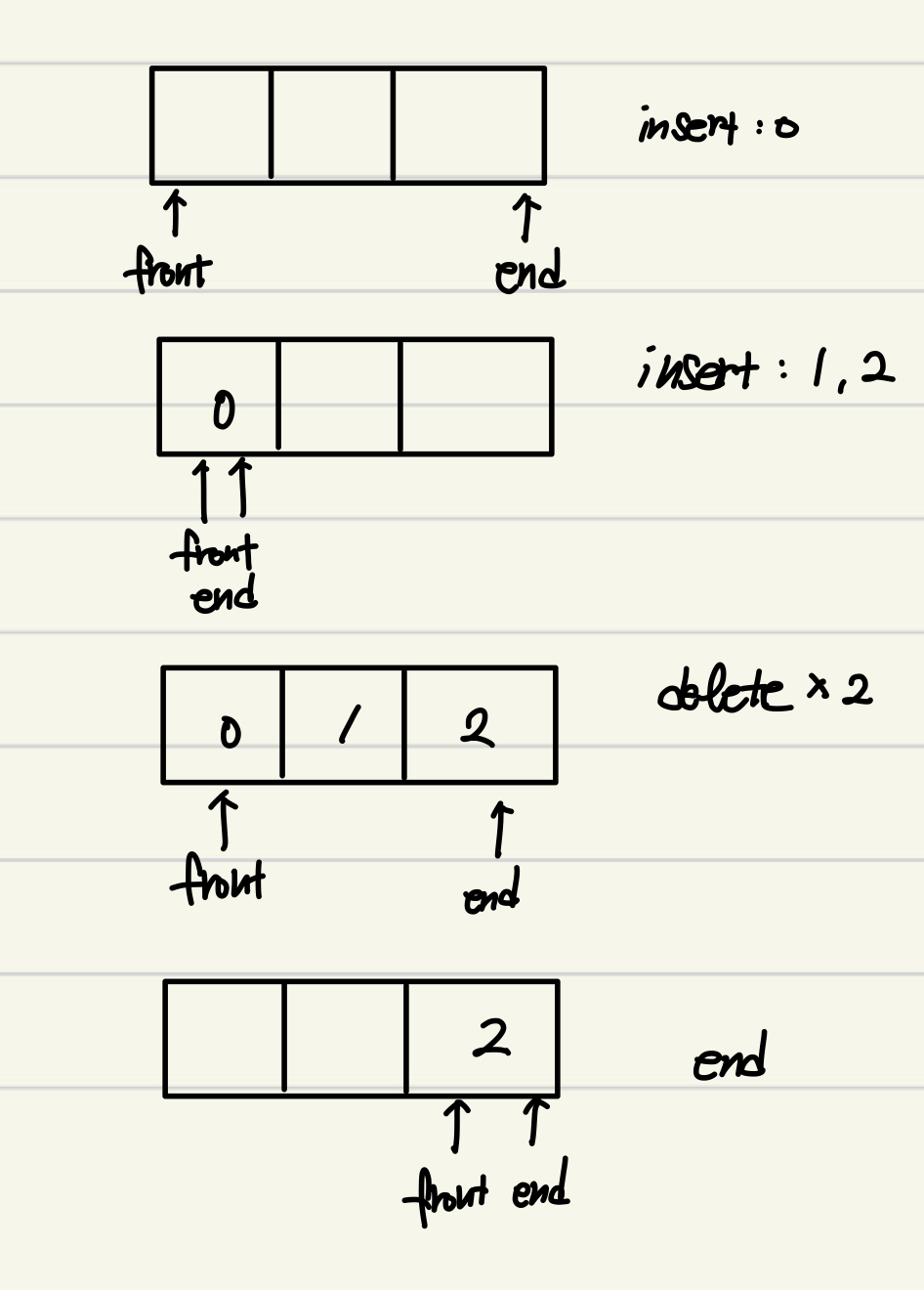
위 그림은 0,1,2를 enqueue하고 dequeue를 2번 진행한 결과이다.
첫째, 두번 삭제 후 front와 end가 이미 배열의 끝으로 와버려서 큐를 이용할 수 없다.
그렇기 때문에 큐를 일종의 Circular한 구조체로 구현해야 한다.
front 대신 (front % size) 를 쓰는 식이다. 그럼 첫 번째 문제 해결이다.

하지만 다른 문제가 생긴다. 그림 1에서 보면 큐가 비어있는 조건은 (end+1)%size == front이다.
큐가 꽉 차 있는 조건은 그림 3에서 (end+1)%size == front이다. 두 조건이 중복되기에, 실제로 해당 값일때 우리는 큐가 비어있는지 꽉 차있는지 구별할 수가 없다.

이에 대한 해결책은 큐의 마지막 한 칸을 쓰지 않는 것이다. (end+2)%size == front일 때 큐가 꽉 찼다고 판단해버리는 것이다.

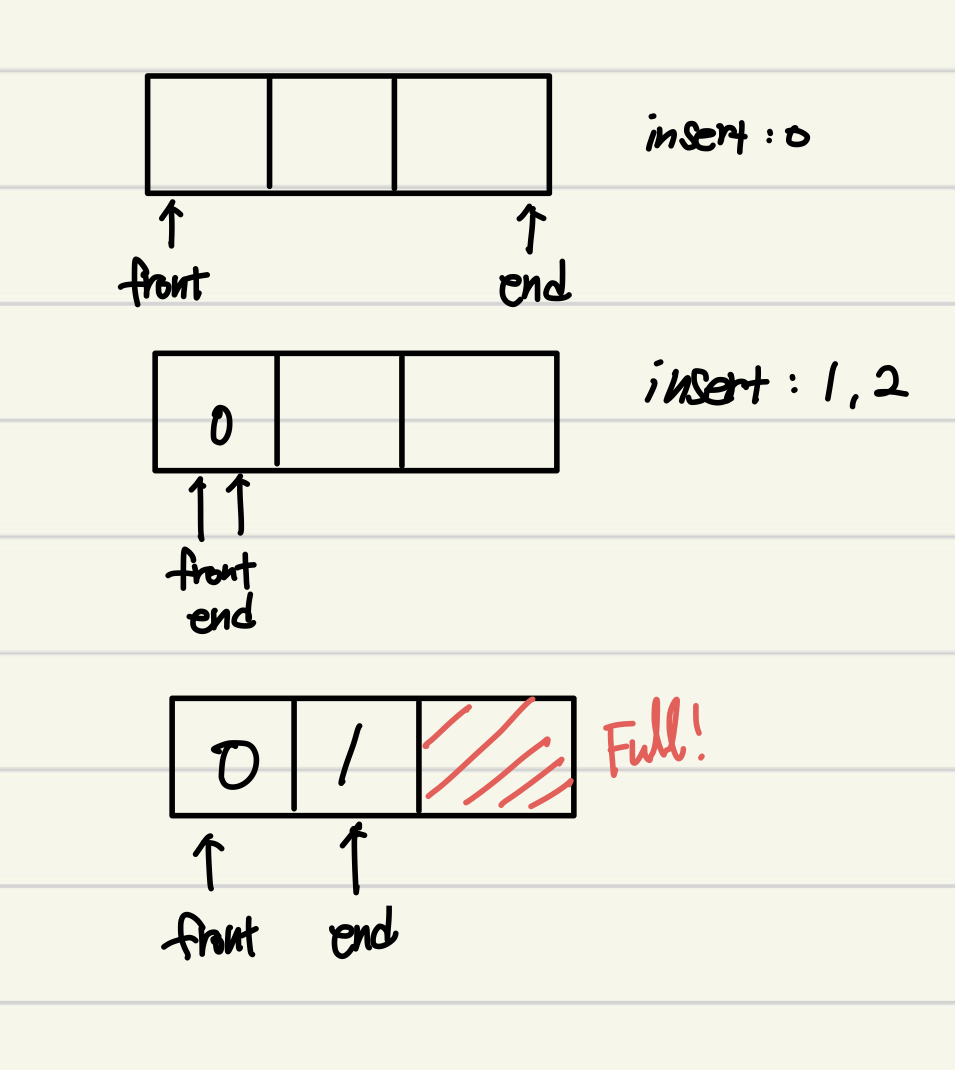
이러면 크기 3인 큐에서 2칸밖에 사용할 수 없지만, 중복 조건 문제를 해결할 수 있다.

물론 이건 원시적인 형태의 큐이고, 해결하려면 얼마든지 다른 변수를 추가해서 해결할 수 있다. 총 삽입된 요소의 수를 세는 변수를 넣는다던지 해서.

해당 고려사항을 모두 고려해서 코드로 구현하면 다음과 같다.

class ArrayQueue {
	private int front;
	private int end;
	private int size;
	private int[] arr;

	public ArrayQueue(int n) {
		front = end;
		end = n-1;
		size = n;
		arr = new int[n];
	}

	public void enqueue(int x) {
		if (isFull()) return ;
		arr[(++end%size)] = x;
	}

	public int dequeue() {
		if (isEmpty()) return -1;
		return (arr[(front++ % size)]);
	}

	public boolean isEmpty() {
		return ((end+1)%size == (front%size));
	}

	public boolean isFull() {
		return ((end+2)%size == (front%size));
	}
}

이러면 원형 큐가 잘 동작할 수 있다.

Linked List Implementation

연결 리스트로 구현하는 경우는 훨씬 난이도가 쉽다.
원형을 고려할 필요도 없고, 연결 리스트의 기존 기능을 활용해서 코딩하면 된다.

class LLQueue<T> {
	private LinkedList<T> l;

	public LLQueue() {
		l = new LinkedList<T>();
	}

	public void enqueue(T x) {
		l.insertAtEnd(x);
	}

	public T dequeue() {
		if (isEmpty()) return null;
		return (l.deleteAtFront());
	}

	public boolean isEmpty() {
		return (l.isEmpty());
	}
}

연결 리스트이므로 isFull() 을 따로 구현할 필요도 없음 !
(물론 동적 할당이 터질 수 있는 실제 환경에서는 null가드를 해줘야 하긴 할거다)

⌛️ Time Complexity

• enqueue : O(1)
  Array 구현에서는 단순히 인덱싱을 통해 실행할 수 있고, Linked List에서도 InsertAtEnd() 함수를 통해서 구현할 수 있다. 두 경우 모두 O(1)의 시간복잡도를 가진다.

• dequeue : O(1)
  역시 Array이 경우 인덱싱, Linked List에서는 DeleteAtFront() 함수를 통해 실행된다. 두 경우 모두 O(1).

LinkedList 구현에서는 주로 리스트의 앞을 front, 뒤를 End로 써서 뒤로 들어와서 앞으로 나가는 형식으로 구현하는 게 흔한데, 이는 LinkedList 게시물에서도 언급했듯 DeleteAtEnd() 메서드의 구현이 번거롭기 때문

• isFull, isEmpty : O(1)
  단순히 비교문을 통해 반환하면 된다.