📚 k-평균 클러스터링

• 데이터를 $k$개의 군집으로 분류하는 방법

• 클러스터의 중심 $\bar{x_k}, \bar{y_k}$는 다음처럼 결정된다.
  

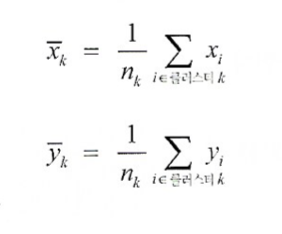
• 클러스터끼리는 최대한 멀어지도록 조정한다.

• 이를 클러스터 내 제곱합 또는 SS라고 한다.
  
  

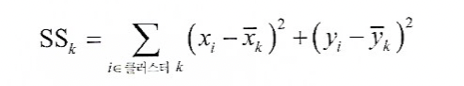
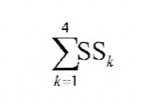
• SS가 최소가 되도록 군집을 분류하는 것이 k-평균 알고리즘이 된다.

k-평균 알고리즘

• 일반적으로 $k$평균 알고리즘은 $p$개의 변수 $X_1, ..., X_p$에 적용할 수 있다.
• 정확한 해를 계산하기는 어려우므로, 사용자가 미리 정해준 k 평균 초깃값과 클러스터의 개수 k를 가지고 아래 과정을 반복한다.
  • 각 레코드를 가장 가까운 클러스터에 할당한다.
  • 클러스터의 중심을 클러스터에 속한 레코드들의 중심으로 옮긴다.

반복이 더이상 일어나지 않으면 알고리즘이 수렴한 것이다.
이 과정은 항상 최적 답을 주지는 않으므로 초깃값을 수정하며 반복해야 한다.

클러스터 해석

• kmeans 에서 가장 중요한 출력은 클러스터의 크기와 평균이다.
• 클러스터의 크기가 유난히 이상한 클러스터가 존재한다면, 이는 특잇값이나 이상치가 있다는 뜻이다.

클러스터 개수 선정

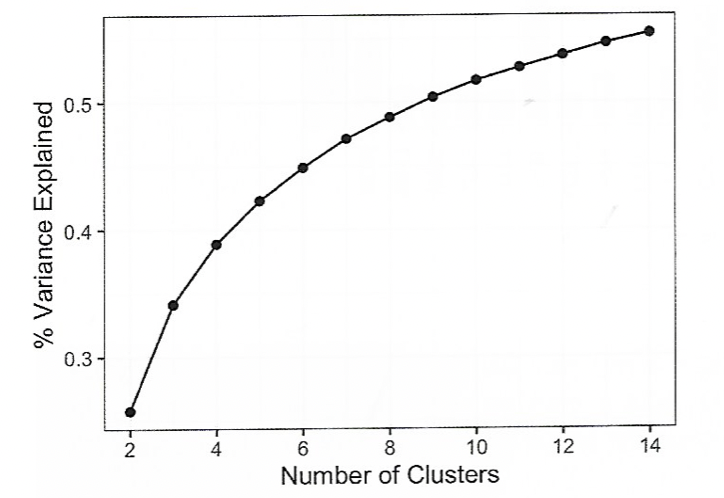
• 팔꿈치 방법은 언제 클러스터 세트가 데이터의 분산을 '대부분' 설명하는지 알 수 있는 방법이다.
• 클러스터를 추가할수록 각 클러스터의 분산의 기여도가 작아진다.
• 분산의 증가율이 급격한 부분이 적절한 클러스터의 개수가 된다.
  

📚 계층적 클러스터링

• $n$개의 레코드와 $p$개의 변수가 있는 데이터에 대헤 계층적 클러스터링을 적용할 수 있다.
• 다음 두 가지 요소를 기본으로 한다.
  
• 계층적 클러스터링은 각 레코드를 클러스터로 지정한 상태에서 시작하고 가까운 클러스터를 결합해나간다.

덴드로그램

• 계층적 클러스터링은 시각화가 가능하다.
  

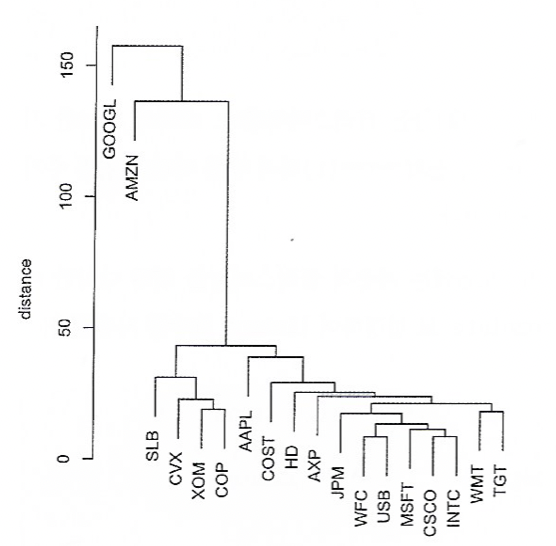
병합 알고리즘

• 계층적 알고리즘에서는 병합이 가장 중요하다.
• 병합 알고리즘의 순서는 다음과 같다.
  • 데이터의 모든 레코드에 대해, 단일 레코드로 이루어진 클러스터를 초기 클러스터로 잡는다.
  • 모든 쌍의 클러스터의 비유사도를 계산한다.
  • 비유사도에 따라 가장 가까운 클러스터를 결합한다.
  • 둘 이상의 클러스터가 남아 있으면 반복하고, 그렇지 않다면 멈춘다.
• 비유사도를 측정하는 방법 중 하나는 완전연결 방법이다.
• 이는 두 클러스터 $A, B$ 사이의 모든 레코드 쌍의 최대 거리를 이용한다(끝과 끝)

비유사도 측정

• 완전연결, 단일연결, 평균연결, 최소분산 등이 있다.

단일연결

• 단일연결은 두 클러스터의 레코드 간 최소 거리를 이용하는 방법이다.
• 이는 Greedy한 방법이며, 결과가 서로 크게 다른 레코드를 포함할 수도 있다.

평균연결

• 모든 거리 쌍의 평균을 사용하는 방법이다. 단일연결과 완전연결의 절충안이다.

최소분산

• 클러스터 내의 제곱합을 최소화한다.

📚 모델 기반 클러스터링

• 기존의 클러스터링 방식은 살짝 휴리스틱한 방법.
• 클러스터의 성질과 수를 결정하는 데 더 엄격한 방법을 쓴다.

다변량정규분포

• $p$개의 변수 집합 $X_1, ...,X_p$의 정규분포를 일반화한 것이다.
• 분포는 평균 집합과 공분산행렬로 정의된다. (공분산행렬은 변수가 서로 어떻게 상호 관련되어 있는지 나타내는 지표)

정규혼합

• 모델 기반 클러스터링의 핵심 개념은 각 레코드가 $k$개의 다변량정규분포 중 하나로부터 발생했다고 가정하는 것이다.
• $k$가 바로 클러스터의 개수이다.

클러스터 개수 결정

• k-평균이나 계층적 클러스터링과 다르게, 모델 기반 클러스터링은 클러스터를 추가하면 할수록 파라미터의 개수도 많아지지면 적합도도 좋아진다.
• BIC 값을 주로 이용하여 엘보우 방법을 시행해서 선택한다.

📚 스케일링과 범주형 변수

• 비지도 학습에서는 데이터를 적절하게 스케일해야 한다.
• 범주형 데이터는 클러스터링 과정에서 문제를 일으킬 수 있다.
• 일반적으로 원-핫 인코딩(0과 1로 이루어진 행렬)을 통해서 이진 변수 집합으로 변환한다.
• 이는 두 가지 값만 가지기 때문에 클러스터링에서 문제가 생길 수 있다.

변수 스케일링

• 단위가 많이 다르면 데이터를 먼저 정규화해야 한다.
  

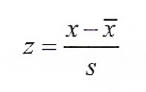
지배 변수

• 변수의 단위가 모두 동일하고 상대적 중요성을 정확하게 반영하는 경우에도 변수의 스케일을 재조정하는 것이 유용할 수 있다.
• 전체 데이터에 영향을 미치는 지배적인 데이터의 경우 스케일링을 통해 요소의 분산을 찾아내는 것.
• 이 지배 변수를 배제하느냐 포함하느냐는 분야에 따라 다르다.

범주형 데이터와 고워 거리

• 데이터를 구성하는 변수들에 연속형과 이진형이 섞여 있으면 스케일링의 기준으로 고워 거리를 이용하는 게 대표적이다.

고워 거리

• 기본적인 개념은 각 변수형 데이터 유형에 따라 지표를 다르게 적용하는 것이다.

  • 수치형이나 범주형 변수에서 두 레코드의 거리는 차이의 절댓값 (맨해튼 거리)로 계산한다.
  • 범주형 변수는 다르면 거리가 1, 같으면 0이다.

계산은 다음과 같다.

• 각 레코드의 변수의 거리를 계산한다.
• 각 거리를 최소 0, 최대 1이 되도록 스케일링한다.
• 거리 행렬을 구하기 위해 스케일된 거리를 모두 더하고 평균 혹은 가중평균을 계산한다.

혼합 데이터의 클러스터링 문제

• 혼합 데이터에서 $z$점수를 사용하면 이진 변수가 너무 큰 영향을 미친다.
• 따라서 혼합된 데이터에서 스케일링을 사용하지 않도록 조심해야 한다.