📚 비지도학습

• 레이블링 과정 없이 데이터를 주고 모델을 훈련하는 과정

📚 주성분분석(PCA)

• 데이터의 차원을 줄이는 데 사용

두 변수 $X_1, X_2$에 대해 두 주성분 $Z_i$가 있다고 하자.

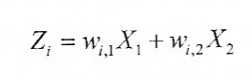
이 때 $w$를 각각 성분의 부하라고 한다.
(원래 변수를 주성분으로 변환할 때 사용한다)
첫 주성분 $Z_1$은 전체 변동성을 가장 잘 설명하는 선형결합이다.
두 번째 주성분 $Z_2$는 $Z_1$과 수직이며 나머지 변동성을 설명한다.
(성분이 더 있다면, 각각은 모두 수직이다.)

주성분은 값 자체보다는 평균으로부터의 편차에 대해 계산하는 것이 일반적이다.

계산과정

• 전체 변동을 최대한 설명하는 선형결합 (위에서와 비슷한 식)을 찾는다.
• 이 선형결합은 첫 번째 새로운 예측변수 $Z_1$이 된다.
• 같은 변수들로 다른 가중치를 가지고 $Z_2$를 만드는 것을 반복한다. 이 때, $Z$끼리는 상관성이 없어야 한다.
• 원래 변수 $X_i$의 개수만큼 $Z_i$를 구할 때까지 반복한다.
• 대부분의 변동을 설명할 수 있는 $Z_i$만 남겨놓는다.
• 각 주성분에 대한 가중치 집합을 얻게 된다.
• 원래 데이터에 이 가중치를 적용해 새로운 주성분으로 변환한다.

주성분 해석

• 스크리그래프 : 주성분의 상대적인 중요도를 표시한다.
  

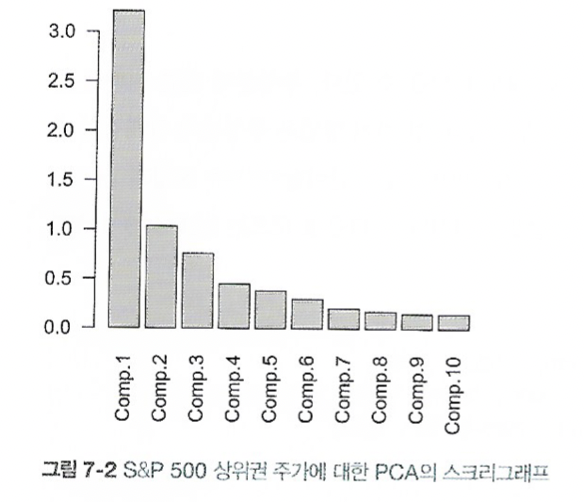
성분을 고르는 데는, 누적 분산의 임계치를 설정하는 방법과 교차타당성검사를 하는 방법이 있다.

📚 대응분석

• PCA는 범주형 데이터에 사용할 수 없다. 따라서 범주형에는 대응분석을 사용한다.
• 범주간 피처 혹은 범주 간의 연관성을 인식한다.
• 저차원 데이터의 그래프 분석에 주로 이용된다. (PCA처럼 전처리에 사용되지는 않는다.)

주 개념