📚 분산분석(ANalysis Of VAriance, ANOVA)
도대체 누가 이걸 ANOVA로 줄일 생각을 했을까?
- A/B 두 그룹 이상의 그룹에 대한 차이를 검정할 때 사용하는 기법
- 다중 검정의 경우 알파 인플레이션이 발생할 수 있는데, 때문에 각각 1회씩 비교하지 않는다.
- 대신 전체적인 부분을 다루는 총괄검정에 속한다.
- 독립변수의 갯수에 따라 일원 분산분석, 이원 분산분석으로 구분한다.
🎮 과정
- 모든 데이터를 취합한다
- 데이터를 섞고 임의로 그룹의 수만큼의 표본을 추출한다
- 각 그룹의 평균을 기록한다
- 네 그룹의 평균 사이의 분산을 기록한다
- 여러 번 반복한다
재표본추출한 분산이 관찰된 변화를 초과한 시간이 p값이 된다.
🎮 예제 : 임의순열을 통한 일원분산분석
데이터는 https://github.com/gedeck/practical-statistics-for-data-scientists/blob/master/data/four_sessions.csv 의 four_sessions를 이용했다.
📊 데이터 가져오기
import pandas as pd
data = pd.read_csv('/content/drive/MyDrive/KHUDA/통계학 스터디/2주차_통계적 실험과 유의성검정/data2.csv')
data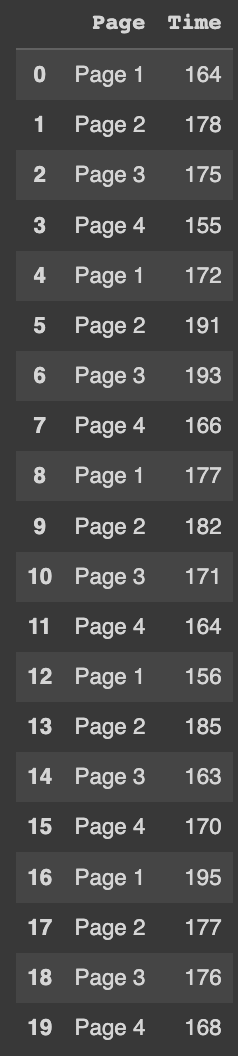
페이지별 머문 시간이 적혀져있다.
📦 Box Plot
import matplotlib.pyplot as plt
data.groupby('Page').boxplot(figsize=(5, 5))
plt.show()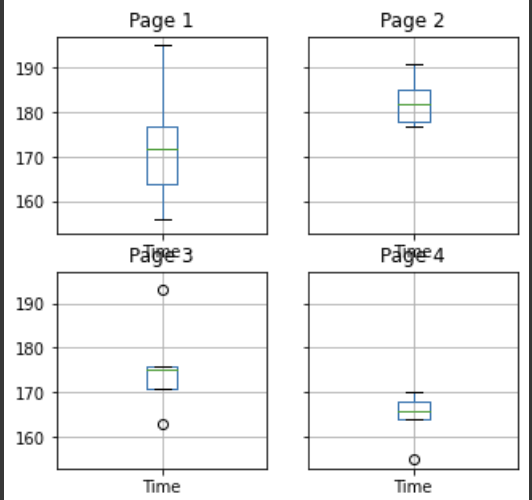
그림으로 보면 꽤나 유의미한 차이가 있지 않을까?
🦎 일원분산분석
# 관측된 분산
observed_var = data.groupby('Page').mean().var()[0]
print('observed means : {}'.format(data.groupby("Page").mean().values.ravel())) #Ravel 1차원으로
print('Variance : {}'.format(observed_var))
import numpy as np
#임의순열로 만든 데이터의 분산을 반환 -> 페이지는 그대로, 값만 다 바꿈
def perm_test(df):
df = df.copy()
df['Time'] = np.random.permutation(df['Time'].values)
return df.groupby('Page').mean().var()[0]
perm_variance = [perm_test(data) for _ in range(3000)]
# p값
print("Prob : {}".format(np.mean([var > observed_var for var in perm_variance])))
약 7.6%로, 유의수준보다 높기 때문에 각 그룹별 머문 시간은 통계적으로 유의미하지 않다.
💨 F 통계량 기반 일원분산분석
F분포와 통계량은 이전 포스팅에서 다루었다.
F 통계량은 그룹 통계량의 비율로 이루어지기에 1에서 멀수록 차이가 크고, 1에 가까울수록 차이가 작다.
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
model = ols("Time ~ Page", data=data).fit()
aov_table = anova_lm(model)
aov_table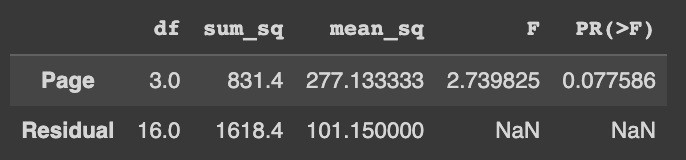
역시 7%가 나온다.
