[통계] 카이제곱검정(chi-squared test)

hyun·2022년 8월 18일

KHUDA 스터디 통계

통계

목록 보기

27/37

χ 카이제곱분포

이전에 카이제곱분포를 다루면서 분포와 검정에 대해 정리한 글이 있다.
[통계] 카이제곱분포 (Chi-Squared Distribution)

간략하게 말하면, 자유도만큼의 샘플을 무작위로 뽑아 모두 제곱해서 더한 통계량의 분포가 카이제곱분포이다.

이는 편차와 오차를 주로 다루고, 표본분산을 보고 모분산을 추측하는 것이 주 목표가 된다.

📊 카이제곱검정

검정 역시 글 상단에 걸어둔 링크에 정리해두었다.

교차검증 시, 변수 간 독립성의 귀무가설이 타당한지 평가하기 위해 관례적으로 $r \times c$ 분할표를 함께 사용한다.
분할표에 대해 통계량의 계산방법은 다음과 같다.
위 식으로 검정통계량을 구하고 카이제곱분포표를 본 후 p값을 구하면 된다.
자유도는 (c-1)(r-1)이 된다.

🎮 실습

🎲 임의순열검정과 검정통계량

📊 데이터 가져오기

실습은 [데이터 분석을 위한 통계] 를 참고했고, 데이터는 https://github.com/gedeck/practical-statistics-for-data-scientists/blob/master/data/click_rates.csv 에서 가져왔다.

from scipy.stats import chi2_contingency
import pandas as pd

data = pd.read_csv('/content/drive/MyDrive/KHUDA/통계학 스터디/2주차_통계적 실험과 유의성검정/click_rate.csv')
data

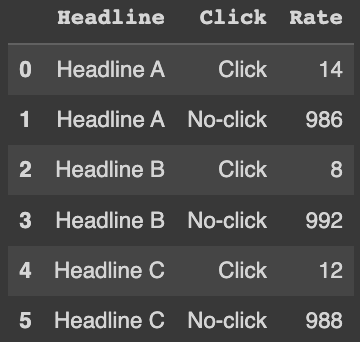
🎲 카이제곱 분할표 꼴로 만들기

data_a = data[data['Headline'] == 'Headline A']
data_b = data[data['Headline'] == 'Headline B']
data_c = data[data['Headline'] == 'Headline C']
df = pd.DataFrame({'A' : [data_a[data_a['Click'] == 'Click']['Rate'].sum(), data_a[data_a['Click'] == 'No-click']['Rate'].sum()],
                   'B' : [data_b[data_b['Click'] == 'Click']['Rate'].sum(), data_b[data_b['Click'] == 'No-click']['Rate'].sum()],
                   'C' : [data_c[data_c['Click'] == 'Click']['Rate'].sum(), data_c[data_c['Click'] == 'No-click']['Rate'].sum()],
})
df.index = ['Click', 'No-click']
df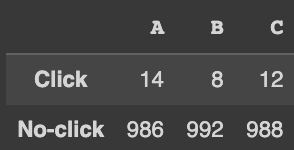

자유도는 (3-1)(2-1)=2이다.

🎲 임의순열검정

import numpy as np
import random

# 재표본추출
box = [1] * 34
box.extend([0] * 2966)

# 1이 클릭, 0이 no클릭 -> 섞기
random.shuffle(box)

# 피어슨 잔차
def chi2(ob, exp):
  pearson_res = []
  for row, expect in zip(ob, exp):
    pearson_res.append([(obs-expect)**2/expect for obs in row])
# 제곱의 합 -> 검정통계량 반환
  return np.sum(pearson_res)

# 귀무가설 구현
expected_clicks = 34/3
expected_noclicks = 1000 -expected_clicks
expected = [expected_clicks, expected_noclicks]

# 검정통계량 계산
chi2_observed = chi2(df.values, expected)

def perm_fun(box):
  sample = [
      sum(random.sample(box, 1000)),
      sum(random.sample(box, 1000)),
      sum(random.sample(box, 1000))
  ]
  sample_noclicks = [1000 - n for n in sample]
  # 순열검정으로 재표본추출 후 검정통계량 계산
  return chi2([sample, sample_noclicks], expected)

perm_chi2 = [perm_fun(box) for _ in range(2000)]

# 재표본추출로부터 얻은 P값, 전체 확률 구하기
resampled_p_val = sum(perm_chi2 > chi2_observed) / len(perm_chi2)
print ("observed chi2 : {}".format(chi2_observed))
print("p-val : {}".format(resampled_p_val))

chi2 검정통계량은 약 1.67, p값은 0.487이 나왔다.
따라서 집단 A,B,C간 차이는 우연으로 발생할 수 있다 == 통계적으로 유의미한 없다 라는 귀무가설을 채택한다.

📊 그려보기

import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(5,5))
ax.hist(perm_chi2)
ax.axvline(x=chi2_observed, lw=2, color='black')
plt.show()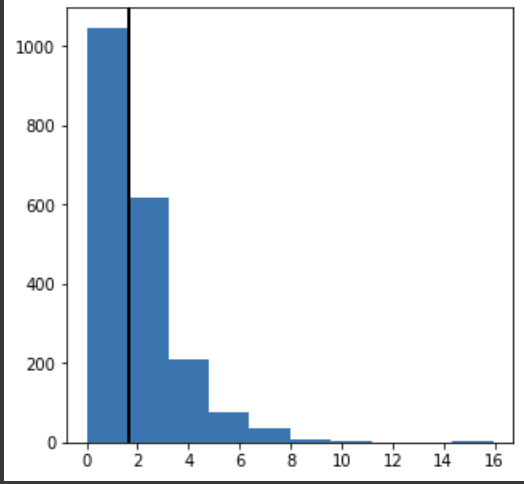

관찰된 결과를 검은 수직선으로 표현했다. 순열검정을 통해 얻은 통계량이 카이제곱분포와 비슷하게 구성되고, 관찰된 결과 또한 순열분포 내에 존재하므로 더 직관적으로 '우연한 발생범위 내' 라는 것을 파악할 수 있다.

🤩 라이브러리를 이용한 카이제곱검정

from scipy.stats import chi2_contingency

chisq, pval, df, expected = chi2_contingency(df)
print('observed chi2 : {}'.format(chisq))
print('p-val : {}'.format(pval))