📚 선형판별분석 (Linear Discriminant Analysis)
-
트리, 로지스틱 회귀 등의 정교한 기법이 발명된 후로 많이 사용되지는 않지만, 주성분분석과 같은 분야에서 아직도 사용된다.
-
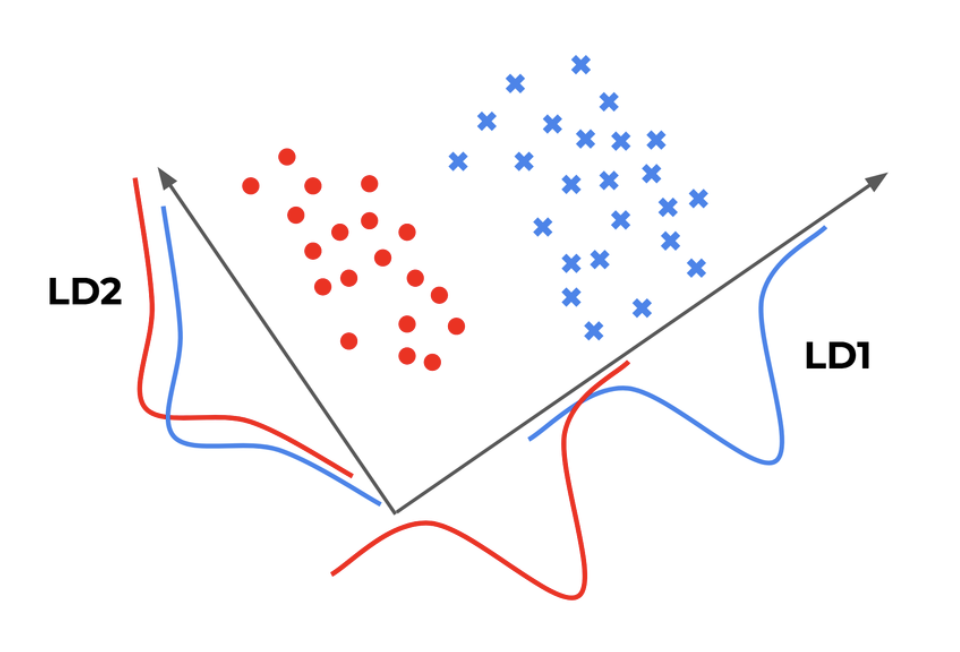
데이터를 어느 한 축에 사영시켜 그룹이 더 잘 구분되는 직선을 찾는 것을 목표로 한다.
아래 이미지에서는 LD2 축보다 LD1 축을 골라 분류하는 것.
공분산
이를 이해하기 위해서 공분산의 개념이 필요하다.
공분산은 두 변수 와 사이의 관계를 의미하는 지표이다. 정의는 다음과 같다.
상관계수가 -1, 1에서 정의되었지만 공분산의 척도는 와 의 척도에 따라 달라진다. 다만 비슷하게, 음수는 음의 관계, 양수는 양의 관계를 표현한다.
와 에 대한 공분산행렬 는 다음과 같이 정의된다.
이는 다변량분석에서 공분산행렬을 통해 마할라노비스 거리를 구하기 위함으로 LDA와 연관이 있다고 한다.
피셔의 선형판별
-
판별분석은 보통 예측변수가 정규분포를 따르는 연속적인 변수라는 가정이 있지만 실제로는 정규분포를 따르지 않거나, 이진 예측변수라도 잘 동작한다.
-
피셔의 선형판별은 그룹 안의 편차와 다른 그룹 간의 편차를 비교한다.
-
더 구체적으로는 레코드를 나누기 위해, 가 최대가 되는 선형결합을 탐색한다.
-
는 두 그룹 평균 사이의 거리의 제곱합, 는 공분산행렬을 통해 가중치를 적용한, 각 그룹 내 평균이 주변에 퍼져 있는 정도의 제곱합이다.
-
직관적으로 봤을 때 그룹의 분산은 작고 그룹 간 차이는 커야 그룹 나누기에 유리하다.
💻 실습
데이터 가져오기
데이터와 실습의 출처는 [데이터 과학을 위한 통계] 책이다.
import pandas as pd
loan_3000 = pd.read_csv('/content/drive/MyDrive/KHUDA/통계학 스터디/5주차_분류/loan_3000.csv')
# category로 바꿔줘야
loan_3000.outcome = loan_3000.outcome.astype('category')
predictors = ['borrower_score', 'payment_inc_ratio']
outcome = 'outcome'
X = loan_3000[predictors]
y = loan_3000[outcome]LDA 사용
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
loan_lda = LinearDiscriminantAnalysis()
loan_lda.fit(X,y)
# scalings_ 선형판별자 가중치
pd.DataFrame(loan_lda.scalings_, index=X.columns)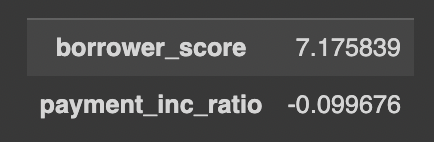
위와 같은 방법으로 판별자의 가중치를 구할 수 있다.
그래프 그려보기
import numpy as np
# 각 축의 그룹의 평균
center = np.mean(loan_lda.means_, axis=0)
# 기울기
slope = - loan_lda.scalings_[0]/loan_lda.scalings_[1]
# y=ax+b에서 b=y-ax
intercept = center[1] - center[0]*slope
# payment_ratio가 0과 20인 지점 찾기
x_0 = (0 - intercept)/slope
x_20 = (20 - intercept)/slope
# loan_3000 데이터에 연체 확률 열 추가
lda_df = pd.concat([loan_3000, pred['default']], axis=1)
import matplotlib.pyplot as plt
import seaborn as sns
fig, ax = plt.subplots(figsize=(4,4))
g = sns.scatterplot(x='borrower_score', y='payment_inc_ratio',
hue='default', data=lda_df, palette=sns.diverging_palette(240, 10, n=9, as_cmap=True),
ax=ax, legend=False
)
ax.set_ylim(0, 20)
ax.set_xlim(0.15, 0.8)
ax.plot((x_0, x_20), (0, 20), linewidth=3)
# 각 그룹에 대한 평균
ax.plot(*loan_lda.means_.transpose())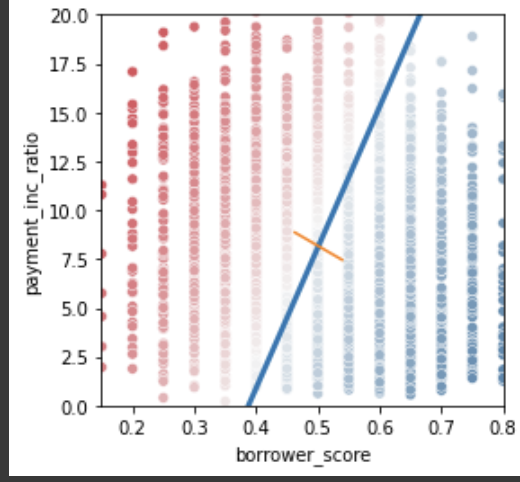
그래프 중앙 직선에서 멀어질수록 신뢰도가 상승한다.
왼쪽 위일수록 연체 확률이 높고 오른쪽 아래일수록 연체 확률이 낮다.
참고
📚 [데이터 분석을 위한 통계]
