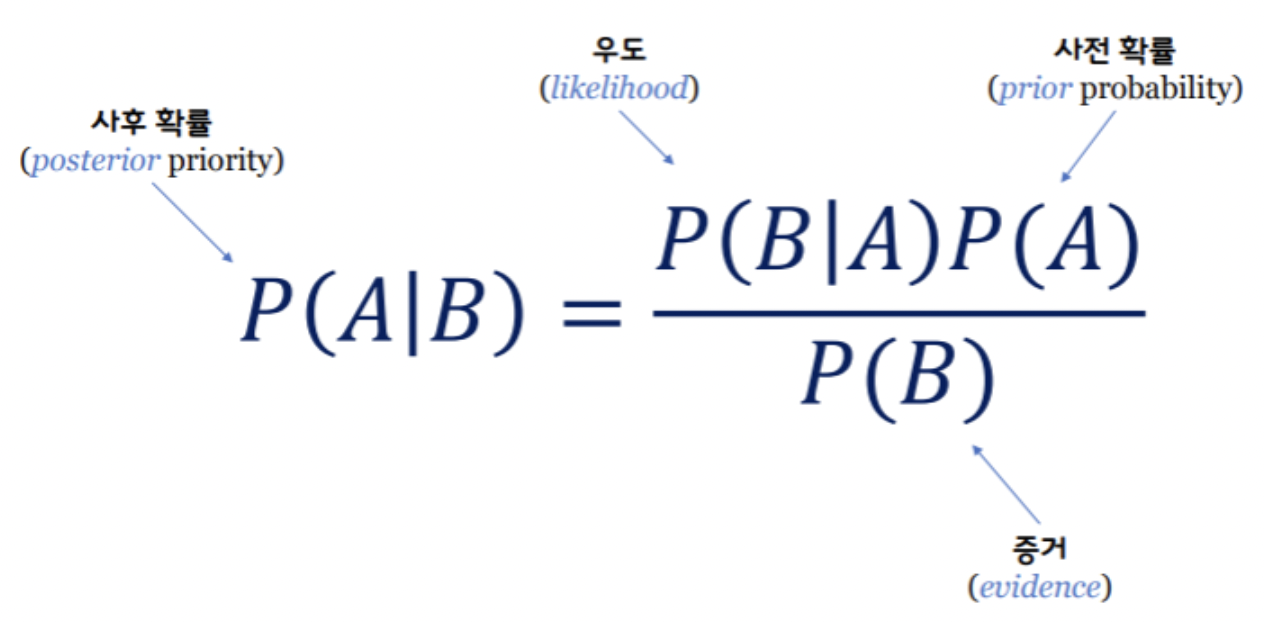
베이즈 정리. 이미지 출처 : 링크

📚 나이브 베이즈 알고리즘

• 분류 알고리즘의 하나로, 주어진 결과에 대해 예측변숫값을 관찰할 확률로 예측변수 -> 결과를 예측하는 알고리즘이다.

• 영단어 Naive의 뜻은 "순진한, 단순한, 천진난만한" 등의 뜻이 있다. 이는 원래 베이즈 분류가 빡빡하게
  "모든 예측변수가 동일한 레코드를 찾고, 그 클래스들로 예측값을 만들기 때문에"
  너무 strict하지 않은 방법이 필요했다. 현실에서는 데이터의 파라미터가 모두 동일할 리가 없으니!
  후술하겠지만, 이를 단순한 조건부확률의 곱으로 구할 수 있다고 가정하기에 '나이브하다' 고 표현된다.

  ---

  🚨 나이브 베이즈 알고리즘의 예측변수는 범주형이어야 한다. 수치형이라면 범주형으로 바꿔주거나 조건부 확률을 구할 때 정규분포를 이용하는 방법밖에 없다.

  ---

• 나이브 베이즈로 분류하는 과정은 다음과 같다.

- 이진 응답 $Y=i$(i=0,1)에 대해 각 예측변수에 대한 조건부확률 $P[X_j | Y=i]$을 구한다.	
이는 $Y=i$인 모든 아웃풋 중 $X_j$가 등장한 비율로 구할 수 있다.

- 각 확률값을 곱하고, $Y=i$에 속한 레코드들의 비율을 곱한다. 
(이는 $P[X_j | Y=i]P[Y=i]$이므로 베이즈 정리의 분자에 해당한다.)

- 모든 클래스에 대해 반복한다.

- 2번에서 구한 확률값을 모두 더하면 가능한 $X_j$의 확률공간이 되기 때문에 클래스 $Y=i$에 대한 확률을 확률값의 합으로 나눠준다.

• 개인적으로는 식으로 보는 것이 더 편했다.
  $P[Y=i|X_1,...X_p] =\frac{P[X_1,...,X_p|Y=i]P[Y=i]}{P[X_1, ..., X_p]}$
  \
  $=\frac{P[Y=i]P[X_1|Y=i]...\times P[Y=i]P[X_p|Y=i]}{P[Y=0]P[X_1|Y=0]...P[X_p|Y=0]+P[Y=1]P[X_1]...P[X_p]}$

다만 여러 확률값을 곱으로 나타낼 때 필요한 전제가 있는데, 그것은 각 확률변수들이 독립이라고 가정해야 하는 것. 즉 $i\neq k$인 $X_i, X_k$는 독립이어야 한다는 점이다.

나이브 베이즈에서는 이를 가정하고 시작한다. 그로부터 이름의 '나이브함'이 붙은 것.

🚨 나이브 베이즈는 편향된 값을 많이 예측한다고 한다. 그러나 카테고리별 예측 순위가 필요한 것이라면 괜춘 !

---

💻 실습

데이터 : 링크

실습과 데이터는 [데이터 과학을 위한 통계] 책을 참고하였다.

데이터 읽어오기

import pandas as pd

loan_data = pd.read_csv('/content/drive/MyDrive/KHUDA/통계학 스터디/5주차_분류/loan_data.csv')
loan_data.head()
predictors = ['purpose_', 'home_', 'emp_len_']
outcome = 'outcome'

X = pd.get_dummies(loan_data[predictors], prefix='', prefix_sep='')
y = loan_data[outcome]

Naive-Bayes 사용하기

from sklearn.naive_bayes의 MultinomialNB 클래스로 이용할 수 있다.

from sklearn.naive_bayes import MultinomialNB
# alpha는 모델의 복잡도 결정(반비례)
# fit_prior는 각 클래스 확률을 사용하는지 - 안하면 균등분포 사용
naive_model = MultinomialNB(alpha=0.01, fit_prior=True)
naive_model.fit(X, y)

# 마지막 값으로 테스트
new_loan = X.loc[146:146, :]
# 연체 예상
print('predicted class : {}'.format(naive_model.predict(new_loan))) 

마지막 레이블에 대해 값을 '연체' 라고 예측한 것을 볼 수 있다.

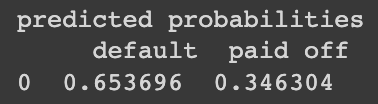
각 클래스에 대한 사후확률도 체크할 수 있다.

probs = pd.DataFrame(naive_model.predict_proba(new_loan), columns=loan_data[outcome].astype('category').cat.categories)
print('predicted probabilities\n', probs)