[통계] 선형회귀

hyun·2022년 8월 22일

통계

목록 보기

30/37

0. 선형회귀란?

변수 X와 Y의 관계를 정의하고, 그로부터 새로운 X에 대한 Y값을 예측하는 모델을 훈련하는 과정.
이는 문제-답이 주어져야 하는 지도 학습 (supervised learning)에 속한다.
또 데이터 과학과 통계학 사이의 중요 연결 고리는 이상 검출 영역인데, 회귀 분석은 데이터 분석을 위해 개발되었지만 발전과 함께 데이터의 이상치를 검출하는 데도 사용되고 있다.

📚 단순선형회귀

한 변수와 또 다른 변수의 크기 사이의 관계에 대한 모델이다.
X가 커질 때 Y가 어떻게 변화하는지 밝히는 과정이라 할까?

이는 상관관계의 개념과도 비슷한데, 상관관계가 두 변수 사이 전체적인 관련도를 측정하는 것이라면, 회귀는 관계 자체를 정량화하는 방법이라는 차이가 있다.

🛩 회귀식

회귀에서는 아래와 같은 선형 관계식을 통해 X로부터 Y를 예측하는 것이 그 목표이다.

Y = aX + b

직선의 방정식과 그 궤를 같이 하기 때문에, $a$ 를 기울기 혹은 계수(coefficient) 라고 하고, $b$ 를 절편 이라고 한다.

💡 적합값과 잔차

데이터가 일직선상에 예쁘게 올라온다는 것은 사실상 불가능하다. 따라서 회귀식은 오차항을 포함할 수밖에 없다.
실제 데이터값의 식은 오차 $e_i$ 만큼 떨어져 있게 될 것이므로 이렇게 될 것이다.

Y = aX_i+b+e_i

이는 오차를 포함한 값으로, 적합값, 즉 나와야 하는 값은 오차 없이

\hat{Y}=aX_i+b

가 된다.

이 때 잔차인 $e_i$ 는 $\hat{Y} - Y$ 를 통해서 구할 수 있다.
따라서 직선과 특정 값의 오차를 잔차라고 하고, 이는 예측값-적합값을 통해 구하는 것.

🤩 최소제곱 (잔차제곱합 RSS)

데이터를 피팅한 모델을 만들기 위해서 잡는 기준이 뭘까?
대표적으로 잔차제곱합(residual sum of squares, RSS) 을 사용할 수 있다.

RSS=\sum_{i=1}^n(Y_i-\hat{Y}_i)^2

회귀선을 만들 때, 이 RSS가 최소가 되는 선을 찾게 된다.
이를 최소제곱회귀 혹은 보통최소제곱(ordinary least squars, OLS)라고 한다.

계산이 굉장히 쉬워서 많이 쓰인다고 !

🤓 다중선형회귀

예측변수가 많은 선형 회귀를 말한다.
예를 들어 변수가 $X_0$ 부터 $X_n$ 까지 있다면 회귀식은

Y=a_0X_0 + a_1X_1 + ... + a_nX_n

이 된다.
이 직선을 찾아내는 모델을 다중선형회귀 라고 한다.

⭐️ 모형 평가

😾 제곱근평균오차 (RMSE)

데이터 과학의 관점에서 가장 중요한 성능 지표는 제곱근평균오차(RMSE)이다.

RMSE=\sqrt{\frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{n}}

이는 예측된 값들의 제곱오차의 평균의 제곱근 (...) 으로 정의된다.
전반적인 모델의 정확도를 측정하고 다른 모델과 비교하기 위한 기준이 된다.

📚 잔차표준오차(RSE)

이외에도 RMSE와 유사한 잔차 표준오차(RSE)가 있는데, 예측변수가 $p$ 개일 때 RSE는 다음과 같다.

RSE = \sqrt{\frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{n-p-1}}

둘의 차이점은 분모가 데이터의 수냐, 자유도냐 인데, 데이터의 크기가 커질수록 둘 다 거기서 거기라고.

💨 결정계수 (R2 통계량)

R제곱 통계량은 0~1 사이의 값으로 모델 데이터의 변동성을 측정한다.
모델이 데이터에 얼마나 적합한지 평가하고자 할 때 사용되고 다음처럼 정의된다.

R^2=1-\frac{ \sum_{i=1}^n(y_i-\hat{y}_i)^2 }{ \sum_{i=1}^n(y_i-\bar{y}_i)^2 }

분모는 y의 분산과 관련있으므로 이는 예측가능변동/총변동 이므로, 직관적인 느낌으로는 총 데이터에서 우리 모델이 설명할 수 있는 비율라고 보면 될 것 같다.
그렇기에 높은만큼 좋겠지 ??

✌️ 교차타당성검사

$R^2$ , t통계량, p값 등은 모두 표본 내 지표들이다. 따라서 좋은 예측을 위해서는 많은 표본이 있어야 되는데, 데이터의 일부를 떼어내는 방식인 홀드아웃 샘플을 여러 개 만들어서 교차검증하는 것을 교차타당성검사라고 한다.

일반적인 k-다중 교차타아성검사 알고리즘은 다음과 같다.

1/k개의 데이터를 홀드아웃 샘플로 따로 빼둔다.
남은 데이터로 모델을 훈련시킨다.
모델일 빼둔 홀드아웃 샘플에 적용시켜 모델 평가 지표를 기록한다.
홀드아웃 샘플을 다시 섞고 다음 데이터로 홀드아웃 샘플을 만들어 빼둔다.
모든 데이터가 홀드아웃 샘플로 사용될 때까지 반복한다.
평가 지표들을 평균 따위로 결합한다.

이 때 데이터를 나누는 것을 폴드라고 한다.

🦎 모형 선택 및 단계적 회귀

오컴의 면도날 이라는 원리가 있다. 모든 것이 동일한 조건에선, 복잡하기보다는 단순한 모델을 우선 사용해야 한다는 개념이다.

선형 회귀도 동일하다. 학습할 때, 변수가 많아지면 학습 데이터의 정보를 더 알아내기 때문에 RSE는 감소하고 R2는 증가한다. 그러나 이는 과대적합으로 이어질 수 있다.

따라서 모델의 복잡성을 함께 고려하기 위해 다음과 같은 방법들을 사용한다.

수정 R제곱

R^2_{adj}=1-(1-R^2)\frac{n-1}{n-P-1}

$n$ 은 레코드의 수, $P$ 는 모델의 변수의 수를 의미한다.

AIC (변수추가 불이익)

AIC=2P+nlog(RSS/n)

변수가 많아질수록 점수는 높아지기에 불이익을 받게 된다.

단순한 모델을 만들기 위해 부분집합회귀로 가능한 모든 모델을 탐색할 수 있다. 다만 이는 비용이 많이 투입되므로,
단계적 회귀를 통해 적절한 모델을 탐색하면 학습을 멈추는 방법을 선호한다.
이는 변수들을 연속적으로 추가하거나 삭제해서 최적의 모델을 찾는 방법인데, 변수를 삭제해 나가는 것을 후진제거, 변수를 추가하면서 나아가는 것을 전진선택이라고 한다.

🏋️‍♂️ 가중회귀

각 요소에 가중치를 다르게 두어 그 요인이 회귀분석 값에 미치는 영향을 조절한다.
간단함 ! 실습에서 보자.

📊 회귀를 이용한 예측

회귀는 주어진 데이터에 대해서 예측을 수행하기 때문에, 주어지지 않은 부분을 예측하는 데에는 무리가 있다.

같은 맥락에서 회귀를 했을 때 중요한 것은 모델이 예측한 y값의 구간 이다.
이를 예측구간이라고 한다.

? 신뢰구간과 예측구간의 차이점

"예측한 결과에 대한 신뢰구간" 이라고 예측구간을 이해할 수 있다.

순열분포로 생각한다면, 예측값으로 히스토그램을 그릴 수 있다.
그리고 개별 값에 대해 그 값이 우연에 의해 발생할 수 있는 정도인지 선택할 수 있다는 것.

📊 회귀에서의 요인변수

범주형 변수 (명명척도)

범주형 변수는 요인변수라고도 불리는데, 개수가 제한된 이산값을 취하는 변수를 말한다.
지표변수는 예/아니오 등 이진 변수를 가지는 경우이다.

회귀분석은 수치 입력이 필요하므로 이를 수치형으로 바꿔 입력해줘야 한다.

가장 일반적으로는 변수를 이진 가변수들의 집합으로 변환하는 것.

가변수 표현

범주를 숫자로 바꿔주는 과정을 나타낸다.

사진과 같은 범주를 가지는 데이터가 있다고 하자.

그러면 원-핫 인코딩 이라 불리는 방법을 통해서 아래와 같은 행렬로 변환할 수 있다.

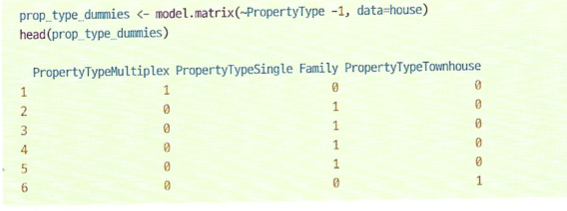
1행은 Multiplex를 가지므로 해당 열만 1, 2~4행은 single falmily, 마지막 행은 townhouse이기 때문데 위와 같은 행렬로 변환된다.

파이썬에서는 pandas의 get_dummies를 이용해서 범주형 변수를 더미로 변환할 수 있다.
🚨 이 때 반환되는 열은 P-1이다. 다중공선성 때문에 나머지가 모두 아니면 어차피 정해지기 때문!

! 범주형 데이터의 범주가 너무 많으면 모든 요소를 유지할지 아니면 수준을 통합할지 결정해야 한다.

순서가 있는 요인변수 (서열척도)

어떤 요인변수는 순서가 있는데, 이는 일반적으로 바로 숫자로 바꿔서 사용해도 된다.

📚 회귀방정식의 상관 문제

회귀에 사용되는 변수들이 상관이 있을 시, 회귀계수의 값이나 의미를 해석하기 어려워질 수 있다. 따라서 상관이 있는 변수들은 사용하지 않는 것이 좋다.

📚 다중공선성

-> 예측변수가 다른 변수들의 선형결합으로 표횐다는 것.

한 변수가 여러 번 포함되거나,
요인변수를 가변수 표현할 때 P-1개가 아닌 P개의 가변수가 만들어지거나,
두 변수가 굉장히 높은 상관성이 있을 경우
발생한다.
회귀분석에서는 굉장히 치명적인 문제라고 한다. 이게 사라질 때까지 변수를 정리해줘야 함.
특정 유형의 다중공선성 문제는 자동으로 처리하지만, 불완전한 다중공선성의 경우 걸러지지도 않고 불안정한 결과를 줄 수도 있다.

📦 교란변수

변수 상관과 대비되게, 교란변수는 회귀분석에 중요한 변수가 포함되지 못해서 생기는 문제이다.
예를 들어 주택 가격을 예측하는 모델링을 한다고 하자. 이 때 위치에 대한 정보가 포함되지 않는다면, 제대로 된 예측은 나오지 않을 것이다.

이런 경우 '실제로는 유의미한 변수인 위치가 반영되지 않아 모델에 교란을 일으키므로' 위치 데이터가 교란변수가 될 수 있다.

📊 상호작용과 주효과

변수 간 상관이 있을 때, 주효과(독립변수)와 그 상호작용을 구분할 수 있다.
R에서 집값과 변수들 사이의 상관을 고려하여 모델링하면 다음과 같은 결과가 도출된다.

ZipGroup0이 제일 가난한 동네라고 할 때, 하단 4개의 변수들을 보면 SqFtTotLiving : 그룹 형식으로 되어 있다.
따라서 지역마다 평수에 따른 결과값이 다르다는 뜻.

📊 특잇값

측정치에서 멀리 벗어난 값.
회귀에서는 실제 y값에서 멀리 떨어져있는 경우이다.
잔차를 표준오차로 나눈 값을 표준화잔차라고 하는데, 이로부터 특잇값을 발견할 수 있다.

표준오차를 알 때, 표준화잔차가 지나치게 크면 (경험적으로 3 이상이면) 그것을 특잇값으로 생각한다고 한다.

📐 영향값

모델에서 제외되었을 때 모델에 중요한 변화를 가져오는 값을 주영향관측값이라고 한다.

잔차가 크다고 반드시 주영향관측값인 것은 아니다.

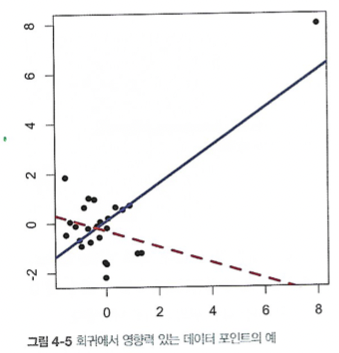
위 그림에서는 실선이 우측 상단의 값을 포함한 것, 점선이 포함하지 않은 회귀식이다.
해당 데이터는 회귀 결과에 큰 영향을 끼치지만, 원래 회귀에서 큰 특잇값으로 나타나지는 않았다.

이 때 저 데이터가 회귀식에 미치는 영향을 레버리지라고 한다.

햇 값 (hat value)

\frac{2(P+1)}{n}

위 식 이상의 값들은 레버리지가 높다고 판단한다.

쿡의 거리 (Cook's distance)

값이

\frac{4}{(n-P-1)}

보다 크면 영향력이 높다고 본다.

이분산성, 비정규성, 오차 간 상관

오차가 정규분포를 따른다면 모델이 완전하다는 신호.
따르지 않는다면 모델에서 뭔가가 누락되었을 수 있음.

추론이 완전히 유효하려면 잔차는 다음 세 조건을 만족해야 한다.

동일한 분산을 가짐 (등분산성)
정규분포를 따름 (정규성)
서로 독립이어야 함 (독립성)

이분산성

이분산성은 데이터 시각화를 통해 비교적 쉽게 유추할 수 있다.
잔차와 예측값을 시각화하면 오차의 분산이 어느 정도인지 판별할 수 있다.

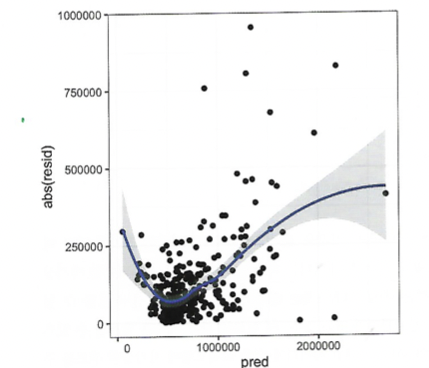
위 그림에서는 가격이 높거나 낮은 구간에서 잔차의 분산이 크다는 것을 알 수 있다.
따라서 모델이 이분산성 오차를 가지고 있고, 모델이 가격이 너무 높거나 낮은 구간에서는 예측 신뢰성이 떨어진다는 사실을 말할 수 있다.

정규성

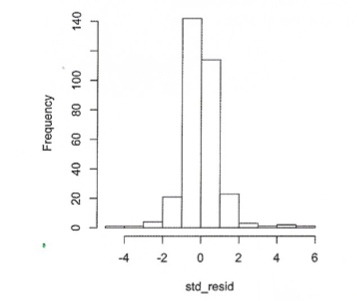
표준화잔차에 대한 히스토그램이 위와 같이 나왔다면, 오차가 정규성을 지니고 있지 않다는 뜻이다.

독립성

시계열 분석을 할 때는 오차가 독립적이어야 한다.
시계열 회귀분석에서 유의미한 자기상관이 있는지 탐지할 때는 더빈-왓슨 통계량을 이용할 수 있다.
회귀모형의 오차 간에 상관관계가 있다면, 이 정보는 단기 예측에 유용하고,
반대로 장기적인 예측 모델을 위해서는 상관관계가 낮아야 한다.

-> 근데 데이터 분석가는 예측이 먼저이므로 여기 목매지 않기 !

😱 편잔차그림과 비선형성

편잔차그림

편잔차그림은 예측변수 하나와 결과에 대한 그래프를 그려보는 것이다.
편잔차 = 잔차 + $a_iX_i$ 로 나타낸다.
그렇게 구한 편잔차의 분포, 그 위에 평활곡선과 회귀선을 그리면 다음과 같다.

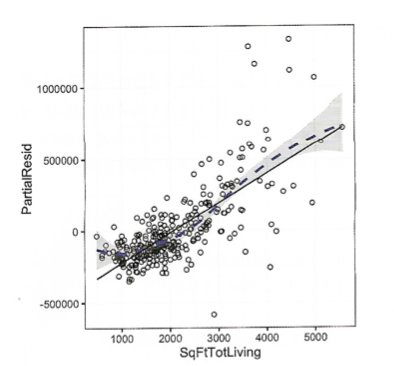
이렇게 보면 sqfttotliving 변수가 집값에 얼마나 영향을 미치는지 볼 수 있다.
회귀선에 따르면, 모델은 작은 집들에 대해서는 가격을 원래보다 낮게, 큰 집에 대해서는 더 높게 예측한다.
따라서 해당 변수는 비선형 항을 고려해볼 수 있다.

😾 다항회귀와 스플라인 회귀

다항 회귀

Y = a_1X_1^2 + a_2X_2+b

식의 다항식을 찾는 회귀분석법이다.
파이썬에서 statsmodels의 ols 모듈을 이용해서 해볼 수 있다.

스플라인

다항 회귀는 딱딱한 직선형 회귀분석에서 벗어날 수 있지만, 고차 항을 많이 추가하는 것은 가끔 회귀식에 문제를 초래한다.
비선형 모델을 모델링하는 더 나은 방법은 스플라인이다.
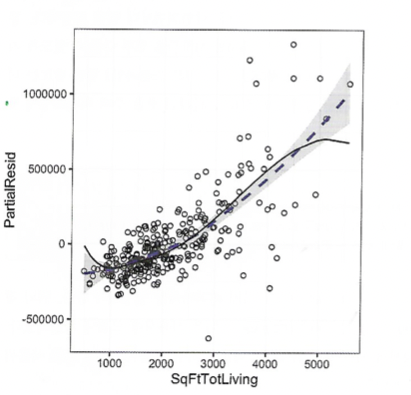
이는 구간 별 다항함수를 구하면서 점과 점 사이를 잇는다.

그래서 그 점을 우리가 잡아줘야 한다 ㅠㅜ

파이썬에서는 역시 statsmodels의 formula 옵션을 통해서 그릴 수 있다.
df - degree만큼 데이터의 분위를 나눠서 매듭을 짓는다.

📊 일반화가법 (GAM)

스플라인 항에 대한 최적의 매듭 점을 자동으로 찾도록 하는 기법.

😵‍💫 단순선형회귀 실습

노동자들이 면진에 노출된 연수와 폐활량의 관계를 선형회귀 모델로 구현해보자.

x = data['Exposure']
y = data['PEFR']

import matplotlib.pyplot as plt

plt.scatter(x, y)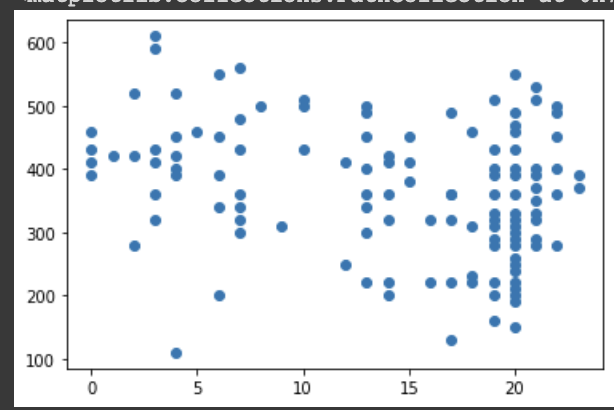

x축이 면진에 노출된 연수, y축이 폐활량이다.
이렇게 봤을 때는 두 변수 간 관계를 직관적으로 파악하기 어렵다.
따라서 scikitlearn을 이용해서 선형회귀를 구현해보자.

🎣 계수와 절편 구하기

x = ['Exposure']
y = 'PEFR'
print(data[x])

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(data[x], data[y])

print('Intercept : {}'.format(lr.intercept_))
print('Coefficient Exposure : {}'.format(lr.coef_[0]))

계수가 -4.184, 절편이 424인 직선의 방정식이 도출되었다.
따라서 노동자가 1년 면진에 노출될 때마다 폐활량은 -4씩 줄어드는 셈.
이렇게 선형 회귀를 통해 변수 간의 상관관계를 정량화할 수 있다.

🚨 잔차 구하기

scores = lr.predict(data[x])
errors = data[y] - scores
linear = [-4.184, 424]

plt.plot(range(30), [ linear[0]*x + linear[1]  for x in range(30) ])
plt.scatter(data[x], data[y], color='r')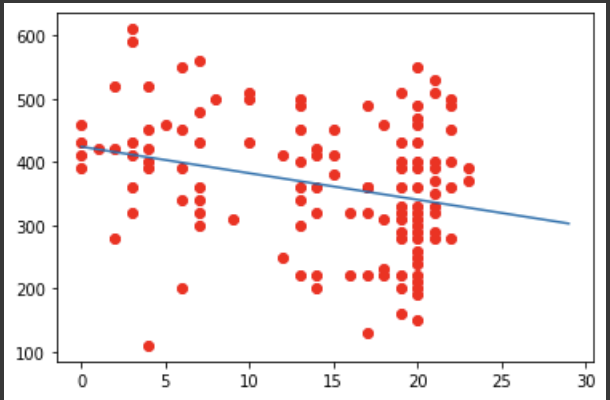

각 점 - 직선 값이 잔차가 된다.

🛩 다중선형회귀 실습

😊 다중선형회귀

위 예제와 동일하게 LinearRegression 클래스로 다중선형회귀를 수행할 수 있다.
데이터는 https://github.com/gedeck/practical-statistics-for-data-scientists/blob/master/data/house_sales.csv

input = house[['SqFtTotLiving', 'SqFtLot', 'Bathrooms', 'Bedrooms', 'BldgGrade']]
output= house[['AdjSalePrice']]

from sklearn.linear_model import LinearRegression
lm = LinearRegression()
lm.fit(input, output)

print("Intercept : {}".format(round(lm.intercept_[0], 3)))
print("Coefficients: {}".format(lm.coef_))

많은 변수에 대해서도 동일하게 Intercept와 coef가 출력되는 것을 볼 수 있다.
이 경우, 각 기울기는 변수 순서대로 된다.
따라서 집값에 가장 영향을 많이 미치는 요인은 집의 크기이다.

😱 모형 평가

sklearn의 mean_squared_error와 r2_score를 이용해서 RMSE와 R2 점수를 구해보자.

from sklearn.metrics import mean_squared_error, r2_score
import numpy as np
 
fitted = lm.predict(input)
RMSE = np.sqrt(mean_squared_error(output, fitted))
r2 = r2_score(output, fitted)

print("RMSE : {}".format(RMSE))
print("R2 : {}".format(r2))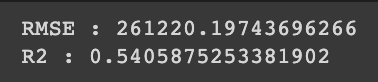

💡 가중회귀 실습

# 가중회귀
house['year'] = [int(date.split('-')[0]) for date in house.DocumentDate]
house['Weight'] = house.year - 2005

input = house[['SqFtTotLiving', 'SqFtLot', 'Bathrooms', 'Bedrooms', 'BldgGrade']]
output = house[['AdjSalePrice']]

lr_wt = LinearRegression()
lr = LinearRegression()

# samlple_weight 옵션으로 가중치 허용
lr_wt.fit(input, output, sample_weight=house.Weight)
lr.fit(input, output)

print('none')
print(lr.intercept_)
print(lr.coef_)
print('-' * 30)
print("weight")
print(lr_wt.intercept_)
print(lr_wt.coef_)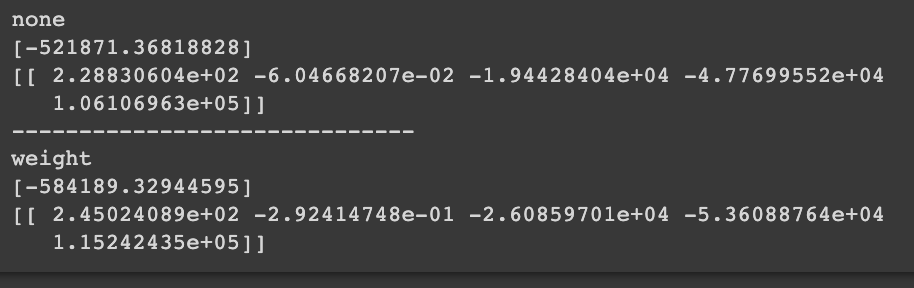

가중치를 허용했을 때 회귀식이 달라지는 것을 확인할 수 있다.

참고 및 출처
[데이터 과학을 위한 통계(2판): 데이터 분석에서 머신러닝까지 파이썬과 R로 살펴보는 50가지 핵심 개념]

hyun

이전 포스트

[통계] 검정력, 효과크기와 표본크기

다음 포스트