[통계] 이항분포

hyun·2022년 8월 13일

통계

목록 보기

13/37

💡 About 이항분포

이항분포란 각 시행마다 성공 확률이 정해져 있을 때, 주어진 시행 횟수에서 성공한 횟수의 도수분포를 뜻한다.
가장 유명한 예시로 동전 던지기가 있는데, 각각의 회차마다 성공 : 실패 확률이 5:5로 정해져 있기 때문.
이 때 $n$ 번의 회차에서 $k$ 번 성공할 확률을 이항 분포라고 한다.
( $n$ =1이면 그냥 베르누이 분포가 된다)

시행 횟수 $n$ 이 충분히 크다면 정규분포에 가까워진다.

📚 공식

$P[X]=_n\mathrm{C_k}p^k(1-p)^{n-k}$ .
$n$ 은 총 시행 횟수, $k$ 는 성공 횟수, $p$ 는 성공 확률이 된다.
비교적 직관적으로 이해할 수 있는데, $n$ 번 시행으로 만들 수 있는 모든 결과에서 $k$ 번 성공할 경우의 수를 구하면 된다. 그럼 각 케이스에 각 경우에 대한 확률을 곱해주면 됨.

📚 성질

📚 이항분포의 평균

$E[X] = np$
증명보다 우선, 상식적으로 생각해본다면 $n$ 번의 시행 후 기댓값은 당연히 전체 시행 횟수 X 성공 확률일 것.
증명은 기댓값의 선형성을 이용한다.
$E[K] = E[K_1 + K_2...+K_n]=E[K_1]+E[K_2]...+E[K_n]$
매회 시행 시 기댓값은 $p$ 와 같으므로 이는 $np$ 로 수렴한다.

📚 이항분포의 분산

$Var[K] = np(1-p)$
각각의 시행에 대해서 보면, 이산확률변수의 분산의 정의에 따라 $Var[X]=\sum p(x_i)(x_i-\mu)^2$ 이다.
따라서 한 시행의 분산은 $(1-p)(0-p)^2 + p(1-p)^2=p^2(1-p)+p(1-p)^2\\=p^2-p^3+p(1-2p+p^2)=p^2-2p^2+p\\=p(1-p)$

따라서 분산의 선형성에 따라서
$Var[K]=np(1-p)$ 가 된다.

📚 실습

📚 p에 따른 이항분포의 변화



fig, axes = plt.subplots(3, 1, figsize=(12, 14))
plt.subplots_adjust(hspace=0.25)
plt.setp(axes, xticks=range(0, 18))

n, p = 15, 0.3
x = np.arange(0, 18)
axes[0].set_title('n=15, p=0.3')
axes[0].bar(x, sp.stats.binom.pmf(x, n, p))

n, p = 15, 0.5
axes[1].set_title('n=15, p=0.5')
axes[1].bar(x, sp.stats.binom.pmf(x, n, p))

n, p = 15, 0.7
axes[2].set_title('n=15, p=0.7')
axes[2].bar(x, sp.stats.binom.pmf(x, n, p))

plt.show()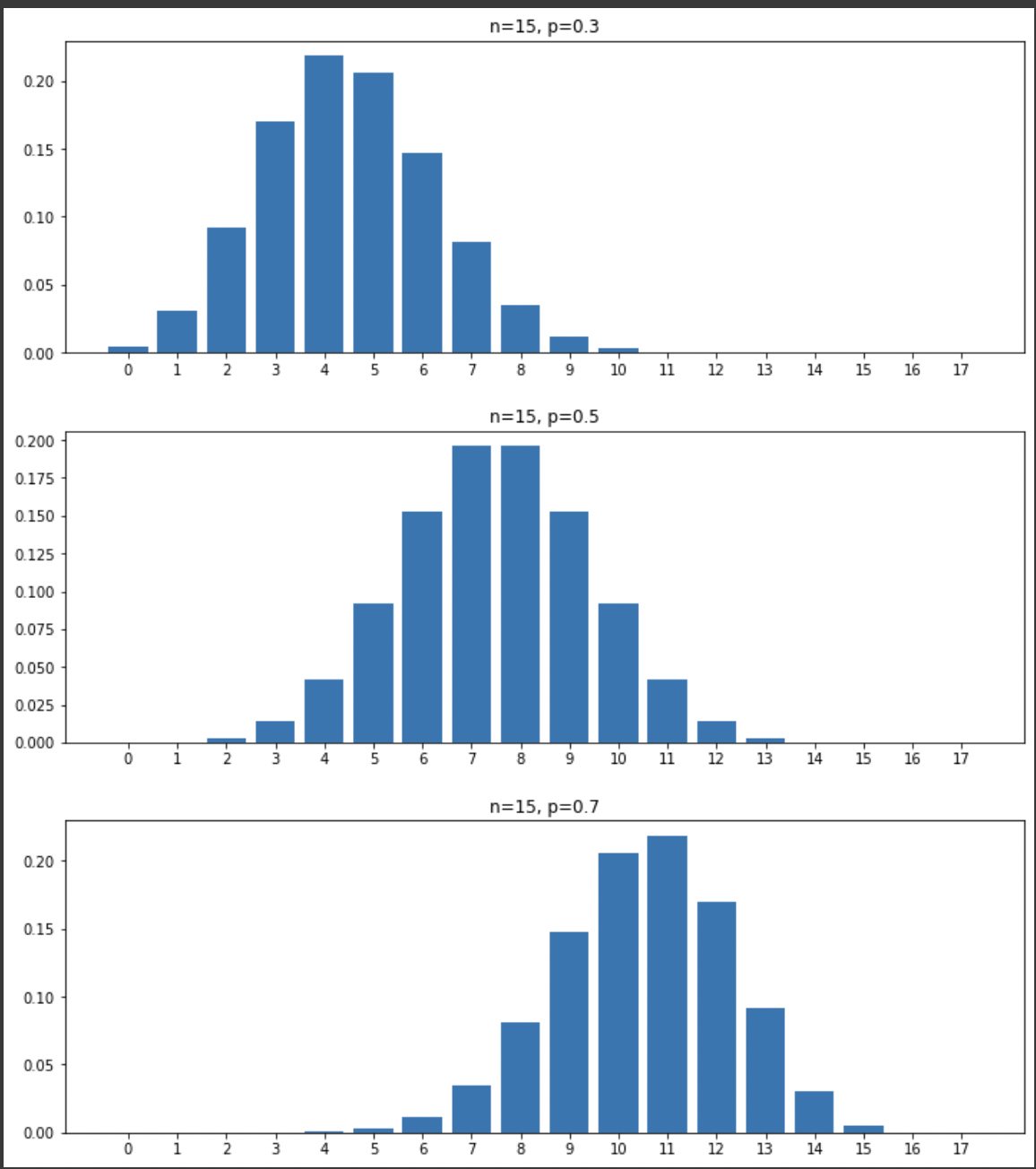

성공 확률에 따라 평균의 값이 바뀌기 때문에 그래프의 중심이 $np$ 에 맞게 옮겨가는 것을 볼 수 있다.

📚 n에 따른 이항분포의 변화

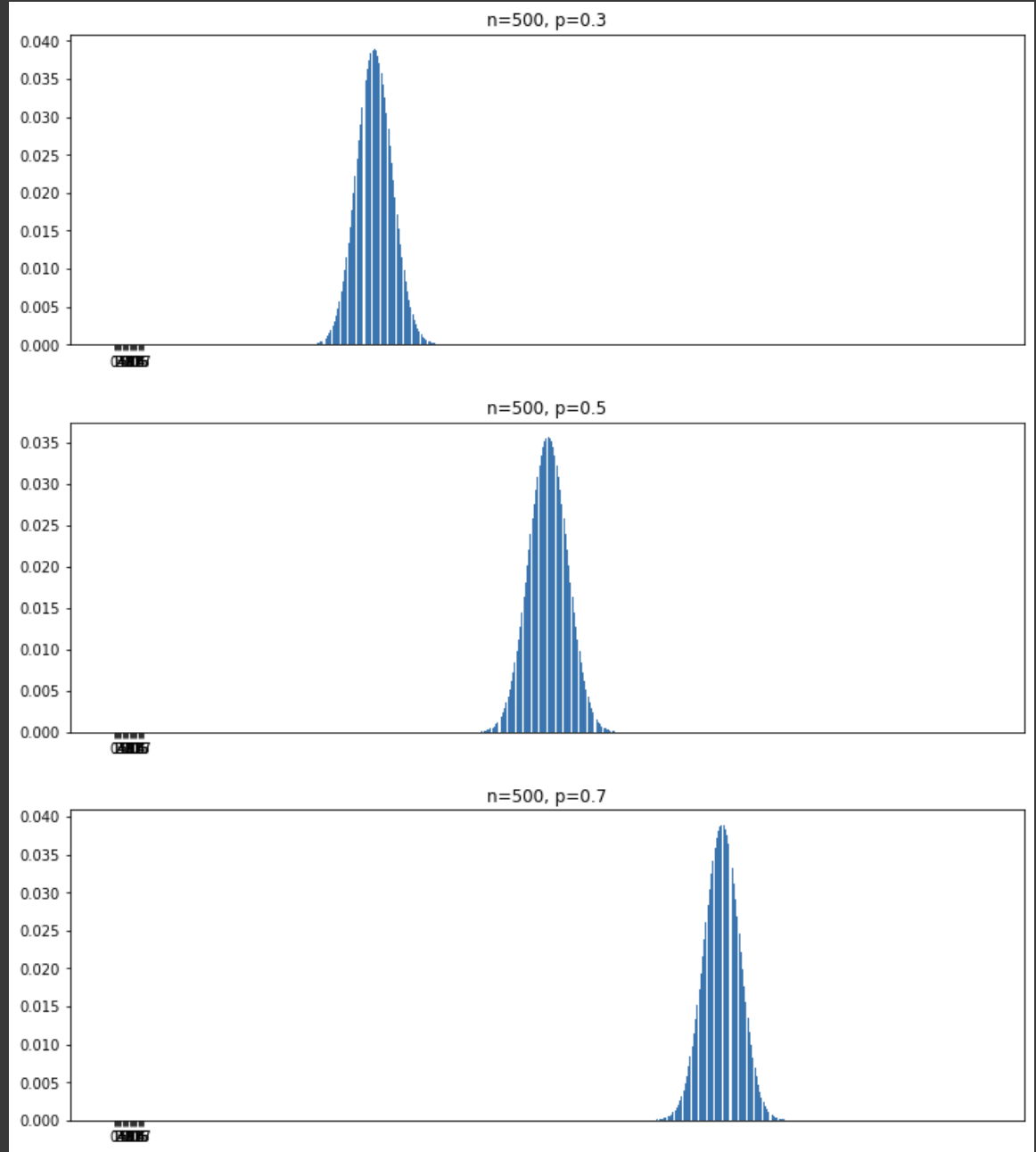
위와 똑같은 코드에서 n의 크기를 늘리면 그래프가 정규분포와 비슷하게 형성되는 것을 볼 수 있따.

📚 연속성 수정 (Continuity Correction)

이항분포는 이산형이고 정규분포는 연속형 확률변수이기 때문에 이산적으로 주어진 구간을 정규분포에 맞도록 바꿔줘야 한다.
이 조정 행위를 💡 연속성 수정이라고 한다.
일반적으로 이를 위해서는 범위에 0.5를 더하거나 뺀다.

📚 예제

Q. 연속성 수정을 고려한 이항분포의 정규분포 근사

대학생 중 20%는 밖에 나가기 싫고 항상 집에 있고 싶다고 한다. 대학생 중 100명을 표본추출하여 이에 대해 물어봤을 때, 16 ~ 19명 사이로 집에 있고 싶어하는 학생이 있을 확률을 구해보자.

1) 이항분포를 통해 대략적인 식만 나열해보기 $nCr\,p^x(1-p)^{(n-x)}$
$∑_{i=16}^{19}100Ci(0.2)^{i}(0.8)^{100-i}$

2) 연속성 수정을 고려해 정규분포에서의 범위 구해보기
집에 있고 싶어하는 학생의 확률 = 0.2 (p)
평균=np= $100(0.2)=20$
표준편차 $\sqrt{npq}=\sqrt((100)(0.2)(0.8))=4$

1) x=16일 때 표준점수
연속성 수정 = x- $\frac12$ = $\frac{31}2$
$z=\frac{X - \bar{x}}{\sigma}$ =- $\frac98$
2) x=19일때 표준점수
$z=-\frac18$
따라서 정규분포에서의 범위 $[-\frac98, -\frac18]=[-1.125, -0.125]$