📚 F분포란?
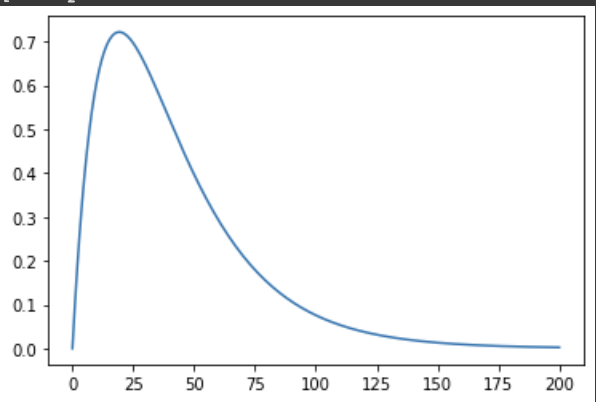
F분포의 확률변수는 두 개의 독립인 카이제곱분포 확률변수의 비로 정의한다.
! 카이제곱분포가 한 집단의 분산을 다룬다면, F분포는 두 집단의 분산을 다룬다.
이 과정에는 나눗셈이 쓰인다.

확률밀도함수는 다음과 같이 흉악하게 생겼다.
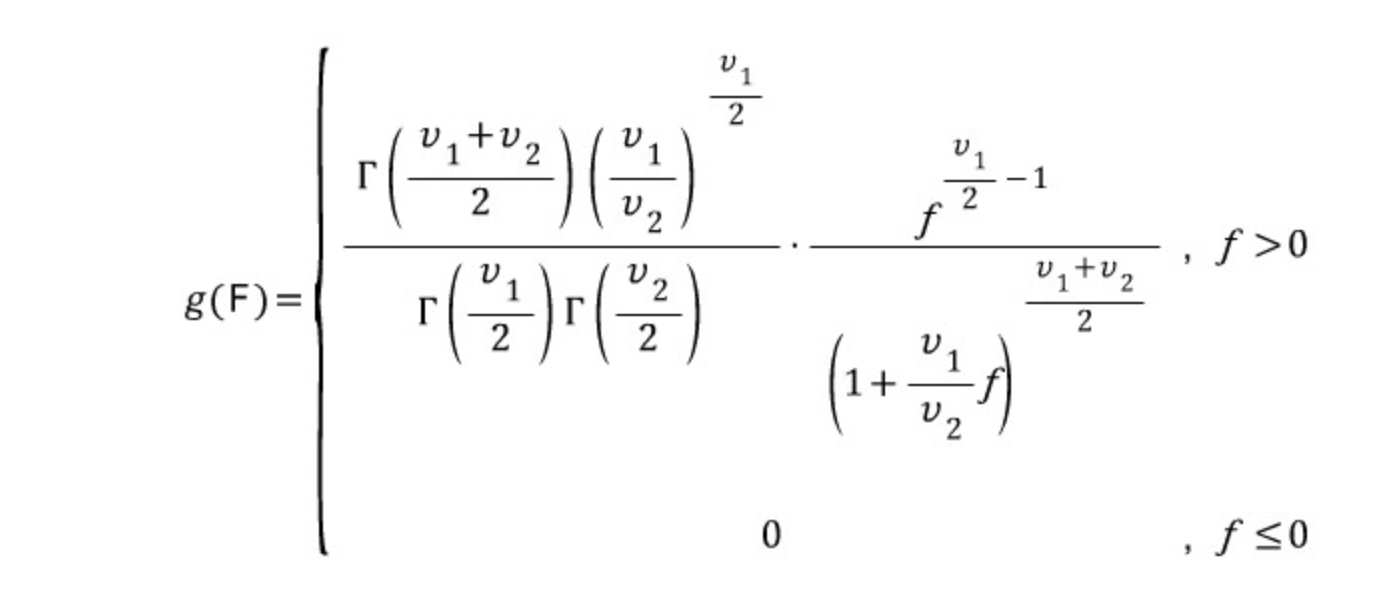
다만 여느 복잡한 확률변수처럼, 우리가 이를 직접적으로 계산할 일은 없다시피 하다. 이미 뛰어나신 수학자님들이 값을 계산해서 F분포표를 만들어놨기 때문.
위에서 집단의 분산을 비교하기 위해서 나눗셈을 사용한다고 했는데,
이는 결과값에 따라 1이 나오지 않는다면 두 분산이 다르다는 결론을 도출할 수 있다.
💡 그래프의 오른쪽 면적을 적극적으로 활용하기 위해 대부분 분산이 작은 집단을 분모에, 분산이 큰 값을 분자에 놓는다고 한다
💡 아래 분포표를 봐도 알 수 있듯이 그래프에서 1보다 작은 왼쪽 면적은 거의 사용하지 않는다
💡 값이 1에 가까울수록 두 분산은 비슷하고, 멀어질수록 두 분산은 다르다.
그리고 카이제곱분포의 비로 정의하기에 양의 확률변수에 대해서만 정의된다.
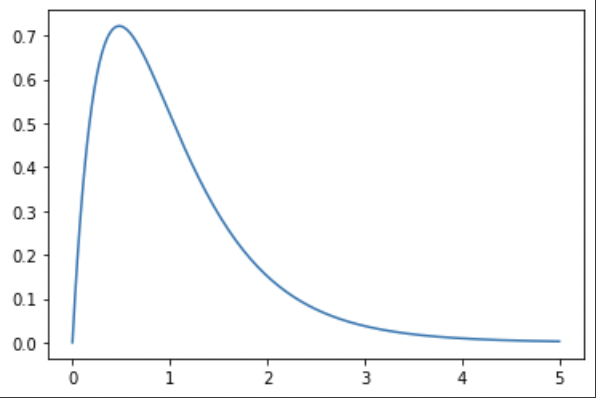
그림을 보면, 값이 1에 가까울수록 (두 집단의 분산이 비슷하다는 뜻) 분포가 많고, 멀어질수록 분포가 감소하는 것을 볼 수 있다. 이는 보통 비교를 할 때 💡비슷한 집단을 많이 비교를 하기 때문에 두 분산의 차이는 크지 않을 확률이 높기 때문이라고.
📚 활용
t분포와 카이제곱분포처럼 확률을 구할 때보다는 검정과정에서 많이 사용한다고 한다.
특히 ANOVA와 같은 분산분석을 할 때 F분포를 사용한다. 이 때 그래프의 축 값인 F값을 활용하는데, 그 표는 다음과 같다.
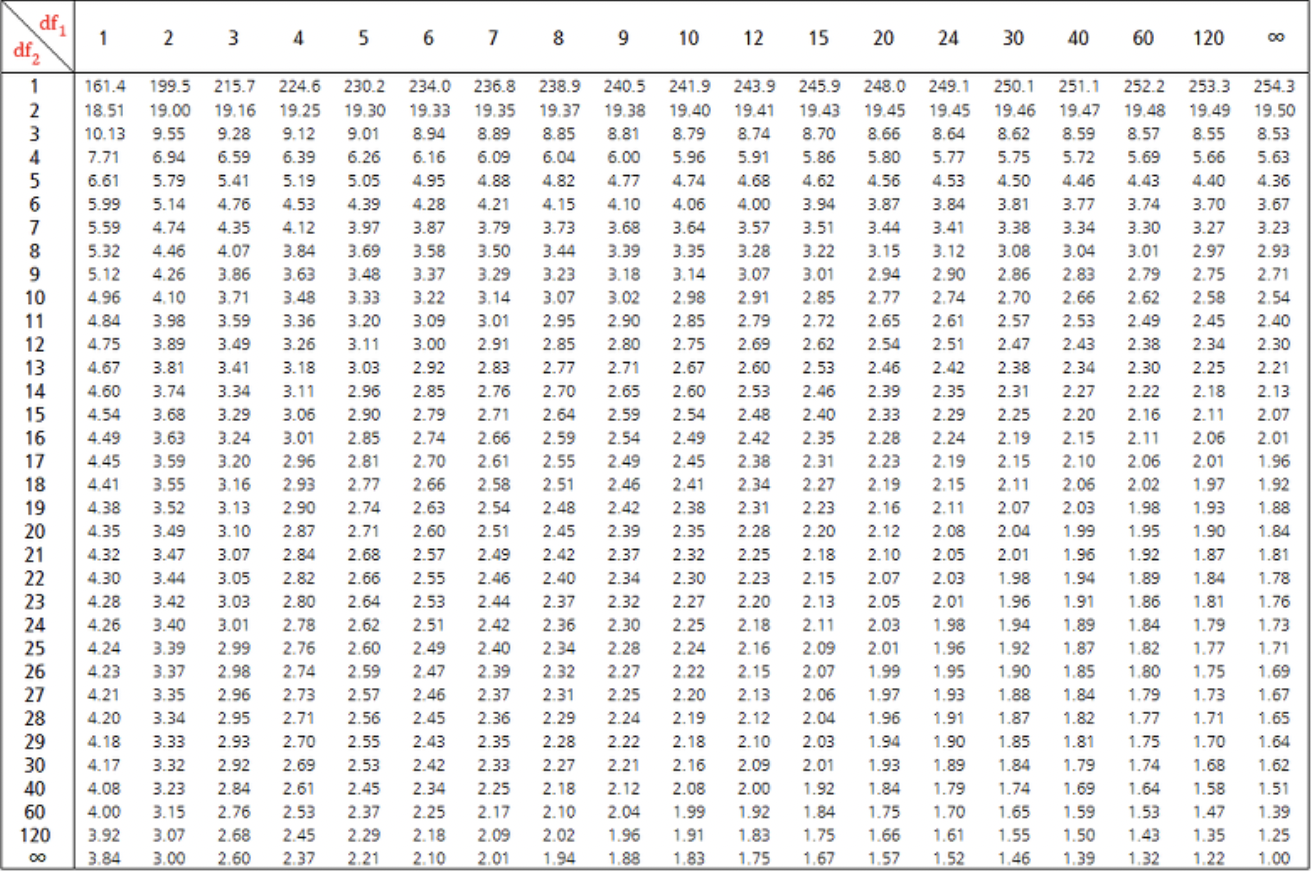
얘는 자유도가 2개라서 표가 많은데, 일단 0.05 유의확률의 표를 가져와봤다.
자유도가 두 개라서 도 두개가 되는데, 분모의 자유도가 2, 분자의 자유도가 1이다.
📚 그리기
scipy의 stats 모듈의 f().pdf() 함수를 통해서 쉽게 그릴 수 있다.
import scipy as sp
import numpy as np
x = np.linspace(0, 5, 201)
r1 = sp.stats.f(4, 50).pdf(x) # f의 인자 자유도(d1,d2)
plt.plot(x, r1)📚 요약
F분포는 두 집단의 분산을 비교하기 위해 사용하는 분포로, 주로 검정에 이용된다.
1에 가까울수록 두 집단의 분산이 비슷하다는 뜻이며, 1에서 멀수록 두 집단의 분산이 다르다는 뜻이다.
