📚 재표본추출
- 표본을 반복적으로 추출하여, 무작위 변동성을 알아보는 것.
- 머신러닝 모델의 정확성을 평가하고 향상시키기 위해 적용 가능.
- 부트스트랩 데이터 집합을 기반으로 각 표본 당 의사결정트리 예측의 평균을 구함으로써 평균 예측값을 구할 수 있다(배깅) - 데이터의 형식이 숫자형이던 이진형이던, 데이터의 크기가 같던 다르던, 데이터가 정규분포를 따르던 안 따르던 사용 가능하다.
📚 부트스트랩
어떤 분포에서 생성된 지 모르는 n개의 데이터가 있다고 하자. 부트스트랩을 이용하지 않으면 우리는 1개의 sample median만을 알 수 있다.
하지만 Bootstrap sampling을 r번 수행하면 총 r개의 sample이 주어지게 되고, 이를 통해서 조금 더 정확한 sample median을 구할 수 있다.
이렇게 r개의 표본을 만들어내면 그로부터 분포를 그릴 수 있고, 결과적으로 표본에 따라 평균이 얼만큼 변하는지를 (표본의 변동성) 알 수 있다.
정리하자면 모수의 분포를 모를 때 신뢰 구간을 가늠하는 방법 이라고 할 수 있겠다.
장점
- 심플하다. 개념이 단순히 많은 횟수의 비복원추출로 표본을 재생산해내는 것.
- 정규분포를 가정하는 것보다 신뢰성이 높다. (신뢰구간을 구할 수 있게 되므로)
- 표본의 통계량에 의존하지 않는다. 정규성이 전제될 필요가 없다.
단점
- 사용되는 추정치에 크게 의존하므로, 항상 점근적으로 유효한 결과를 도출하는 것은 아니다.
이는 이전에 포스팅한게 있으므로 링크를 건다.
[통계] 부트스트랩
📚 순열검정
- 순열 과정은 두 개 이상의 표본이 관여되며 통상적으로 A/B 혹은 기타 가설검정을 위해 사용되는 그룹이다.
순서는 다음과 같다.1) 첫 단계는 그룹 A와 그룹 B(그룹이 두 개라고 할 때)의 결과를 합친다.
-> 그룹 A와 그룹 B가 유의미한 차이가 없다는 귀무가설을 논리적으로 구체화한 것.
2) 결합된 데이터를 섞고 그룹 A와 동일한 크기의 표본을 무작위로 비복원추출한다. (이 때 다른 그룹의 데이터는 당연히 섞인다)
3) 나머지 데이터에서 그룹 B와 동일한 크기의 표본을 무작위로 비복원추출한다.
4) 원래 샘플에 대한 통계량과 무관하게, 추출한 표본에 대한 통계량을 기록한다.
5) 앞선 단계들을 반복하여 검정통계량의 순열분포를 얻는다.
이렇게 했을 때, 두 그룹이 통계적으로 차이가 없다면 원래 sample의 통계량이 순열분포 안쪽에 존재할 것이고, 차이가 있다면 순열분포 바깥쪽에 원래의 통계량이 존재하게 된다.
⭐️ 순열검정은 임의순열검정, 전체순열검정, 부트스트랩순열검정으로 나뉜다.
예제는 임의순열검정만 살펴볼 것인데, 전체순열검정과 부트스트랩순열검정의 특징은 다음과 같다.
👨🏫 전체순열검정
- 데이터를 무작위로 섞고 나누지 않고 실제로 나눌 수 있는 모든 조합을 찾는다.
- 샘플 크기가 비교적 작을 때만 효율적이다.
- 임의순열검정에서 셔플링을 많이 할수록 전체순열검정의 결과와 비슷해진다.
- 영모형이 어떤 유의수준 이상으로 더 '유의미하다'보다 정확한 결론을 제공하므로, 정확검정 이라고도 한다.
👨🏫 부트스트랩 순열검정
- 임의순열검정의 2,3단계 무작위 추출을 비복원으로 하지 않고 복원추출로 한다.
- 모집단에서 개체를 선택할 때, 개체를 처리군에 할당할 때 모두 임의성을 가지게 된다.
😎 임의순열검정 예제
데이터는 https://github.com/gedeck/practical-statistics-for-data-scientists/blob/master/data/web_page_data.csv 에서 가져왔다.
실습은 [데이터 과학을 위한 통계학] 을 참고했다.
🎮 데이터 읽어오기
import pandas as pd
session_time = pd.read_csv('/content/drive/MyDrive/KHUDA/통계학 스터디/2주차_통계적 실험과 유의성검정/data.csv')
session_time📦 box plot 그리기
import matplotlib.pyplot as plt
ax = session_time.boxplot(by='Page', column='Time')
ax.set_xlabel('')
ax.set_ylabel('Time (in seconds)')
plt.suptitle('')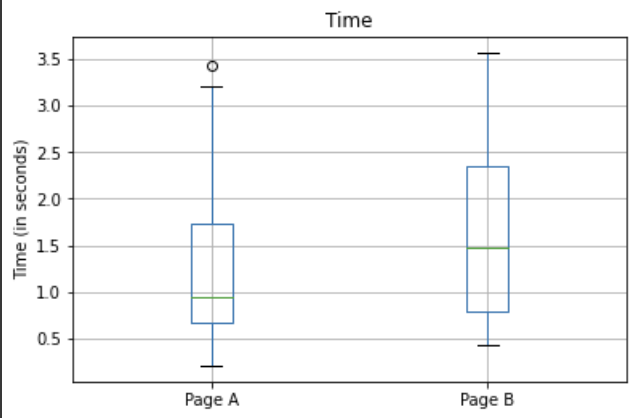
그래프로 봤을 때는 page B에서 사람들이 사이트에 더 오래 머무는 것 같다.
이게 유의미한 통계적 차이가 있을까?
🎲 순열검정 함수 생성
import random
def perm_fun(x, nA, nB):
n = nA + nB #데이터를 합친다
idx_B = set(random.sample(range(n), nB)) #B 크기의 무작위 그룹
idx_A = set(range(n)) - idx_B #A 크기의 무작위 그룹
return x.loc[idx_B].mean() - x.loc[idx_A].mean() #무작위 그룹의 평균 차이import numpy as np
nA = session_time[session_time['Page'] == 'Page A'].shape[0] #그룹 A의 크기
nB = session_time[session_time['Page'] == 'Page B'].shape[0] #그룹 B의 크기
perm_diffs = [perm_fun(session_time.Time, nA, nB) for _ in range(1000)] #1000번 무작위 순열 생성📊 히스토그램 그리기
mean_a = session_time[session_time['Page'] == 'Page A'].Time.mean()
mean_b = session_time[session_time['Page'] == 'Page B'].Time.mean()
fig, ax = plt.subplots(figsize=(5, 5))
ax.hist(perm_diffs, bins=11, rwidth=0.9)
ax.axvline(x = mean_b - mean_a, color='black', lw=2)
ax.text(50, 190, 'Observed\ndifference', bbox={'facecolor' : 'white'})
ax.set_xlabel("Session Time differences (per seconds)")
ax.set_ylabel("Frequency")
plt.tight_layout()
plt.show()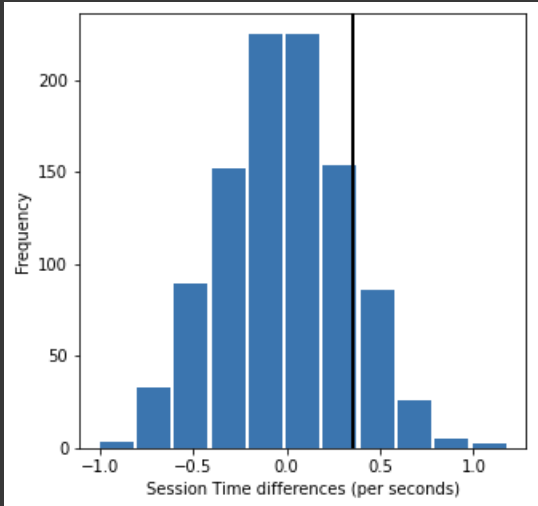
무작위 순열로 만든 데이터들로 분포를 그려봤을 때, 실제로 관찰된 차이가 순열분포 내에 존재하는 것을 알아냈다.
그렇다면 실제로 관찰된 차이보다 더 극단적으로 차이가 발생할 확률은 얼마일까?
# 무작위 순열로 구한 세션 시간 차이가 실제 관찰된 것보다 클 확률?
print(np.mean(perm_diffs > mean_b - mean_a))무작위 순열로 만든 분포이므로 값이 모두 다르겠지만, 필자는 0.135가 나왔다.
따라서 실제 관찰값보다 극단적인 케이스가 나올 확률은 13.5%.
관찰된 값이 순열분포 내에 있으므로 통계적으로 유의미한 차이가 있지는 않지만,
관찰된 값 혹은 그 이상의 차이가 13.5% 확률로 발생할 수 있다는 의미이다.
