📚 통계적 유의성

• 통계학자의 실험 결과가 우연히 일어난 것인지, 혹은 우연히 일어날 수 없는 극단적인 것인지를 판단하는 방법이다.
• 결과가 우연히 벌어질 수 있는 변동성의 바깥에 존재한다면 이것을 통계적으로 유의하다 라고 한다.

❌ 1종 오류

😵‍💫 귀무가설이 참이지만 귀무가설을 기각하는 경우

❌ 2종 오류

🧐 귀무가설이 거짓이지만 귀무가설을 채택하는 경우

가설검정의 목적은 '우연히 일어난 일을 유의미하다고 받아들이지 않는 것'이기에 보통 1종 오류를 최소화하도록 가설을 설계한다.

🔠 $\alpha$ (유의수준)

결과가 "통계적으로 유의미하다"로 간주되기 위해, 우연에 의한 결과가 능가해야 하는 비정상적인 가능성의 임계 확률.
1종 오류를 범할 확률.

말이 어렵다.. 하지만 직관적으로 생각해보자.
순열검정의 결과를 보면, 순열분포의 오른쪽으로 갈수록 '극단적인 값'이 우연히 발생할 확률은 작아졌다. 이는 집단 간 유의미한 통계적 차이가 있다는 소리이다.

근데 어느 선부터 우연이 아닌 것으로 치부할 것이냐?
이 '선'을 정한 것이 알파(유의수준)이 된다.

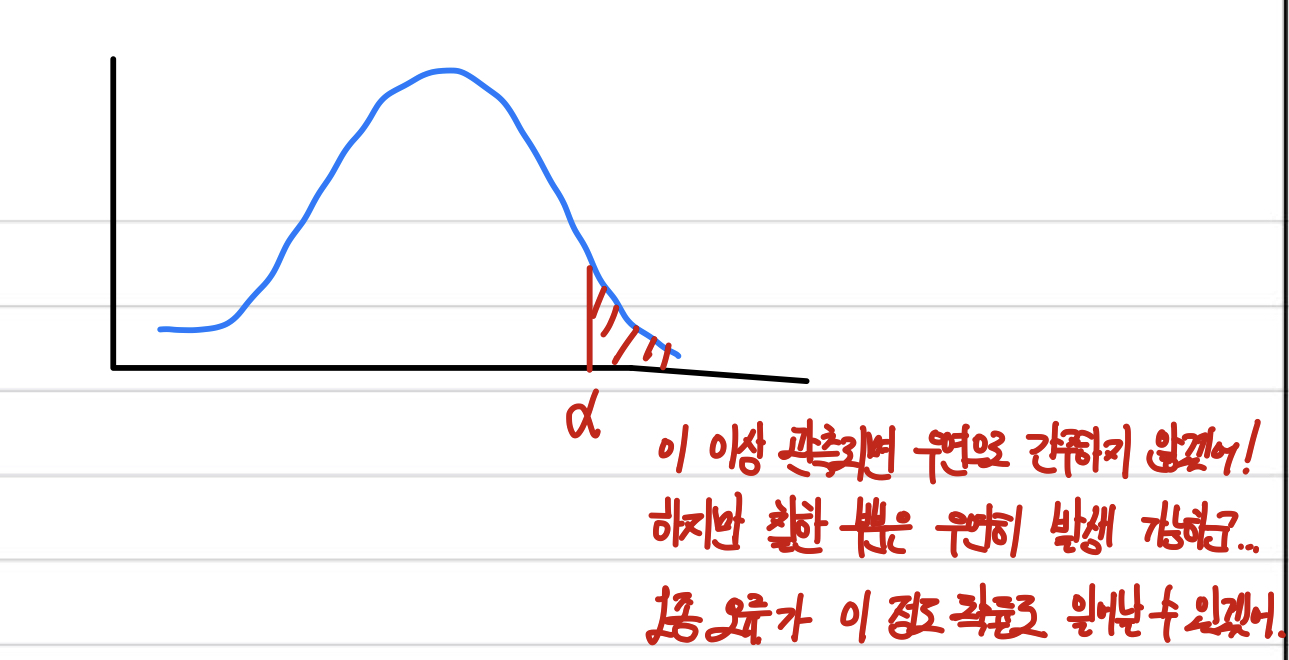
다만 설정한 부분은 우연히도 발생할 수 있는 부분이므로, 1종 오류(귀무가설이 참인데 기각)을 유발할 가능성이 있다. 그래서 유의수준이 "1종 오류를 범할 확률"이라는 그지같은 정의를 가지게 되는 것.
이렇게 생각하면 왜 p값이 설정한 알파값보다 작을 때 '통계적으로 유의미하다'라는 결론을 내릴 수 있는지 알 수 있다.

p값과 헷갈릴 수 있는데, p값은 실제로 검정을 통해 측정된 값이고, 알파는 실험자가 사전에 '이 정도를 넘으면 유의미한 것으로 간주하겠어' 라고 선언해놓는 것.

최근에는 말도 많고 탈도 많다는데, 관례적으로 5%(0.05) 혹은 1%를 많이 쓴다고 한다.

💉 p-value(유의확률)

귀무가설이 맞다고 가정할 때, 얻은 결과보다 극단적인 결과가 실제로 발생할 확률.
랜덤 모델이 주어졌을 때, 그 결과가 관찰된 결과보다 더 극단적일 확률.

💡 앞선 임의순열검정의 예제 에서 보았듯이, 데이터를 무작위 순열로 뽑아 분포를 만들고, 관측값이 우연에 의하여인지 혹은 유의미한 차이가 있는지 순열분포와 관측값의 비교를 통해서 알 수 있었다.
마지막에 관측값보다 극단적인 값이 등장할 확률을 출력해봤는데, 이를 p-value라고 한다.