📚 About 카이제곱분포

확률변수 가 카이제곱분포를 따르면 로 표현한다고 한다.
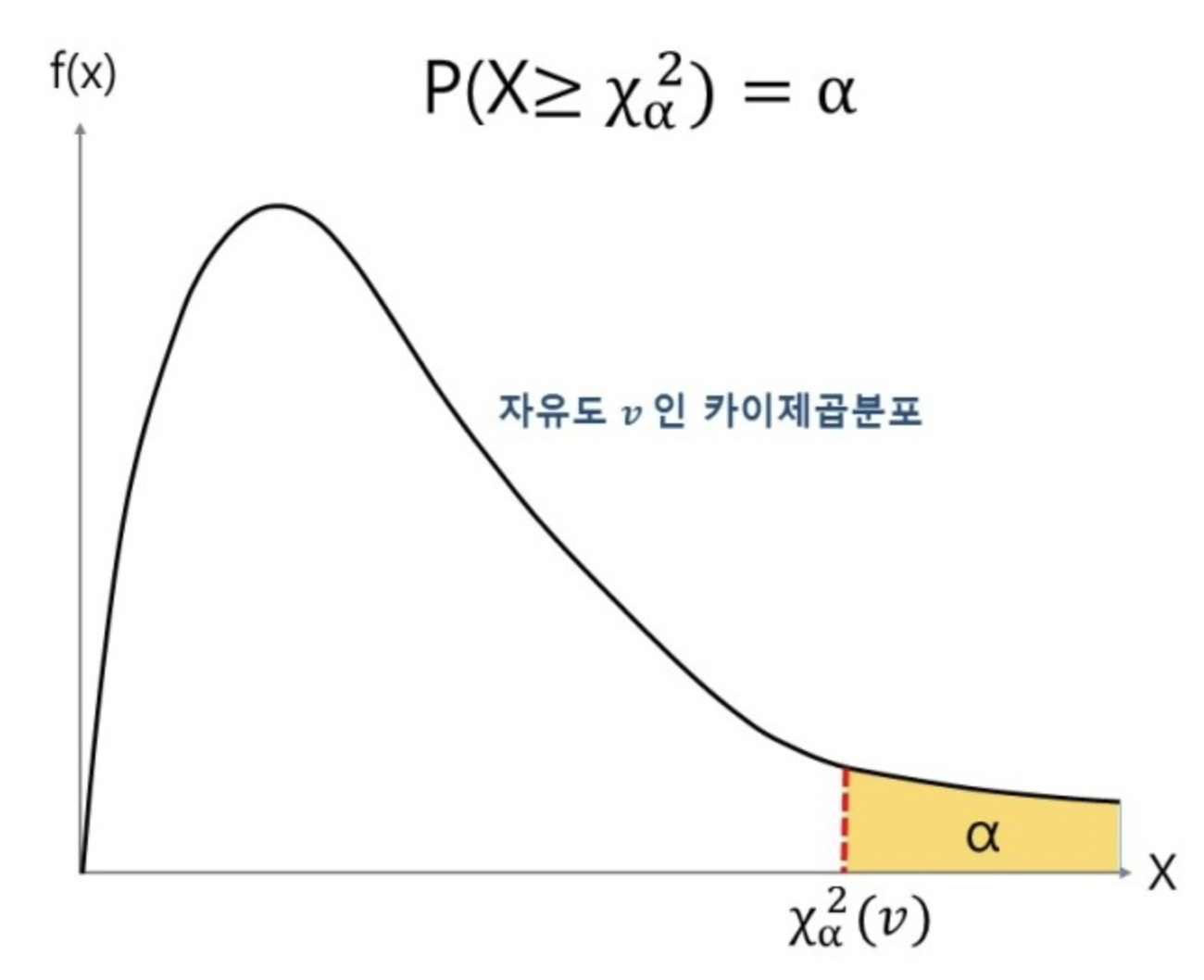
확률밀도함수를 그래프로 그려보면 다음과 같다. 그래프는 자유도 에 따라 달라진다.

확률변수 가 자유도 인 카이제곱분포를 따르면, 그 확률은 라고 한다.
📚 시뮬레이션
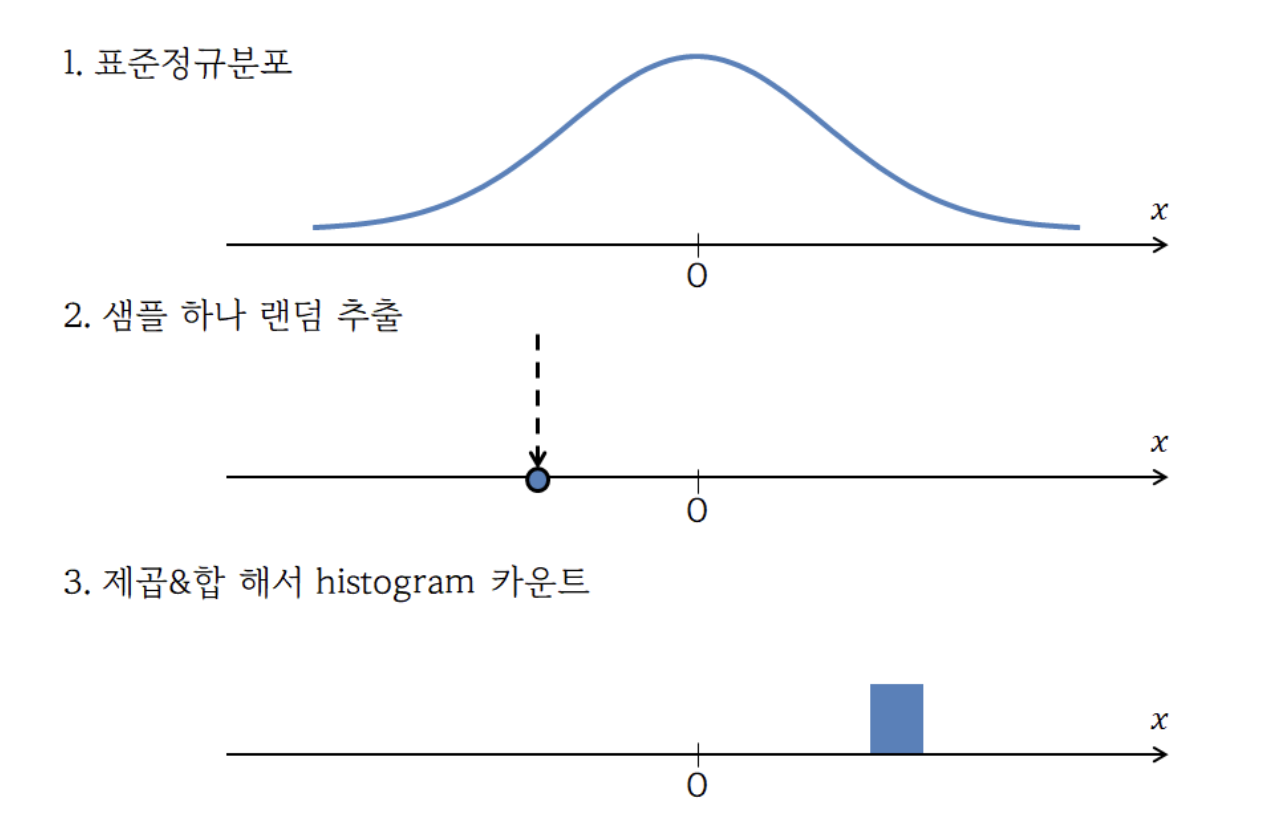
위 그림은 일 때 카이제곱분포가 형성되는 과정이다. (출처 : https://angeloyeo.github.io/2021/12/13/chi_square.html)
계속해서 샘플을 뽑고 제곱&합해서 카운트하면 아래와 같은 히스토그램이 나타난다고.
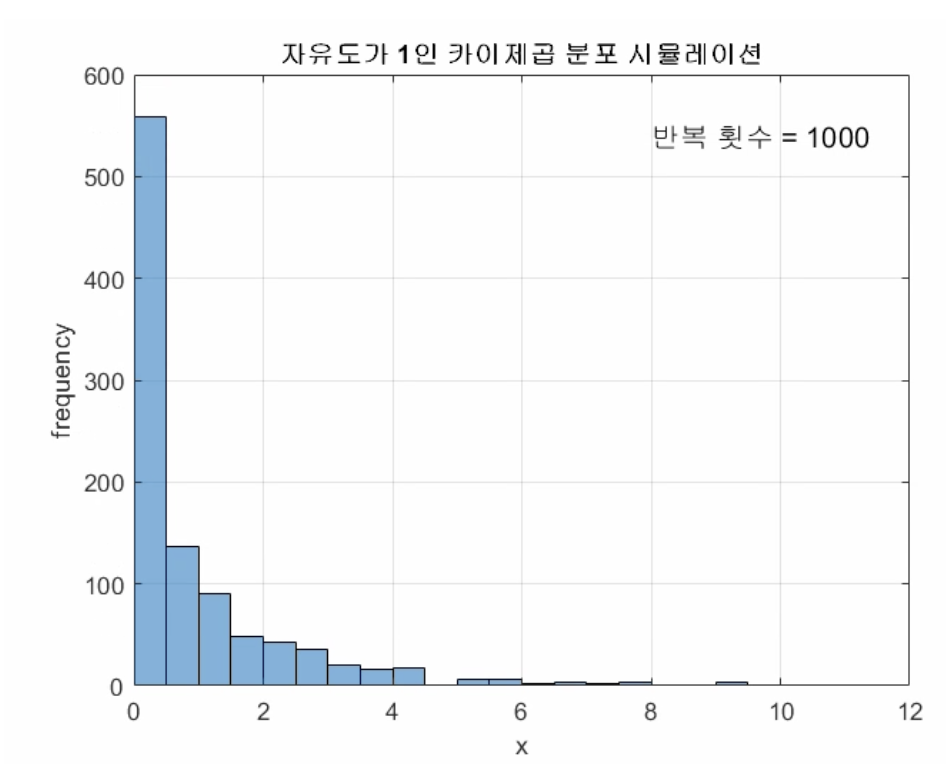
이는 자유도 1인 카이제곱분포와 비교해보면 상당히 일치하게 된다.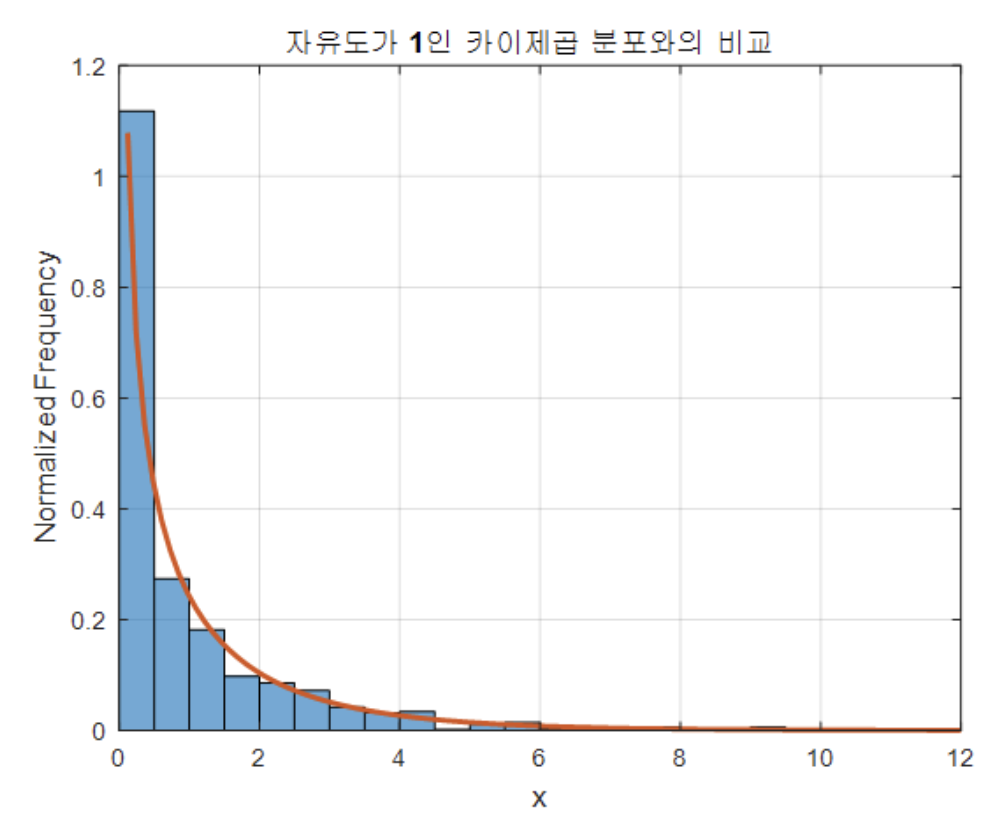
가 늘어나면 늘어날수록 뽑는 샘플의 수가 늘어난다. 각각 모두 제곱해서 더하면 된다 !
💡 모든 값을 제곱해서 더하기 때문에 양의 확률변수에서만 존재한다
📚 활용
카이제곱검정은 오차나 편차를 분석할 때 쓰인다고 한다.
중심극한정리에 따라, 표본오차의 분포는 정규분포에 가깝게 된다. (샘플 수가 많을수록)
따라서 그로부터 카이제곱분포를 그릴 수 있게 되고, 표본분산을 통해 모분산을 추측하는 것이 주된 용도라고 한다.
📚 카이제곱 검정
적합도 검정 (goodness-of-fit test)와 교차 분석(cross tabulation analysis)을 이용할 때 카이제곱 분포를 많이 이용한다고.

검정통계량 공식에서 는 관찰도수, 는 기대도수이므로 는 편차의 제곱이라는 것을 알 수 있따. 로 나눠준 것은 정규화를 하는 것이라고 볼 수 있고.
얘는 특정 정규분포를 따르고, 이것들의 합은 카이제곱 분포를 따를 수 있다는 것을 증명할 수 있다고 한다.
다만 항상 카이제곱 분포를 따르지는 않고, 중심극한정리를 이용해 증명하기 때문에 전체 데이터의 크기가 충분해야 한다.
📚 적합도 검정
독립변수가 범주형 변수(categorical variable)이고 하나일 때, 이론적으로 기대되는 빈도의 분포와 관찰한 빈도의 분포를 비교하기 위해 사용한다고 한다.
예를 들어 사탕 봉지가 있다고 하자. 각 봉지에 5가지 맛의 사탕이 들어 있다고 가정한다.
그 중 1000개의 사탕을 뽑았다.
(예시는 https://www.jmp.com/ko_kr/statistics-knowledge-portal/chi-square-test/chi-square-goodness-of-fit-test.html 에서 가져와 각색했다.)
영가설은 "봉지마다 담긴 다섯 가지 맛의 비율이 동일할 것이다"이다.
따라서 사탕 봉지 안에 있는 사탕의 맛의 비율은 모두 같으니, 기댓값은 각 맛마다 200개는 있을 것이라 설정할 수 있다.
사탕의 맛은 범주형 변수이니 카이제곱분포를 통한 적합도 검정을 활용해볼 수 있다.

10봉지 합쳐서 사탕의 총 개수는 위 그림과 같다. 딱 봐도 200개와는 차이가 있지만, 이 오차가 '용납 가능한 수준인지' 혹은 '유의미한 맛별 비율의 차이가 있는 것인지' 검정하는 것.
📚 검정통계량 구하기
그래서 위에서 카이제곱 검정통계량 공식을 통해 통계량을 구해보면,
사과맛 : 180개이므로 , 이를 기대도수 200으로 나눠주면 2가 되고
라임맛 : 250개로 12.5,
체리 : 120개로 32,
오렌지와 포도는 동일하게 225개씩 있으므로 3.125가 된다.
이들을 모두 더해 검정 통계량은 52.75가 된다.
📚 가설 채택/기각
이제 이 통계량을 통해 우리의 영가설을 채택해야 할지 기각해야 할지 정할 수 있다.
보통 유의확률은 .05로 설정하므로 해당 값을 카이제곱 분포에서 찾아보자. 이 경우 자유도가 필요한데, 자유도는 표준분산을 구할 때처럼 이 된다.
간략하게 말하면, 총 개의 데이터가 있고 그들의 평균은 정해져있다고 하자. (모평균) 그러면 개까지의 데이터는 독립적이지만, 마지막 번째 데이터는 나머지 데이터에 종속되게 된다.
따라서 맛 변수는 총 5개이므로 자유도는 4. 자유도 4, 유의확률 .05인 카이제곱 값은 9.49이다.

출처 : https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=ktec21&logNo=221417326644
검정통계량과 비교했을 때, 유의확률 9.49 < 52.75이므로 영가설을 채택한다. 결론적으로 사탕의 5가지 맛 중 하나라도 다른 비율로 섞여있다고 보기 어렵고, 우연히 사탕을 골고루 뽑지 못했다고 보는 것이 합당하다.
📚 교차 검정
교차 분석은 범주형 변수가 여러 개인 경우에 적용하는 분석 방법이다. 목적은 범주 간 차이가 🚨기댓값에서 유의하게 벗어나는지🚨 확인하는 것.
Q. 교차 검정에서의 카이제곱분포량 구하기
색상에 대한 남녀의 색상 선호도를 조사한 분할표는 다음과 같다.
1) 파랑색을 선호하는 여학생의 기대도수를 구하고
2) 분할표의 검정통계량을 구해보자
3) 자유도는 몇일까?
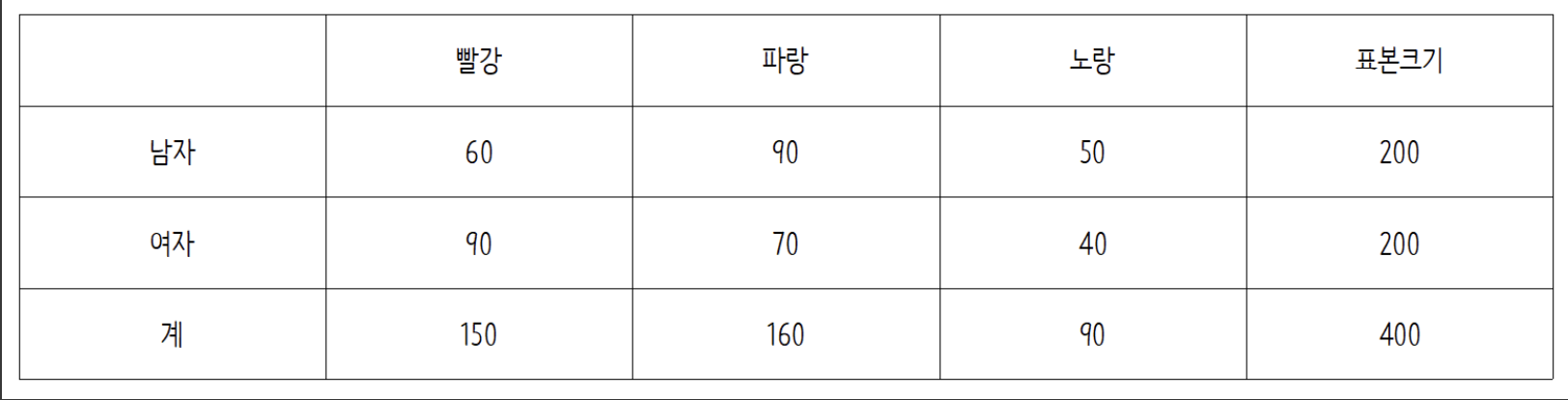
💡 A1. 파랑색을 선호하는 여학생의 기대도수는 해당 셀의 전체 열 * 전체 행 / 데이터의 갯수이므로 이 된다.
💡 A2. 우선 모든 셀의 기대도수를 구하면,
남자-빨강 = ,
여자-빨강 = ,
남자-파랑 = ,
여자-파랑 = ,
남자-노랑 = ,
여자-노랑 =
통계량을 계산하면
💡 A3. 자유도는 3행 2열이므로 (3-1)(2-1)=2이다.
추가로 이를 토대로 가설검정을 해보면, 카이제곱분포표에 의해 자유도 2, 유의확률 .05값은 5.99이므로,
통계량 9.62 > 유의확률 5.99이라서 영가설을 채택한다.
결과적으로 남녀간 색상 선호도는 통계적으로 유의미한 차이가 없다고 결론지을 수 있다.
📚 요약
카이제곱검정은 오차나 편차를 주로 다룬다. 때문에 기댓값과의 차이가 유의미한지 살피는 적합성 검정이나, 집단 간의 차이를 살피는 교차검정에 사용된다.
참고
https://angeloyeo.github.io/2021/12/13/chi_square.html
https://www.jmp.com/ko_kr/statistics-knowledge-portal/chi-square-test/chi-square-goodness-of-fit-test.html
