[FwFM] Field-weighted Factorization Machines

Intro

FFM 모델은 학습해야 하는 interaction term의 parameter 수가 $n$(#features) X $f$(#fields) X $k$(latent vector size)로 field가 많은 high-dimensional dataset에서는 비효율적이다. FwFM은 field interaction마다 weight를 주는 방법으로 이를 보완하고 효율적인 모델을 구현한다.

Data

• Field $F(i)$, $i=1, 2, ..., n$
• Feature $f_i$, $i=1, 2,... , m$
• Dataset $S = \{\bold{x}^{(s)}, y^{(s)}\}$, $\; y^{(s)} \in \{-1, 1\}$, $\; \bold{x}^{(s)} \in \{0, 1\}^m$

Model

FFM은 아래 식과 같이 interation term의 latent vector $\mathbf{v}$를 field별로 생성하기 때문에 parameter의 수가 많아진다.

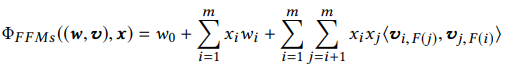
FwFM은 field별로 latent vector를 생성하지 않고 field interaction마다 weight $r_{F(i),F(j)}$를 주는 방법으로, FFM과 같이 field의 개념을 포함하면서도 parameter의 수를 줄여 효율적으로 모델을 학습할 수 있다.

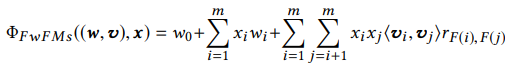
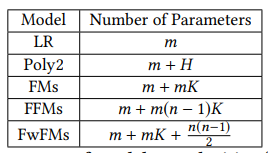
FwFM의 parameter 수는 FM에 field의 조합 $\frac{n(n-1)}{2}$를 더한 값으로 FFM에 비해 확연히 줄어든 것을 확인할 수 있다.

Note

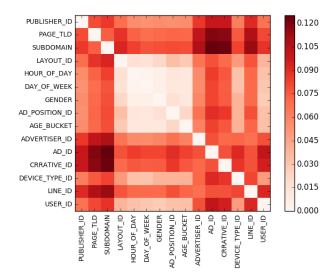
1. field와 target을 이용하여 MI(Mutual Information)을 계산한 그림은 아래와 같다. 이를 통해 각 field별로 interaction strength에 차이가 있는 것을 확인할 수 있다.
   $\rightarrow$ 데이터의 크기가 적당하다면 EDA 과정에서 아래와 같이 MI를 찍어보는 것도 좋을 것 같다.

2. FwFM은 interaction term과 동시에 linear term 또한 세 가지 방법으로 연구하였다.

   • FwFMs_LW: 가장 기본적인 linear 형태 ($\sum x_iw_i$)
   • FwFMs_FeLV: embedding vector $v_i$ 각각에 weight를 준 형태 ($\sum x_i <v_i, w_i>$)
   • FwFMs_FiLV: embedding vector $v_i$에 field별 weight를 준 형태 ($\sum x_i <v_i, w_f(i)>$)

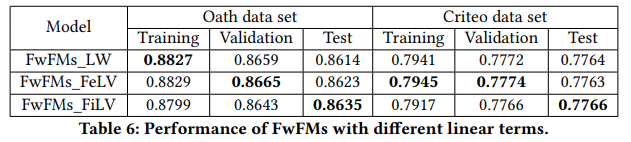
• Table 6.를 통해 LW와 FeLV, 두 방법이 Training과 Validation에서 AUC가 높은 것을 확인할 수 있는데, 이는 FiLV에 비해 두 방법이 parameter의 수가 많기 때문이다. 반면 Test에서는 FiLV의 성능이 높게 나오는데 이를 통해 FiLV가 더 나은 일반화 성능(generalization performance)을 보이는 것을 알 수 있다.

3. 기타 메모
   • criteo 데이터의 경우 imbalace가 심해서 downsampling 진행
   • $\tau$번 이하 등장한 feature들은 <NULL>로 대체
   • parameter의 수로 인한 성능 차이를 배제하기 위해 parameter의 수를 맞춘 상태로 모델 비교
   • embed_dim이 데이터의 크기보다 상당히 작았음에도 성능이 좋았음 (field-aware이라 그런 것으로 추정)

---

Code

※ CTR 시리즈의 모든 코드는 FuxiCTR을 참고했으며 함수 구조와 이름 등은 개인적으로 수정하여 사용하였다.

0. feature_dict은 각 feature의 설명을 dictionary 형태로 담고 있는 dictionary이고, EmbeddingDict()은 각 field의 embedding vector를 반환하는 ModuleDict()이다. ([batch_size, num_fields, embed_dim]의 stack 형태로 반환한다.)

1. FwFM 과정

   • EmbeddingDict으로 embedding 값을 생성한 후
   • InnerProduct를 통해 각 field별 조합을 생성하고
   • nn.Linear를 통해 weight $r_{F(i),F(j)}$를 곱한 결과를 리턴한다.

class FwFM(BaseModel):
    def __init__(self, feature_dict, linear_type='FiLV', embed_dim=CFG.embed_dim):
        super(FwFM, self).__init__()
        self._linear_type = linear_type
        self._num_fields = len(feature_dict)
        self._num_interactions = int(self._num_fields * (self._num_fields-1) / 2)
        self.embedding = EmbeddingDict(feature_dict=feature_dict)
        self.inner_product = InnerProduct(model='FwFM', feature_dict=feature_dict)
        self.inner_product_weight = nn.Linear(self._num_interactions, 1)

        if linear_type == 'LW':
            self.linear_weight = EmbeddingDict(embed_dim=1)
        elif linear_type =='FeLV':
            self.linear_weight = EmbeddingDict(embed_dim=embed_dim)
        elif linear_type =='FiLV':
            self.linear_weight = nn.Linear(len(feature_dict) * embed_dim, 1, bias=False)
        else:
            raise NotImplementedError('Only ["LW", "FeLV", "FiLV"] are supported')
        
        # training method
        # self.compile(CFG.optimizer, CFG.loss, CFG.learning_rate)
        # self.init_params()
        # self.model_to_device()

    def forward(self, inputs):
        X, y = self.inputs_to_device(inputs)
        X_emb = self.embedding(X)
        X_inner_product = self.inner_product(X_emb)
        inner_product_out = self.inner_product_weight(X_inner_product)

        if self._linear_type == 'LW':
            linear_out = self.linear_weight(X).sum(dim=1)
        elif self._linear_type == 'FeLV':
            linear_out = (X_emb * self.linear_weight(X)).sum(1, 2).view(-1, 1)
        elif self._linear_type == 'FiLV':
            linear_out = self.linear_weight(X_emb.flatten(start_dim=1))

        y_pred = linear_out + inner_product_out
        return {'y_true': y, 'y_pred': y_pred}

2. InnerProduct는 torch.triu와 torch.masked_select으로 torch.bmm을 통해 계산한 interaction matrix의 upper right triangle에 해당하는 interaction을 반환한다.

class InnerProduct(nn.Module):
    def __init__(self, feature_dict, model='FM', X_dim=None, device=CFG.device):
        super(InnerProduct, self).__init__()
        self._model = model
        self._num_fields = len(feature_dict)
        self._num_interactions = int(self._num_fields * (self._num_fields - 1) / 2)

        if model == 'FwFM':
            p, q = zip(*list(itertools.combinations(range(self._num_fields), 2)))
            self.field_p = nn.Parameter(torch.LongTensor(p), requires_grad=False)
            self.field_q = nn.Parameter(torch.LongTensor(q), requires_grad=False)
            self.upper_traingle_mask = torch.triu(
                torch.ones(self._num_fields, self._num_fields), 1
            ).type(torch.bool).to(device)

    def forward(self, X_emb):
        if self._model == 'FM':
            sum_of_square = X_emb.sum(dim=1) ** 2
            square_of_sum = torch.sum(X_emb ** 2, dim=1)
            fm_out = (sum_of_square - square_of_sum) * 0.5
            return fm_out.sum(dim=-1, keepdim=True)

        elif self._model == 'FwFM':
            batch_mat_mul = torch.bmm(X_emb, X_emb.transpose(1, 2))
            flat_triu = torch.masked_select(batch_mat_mul, self.upper_traingle_mask).view(-1, self._num_interactions)
            return flat_triu

---

Field-weighted Factorization Machines for Click-Through Rate Prediction in Display Advertising
FuxiCTR Github