선형 회귀
실제 값과 예측 값의 차이를 최소화 하는 직선형 회귀선을 최적화 하는 방식
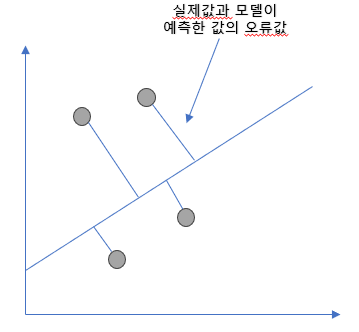
전체 데이터의 잔차(오류 값) 합이 최소가 되는 모델을 만드는 것
오류 값은 +나 -가 될 수 있음(예기치 않게 오류값이 줄어 들 수도 있음)
1. 절대값을 취해서 계산(MAE)
2. 오류 값의 제곱을 더해서 구하는 방식(RSS)
RSS를 비용함수로 지칭
종류
1. 일반 선형 회귀 : RSS를 최소화 할 수 있도록 회귀 계수를 최적화, 규제를 적용하지 않은 모델
2. 릿지(Ridge) : 선형 회귀에 L2 규제를 추가한 모델
L2 규제 : 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소 시키기 위해 계수값을 더 작게 만드는 모델
3. 라쏘(Lasso) : 선형 회귀에 L1 규제를 적용한 방식
L1 규제 : 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 예측시 해당 피처가 선택되지 않게 하는 것
4. 엘라스틱넷(ElasticNet) : L1, L2 규제 함께 결합, 주로 피처가 많은 데이터셋에 사용
L1규제로 피처의 개수를 줄이고 L2규제로 계수의 값 크기 조
5. 로지스틱 회귀(Logistic Regression) : 분류에 사용되는 선형 모델이긴 하나 텍스트 분류와 같은 분야에서 뛰어난 예측 성능을 보여줌
예제
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x_train, y_train)
pred = model.predict(x_test)
mean_squared_error(y_test, pred)
오차의 숫자는 작을 수록 좋은 것
