[프로그래머스 / Level 1] 실패율

김나쁜 Kimbad·2022년 8월 18일

코딩테스트

목록 보기

14/22

🚩 문제

문제설명

슈퍼 게임 개발자 오렐리는 큰 고민에 빠졌다. 그녀가 만든 프랜즈 오천성이 대성공을 거뒀지만, 요즘 신규 사용자의 수가 급감한 것이다. 원인은 신규 사용자와 기존 사용자 사이에 스테이지 차이가 너무 큰 것이 문제였다.

이 문제를 어떻게 할까 고민 한 그녀는 동적으로 게임 시간을 늘려서 난이도를 조절하기로 했다. 역시 슈퍼 개발자라 대부분의 로직은 쉽게 구현했지만, 실패율을 구하는 부분에서 위기에 빠지고 말았다. 오렐리를 위해 실패율을 구하는 코드를 완성하라.

실패율은 다음과 같이 정의한다.

스테이지에 도달했으나 아직 클리어하지 못한 플레이어의 수 / 스테이지에 도달한 플레이어 수

전체 스테이지의 개수 N, 게임을 이용하는 사용자가 현재 멈춰있는 스테이지의 번호가 담긴 배열 stages가 매개변수로 주어질 때, 실패율이 높은 스테이지부터 내림차순으로 스테이지의 번호가 담겨있는 배열을 return 하도록 solution 함수를 완성하라.

제한사항

스테이지의 개수 N은 1 이상 500 이하의 자연수이다.

stages의 길이는 1 이상 200,000 이하이다.

stages에는 1 이상 N + 1 이하의 자연수가 담겨있다.

각 자연수는 사용자가 현재 도전 중인 스테이지의 번호를 나타낸다.

단, N + 1 은 마지막 스테이지(N 번째 스테이지) 까지 클리어 한 사용자를 나타낸다.

만약 실패율이 같은 스테이지가 있다면 작은 번호의 스테이지가 먼저 오도록 하면 된다.

스테이지에 도달한 유저가 없는 경우 해당 스테이지의 실패율은 0 으로 정의한다.

입출력 예

N stages result
5 [2, 1, 2, 6, 2, 4, 3, 3] [3,4,2,1,5]
4 [4,4,4,4,4] [4,1,2,3]

출처: 프로그래머스 코딩 테스트 연습, https://school.programmers.co.kr/learn/challenges

N	stages	result
5	[2, 1, 2, 6, 2, 4, 3, 3]	[3,4,2,1,5]
4	[4,4,4,4,4]	[4,1,2,3]

🌌 생각

실패율을 구하기 위해 해당 스테이지의 총 도전자 수와 현재 도전중인 스테이지가 필요하다.
최종 스테이지까지 클리어한 경우 유저는 마지막 스테이지에서 빼준다.
실패율 순으로 정렬하고 실패율이 동일하면 낮은 스테이지가 앞으로 오도록 정렬.
- 해당 스테이지 번호와 실패율을 동시에 가지고 있는 객체가 필요함.

📝 코드 작성

import java.util.*;

class Solution {
    public int[] solution(int N, int[] stages) {
        int[] answer = new int[N];
        double[] challenge = new double[N+1]; // 해당 스테이지의 총 도전자 수
        double[] currentStage = new double[N+1]; // 도전중인 스테이지
        List<double[]> fail = new ArrayList<double[]>(); // 실패율
        
        // stages에서 총 유저수와 클리어하지 못한 유저 수 추출
        for (int i=0; i<=stages.length-1; i++) {
            // 스테이지 총 도전자 수
            for (int j=0; j<=stages[i]-1; j++) {
                challenge[j]++;
            }
            // 클리어하지 못한 도전자 수
            currentStage[stages[i]-1]++;
            if (stages[i] == N+1) { // 최종 스테이지까지 클리어한 사용자
                challenge[N-1]--; 
                // 최종 스테이지 클리어한 사용자는 빼준다
            }
        }
        
        // 스테이지별 실패율 추출
        for (int i=0; i<N; i++) {
            if(challenge[i] == 0) {
                fail.add(new double[]{i,0});
            } else {
                fail.add(new double[]{i,currentStage[i] / challenge[i]});
            }
        }
        
        fail.sort((a,b)->Double.compare(b[1],a[1]));
        
        for (int i=0; i<fail.size(); i++) {
            answer[i] = (int)fail.get(i)[0]+1;
        }
        
        return answer;
    }
}

처음에 한참동안 씨름한 코드
다 만들고 나서 케이스 3개만 통과를 못하길래 도대체 왜 이러나 싶어서
이틀을 고민했다.
아예 엎고 처음부터 다시 짜려고 슬슬 짜던 도중에 문득 떠오른 생각이 있어서 수정하니 문제가 해결됐는데, 깨닫고 나니 문제는 별거 아니었다.
처음 짤 때 내 생각은 최종 스테이지까지 클리어한 사용자는,
예를 들면 N=4, stages[n]이 = 5인 경우는 최종 스테이지까지 클리어한 유저니까
challenge[N-1]--;를 해줘야 한다고 생각했다.
실패율을 구할 때 divided by zero 에러가 나오지 않을까 생각해서 넣었던건데
최종 스테이지를 통과했어도 스테이지에 도달한 플레이어 수가 필요한 거라 빼줄 필요는 없었다.
저 부분만 약간 수정하고 나니 정상적으로 돌아갔다.

import java.util.*;

class Solution {
    public int[] solution(int N, int[] stages) {
        int[] answer = new int[N];
        double[] currentStage = new double[N+1];
        double[] totalUser = new double[N+1];
        List<double[]> fail = new ArrayList<double[]>();
        
        for (int i=0; i<stages.length; i++) {
            currentStage[stages[i]-1]++; // 스테이지에 도달했으나 아직 클리어하지 못한 플레이어의 수
            for (int j=0; j<stages[i]; j++) {
                totalUser[j]++; // 스테이지에 도달한 플레이어 수
            }
        }
        
        // 스테이지별 실패율 추출
        for (int i=0; i<N; i++) {
            if(totalUser[i] == 0) {
                fail.add(new double[]{i,0});
            } else {
                fail.add(new double[]{i,currentStage[i] / totalUser[i]});
            }
        }
        
        fail.sort((a,b)->Double.compare(b[1],a[1]));
        
        for (int i=0; i<fail.size(); i++) {
            answer[i] = (int)fail.get(i)[0]+1;
        }
        
        return answer;
    }
}

✔️ 다른 사람의 코드

class Solution {
    public int[] solution(int N, int[] stages) {
        int[] answer = new int[N];
        double[] tempArr = new double[N];
        int arrLength = stages.length;
        int idx = arrLength;
        double tempD = 0;
        int tempI = 0;
        for (int i = 0; i < arrLength; i++) {
            int stage = stages[i];
            if (stage != N + 1)
                answer[stage - 1] += 1;
        }
        for (int i = 0; i < N; i++) {
            int personNum = answer[i];
            tempArr[i] = (double) personNum / idx;
            idx -= personNum;
            answer[i] = i + 1;
        }

        for (int i = 0; i < N; i++) {
            for (int j = 1; j < N - i; j++) {
                if (tempArr[j - 1] < tempArr[j]) {
                    tempD = tempArr[j - 1];
                    tempArr[j - 1] = tempArr[j];
                    tempArr[j] = tempD;

                    tempI = answer[j - 1];
                    answer[j - 1] = answer[j];
                    answer[j] = tempI;
                }
            }
        }
        return answer;
    }
}

수많은 정답 중 import 없이, sort() method 없이 푼 문제가 있어서 인상 깊었다.
실패율이 같을 경우의 정렬이 문제인건데, 마지막의 2중 for문으로 정렬을 시켜준다.
나는 정렬 방법이 생각나지 않아서 인터넷의 도움을 받았지만
이 경우는 정렬이 크게 어려운 문제는 아니었던 것 같아서 나도 구현을 시도해봤으면 어땠을까?
하는 생각이 들었다. 정렬 알고리즘은 수십가지가 있으니, 그 중에 간단한 건 만들 수 있게 하는게 좋겠다.
간단한 공부용 알고리즘 몇 가지를 나무위키에서 찾아 등록해 놓았다.

📚 정렬 알고리즘

출처 : 나무위키 정렬 알고리즘 문서

거품 정렬(Bubble sort)

버블 정렬의 시각화

1번째와 2번째 원소를 비교하여 정렬하고, 2번째와 3번째, ..., n-1번째와 n번째를 정렬한 뒤 다시 처음으로 돌아가 이번에는 n-2번째와 n-1번째까지, ...해서 최대 $\frac{n(n-1)}{2}$ 번 정렬한다.
한 번 돌 때마다 마지막 하나가 정렬되므로 원소들이 거품이 올라오는 것처럼 보여 거품정렬이다.

거의 모든 상황에서 최악의 성능을 보여준다. 단, 이미 정렬된 자료에서는 1번만 돌면 되기 때문에 최선의 성능을 보여준다. 이미 정렬된 자료를 정렬하는 바보짓을 왜 하냐는 의문이 들 수 있지만, 정렬 알고리즘은 자료가 정렬되어 있는지 아닌지는 모르고 작동하기 때문에 의미가 있다.
가장 손쉽게 구현하여 사용할 수 있지만, 만들기가 쉽고 직관적일 뿐이지 알고리즘적 관점에서 보면 대단히 비효율적인 정렬 방식이다. 다른 몇 가지 정렬 방식과 비교해도 효율이 대략 시망.

이해하기 쉽고 코드가 짧은 덕에 각종 교습서에서 정렬 알고리즘의 예시로 많이 보여주며, 입력량이 작으면 어지간한 비효율적인 방법도 씹어먹고 수행이 가능하지만 실제 개발에서는 전혀 쓰이지 않는다고 봐도 무방하다. 정말 어지간한 경우가 아닌 이상 버블 소트는 피해야 한다. 요즘은 웬만한 프로그래밍 언어 내부에 온갖 꼼수를 다 갈아넣은 고효율의 정렬 알고리즘이 내장되어 있어, 그냥 인클루드해서 갖다 쓰기만 하면 되는 세상이라 버블 정렬의 장점이 거의 없다. 내장 정렬이 더 편하니

선택 정렬(Selection sort)

선택 정렬의 시각화

버블 정렬이 비교하고 바로 바꿔 넣는 걸 반복한다면 이쪽은 일단 1번째부터 끝까지 훑어서 가장 작은 게 1번째, 2번째부터 끝까지 훑어서 가장 작은 게 2번째……해서 (n-1)번 반복한다. 어찌 보면 인간이 사용하는 정렬 방식을 가장 많이 닮았다. 어떻게 정렬이 되어 있든 일관성 있게 $\frac{n(n-1)}{2}$ 에 비례하는 시간이 걸린다는 게 특징. 또한, 버블 정렬보다 두 배 정도 빠르다

파생형으로 이중 선택 정렬(Double Selection Sort)도 있다. 이쪽은 끝까지 훑어서 최솟값과 최댓값을 동시에 찾아낸 뒤 최솟값은 1번째와 바꾸고 최댓값은 끝과 바꾼 다음 훑는 범위를 양쪽으로 한 칸씩 줄여서 반복하는 방식이다. 즉 선택 정렬에 칵테일 정렬 방식을 도입한 것. 이 방법을 쓰면 반복 횟수가 반으로 줄어든다.

삽입 정렬(Insertion sort)

삽입 정렬의 시각화

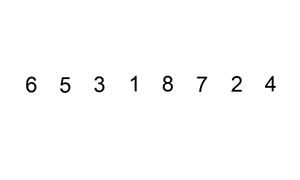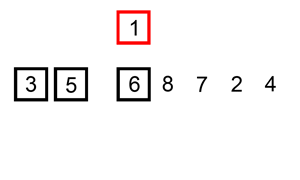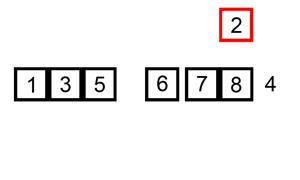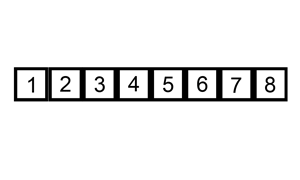
삽입 정렬을 알기 쉽게 만든 그림. 선택 정렬과 함께 인간에게 뭔가를 정렬하라고 하면 무의식적으로 사용하는 대표적인 알고리즘이다.
(예를 들어 카드 게임을 할 때나 번호대로 도서를 정리할 때. 필요한 임시 저장공간이 적고 컴퓨터와 달리 자료들을 밀어낼 때 소요시간이 없기 때문)

k번째 원소를 1부터 k-1까지와 비교해 적절한 위치에 끼워넣고 그 뒤의 자료를 한 칸씩 뒤로 밀어내는 방식으로, 평균적으론 $O$ ( $n²$ )중 빠른 편이나(최악의 경우가 $\frac{n(n-1)}{n}$ 에 비례한다.) 자료구조에 따라선 뒤로 밀어내는데 걸리는 시간이 크며, 앞의 예시처럼 작은 게 뒤쪽에 몰려있으면(내림차순의 경우 큰 게 뒤쪽에 몰려있으면) 그야말로 헬게이트다.
다만 이미 정렬되어 있는 자료구조에 자료를 하나씩 삽입/제거하는 경우에는 현실적으로 최고의 정렬 알고리즘이 되는데, 탐색을 제외한 오버헤드가 매우 적기 때문이다. 괜히 '삽입'이란 이름이 붙은 것이 아니다.

그밖에도 배열이 작을 경우에 역시 상당히 효율적이다.
일반적으로 빠르다고 알려진 알고리즘들도 배열이 작을 경우에는 대부분 삽입 정렬에 밀린다.
따라서 고성능 알고리즘들 중에서는 배열의 사이즈가 클때는 $O$ ( $n$ $log$ $n$ ) 알고리즘을 쓰다가 정렬해야 할 부분이 작을때 는 삽입 정렬로 전환하는 것들도 있다.