Ch 3-9. Rotations

rotation은 원래의 평면을 $θ$만큼 회전시키는 것을 origin은 고정된 점이다. 일반적으로 회전은 반시계 방향을 기준으로 한다.

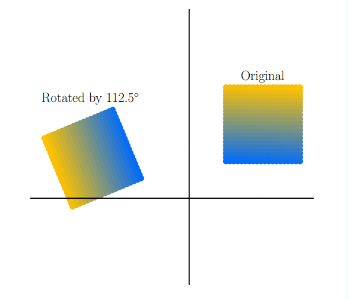
위 그림은 반시계방향으로 $112.5^∘$ 회전시키는 것으로 이때 transformation matrix는 다음과 같다.

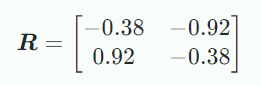
Rotations in $R^2$

$R^2$에서의 standard basis가 다음과 같을 때, 이 basis는 $R^2$에서의 표준 좌표계를 정의한다.

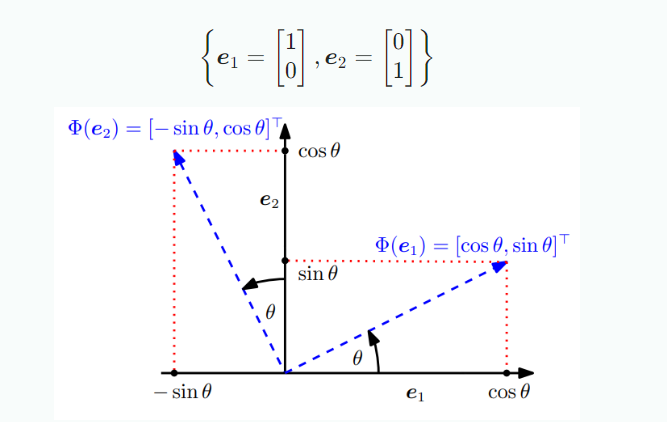
위 그림처럼 $θ$만큼 좌표계를 회전시킬 때 회전된 벡터는 여전히 선형 독립적이기 때문에 여전히 $R^2$의 기저이다.

Rotation $Φ$ 는 linear mapping이므로 rotation matrix $R(θ)$로 표현할 수 있다. 위 그림의 rotation matrix $R(θ)$는 다음과 같다.

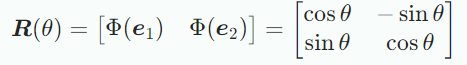
Rotations in $R^3$

$R^3$에서의 회전은 2차원 평면을 고정된 1차원 축에 대해서 회전시킨다. standard basis $e_1, e_2, e_3$가 회전된 $Re_1, Re_2, Re_3$는 서로 직교한다. 따라서 General rotation matrix $R$ 은 standard basis로부터 변환된 basis의 조합으로 얻을 수 있다. 2차원 이상의 차원에서 회전은 반시계방향이 어떤 방향인지 정의해야 하는데 이때, 아래 그림과 같이 한 basis vector를 중심 축으로 반시계 방향으로 회전시키면 된다.

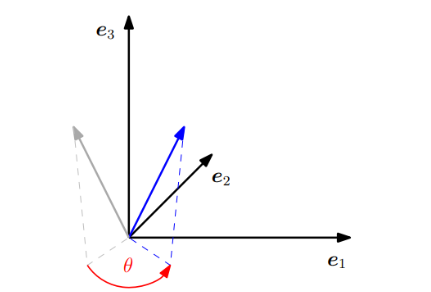
각각 3개의 기저벡터를 축으로 회전한 rotation matrix는 다음과 같다.

$e_1$에대한 회전은 $e_1$좌표는 고정되며 반시계 회전은 $e_2e_3$평면에서 수행된다.

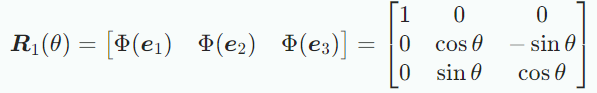
$e_2$와 $e_3$에대한 회전도 위와 같은 식으로 수행하면 된다.

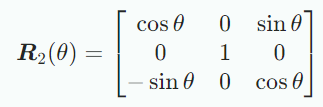
Rotations in $R^n$

n차원에서의 회전은 n-2차원을 고정하고 n차원 상에서 2차원 평면이 회전하는 것으로 제한할 수 있다. $V$를 n-차원의 Euclidean vector space라고 하고 $Φ:V→V$ 가 아래의 transformation matrix를 갖는다고 할 때, $R_{ij}(θ)$를 Givens Rotation이라 한다.

$R_{ij}(θ)$는 아래와 같은 element를 갖는 항등행렬 $I_n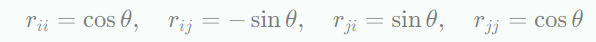$이다.

Properties of Rotations

Rotation은 orthogonal matrix로부터 유도되는 몇 가지 유용한 성질들이 있다.

1. rotation은 거리를 보존한다. 즉, $∥x−y∥=∥R_θ(x)−R_θ(y)∥$이다.
2. rotation은 각도를 보존한다. 따라서 Rθ(x)와 Rθ(y)간의 각도는 x와 y간의 각도와 같다.
3. 3차원 이상의 차원에서는 교환법칙이 성립되지 않으므로 회전이 적용되는 순서가 중요하다.