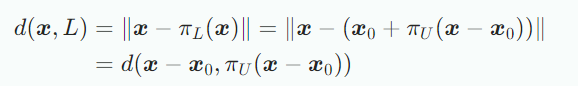Ch 3-8. Orthogonal Projections

Orthogonal Projections

머신러닝에서 주로 다루는 고차원의 데이터는 시각화하거나 분석하기 어렵기 어렵다. 고차원 데이터는 대부분의 차원이 불필요한 요소로 되어 있기 때문에 데이터의 압축손실을 최소화하기 위해 가장 정보를 많이 담고 있는 차원을 찾는 것이 이상적이다. 주어진 저차원 subspace에서 고차원 데이터의 orthogonal projection(정사영)은 가능한 많은 정보를 유지하고, 원본 데이터와의 차이나 오차를 최소화한다.

벡터공간 $V$, 부분공간 $U⊆V$가 있을 때, linear mapping $π$가 $π^2=π∘π=π$를 만족한다면 $π$를 projection이라고 한다.Linear mapping은 transformation matrix로 표현될 수 있기 때문에, linear mapping $π$ 는 projection matrices $P_π$로 표현될 수 있다. $π^2=π∘π=π$은 ${P^2}_π=P_π$를 만족한다.

Projection onto One-Dimensional Subspaces (Lines)

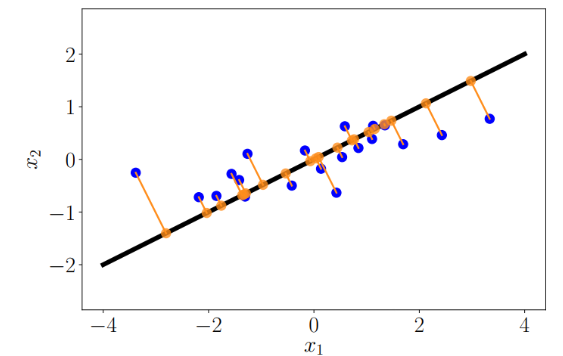
원본 데이터로부터 기저벡터가 $b∈R^n$인 1차원 subspace인 직선이 주어졌을 때 이 직선은 b에의해 span되는 subspace $U$이다.$x∈R^n$을 $U$로 투영할 때, $x$에 가장 가까운 벡터 $π_U(x)∈U$를 찾는다. $π_U(x)$의 속성은 다음과 같다.

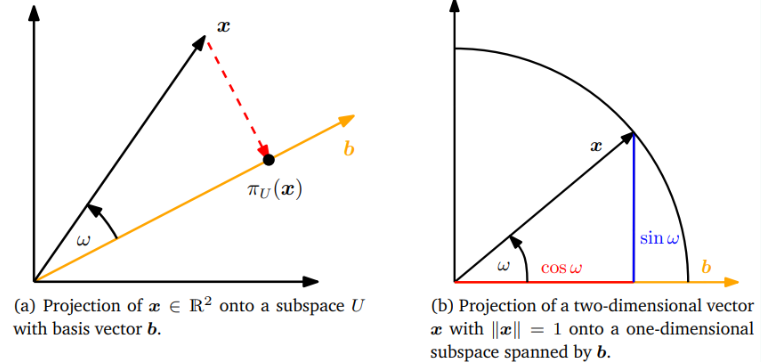
$π_U(x)$는 x와 가장 가깝다. 즉, 거리 $∥x−π_U(x)∥$가 최소다. 이는 $x−π_U(x)$가 $U$에 직교하며 이는 b와도 직교하며 $⟨π_U(x)−x,b⟩=0$가 만족한다는 뜻이다.
$π_U(x)$는 $U$의 element이므로 기저 b로 표현가능하므로 $π_U(x)=λb$이다.

다음의 3단계로 projection matrix $P_π$를 결정할 수 있다.

1. 다음의 orthogonality condition을 통해 coordinate $λ$ 를 찾을 수 있다.
   
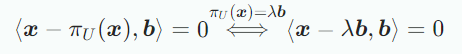
   내적의 bilinearity을 이용하여 다음 식을 도출할 수 있고,
   
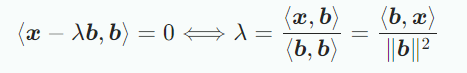
   내적은 symmertic하다는 사실을 이용하여 내적으로 dot product를 사용하면 다음 식이 도출된다.
   
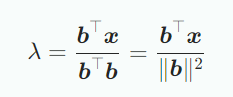
   $∥b∥=1$라면 projection의 coordinate $λ$는 $b^⊤x$로 주어진다.

2. 위의 식에서 $λ$를 얻었으므로 projection point $π_U(x)$를 구할 수 있다.
   
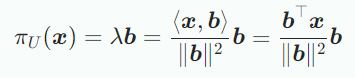
   $π_U(x)$의 길이는 다음과 계산할 수 있다.
   
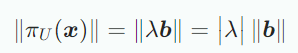
   projection의 길이는 $b$의 길이에 $λ$배 한 것과 같고 위 식 $λ$는 기저벡터 $b$에 대한 $π_U(x)$의 coordinate다. 내적으로 dot product를 사용하면 아래식을 얻을 수 있다.
   
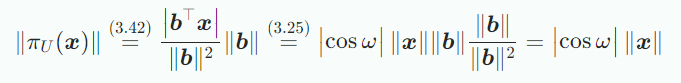
   $w$는 x와 b사이의 각도이다.

3. 마지막으로 projection matrix $P_π$를 찾는다. 내적을 dot product라 하면 다음 식을 통해
   
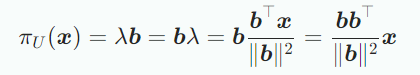
   projection matrix를 구할 수 있다.
   

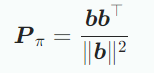
   Projection $π_U(x)$sms projection 된 후에도 n차원이며 스칼라값이 아니지만 더이상 n개의 좌표를 필요로 하지 않고 기저 b에 대해 $λ$ 하나로 표현가능하다.

Projection onto General Subspaces

1 이상 m차원 부분공간 $U$에 orthogonal projection하느 경우를 살펴보자. 아래 그림은 3차원 데이터를 2차원으로 projection하는 것을 보여준다.

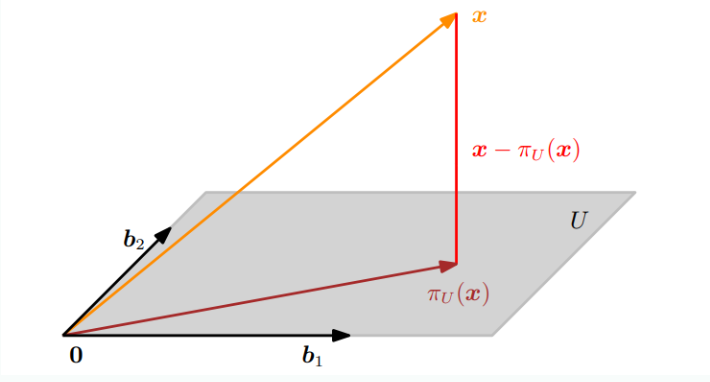
$U$의 기저를 $(b_1,..., b_m)$이라고 할 떄 모든 $U$로의 projection $π_U(x)$는 $U$의 element다 따라서 다음과 같은 기저들의 선형결합으로 표현할 수 있다.

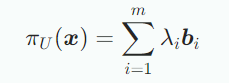
1차원으로 투영하는 방법과 같이 3단계를 통해 구할 수 있다.

1. projection의 coordinates $λ_1,…,λ_m$을 찾아야 한다.

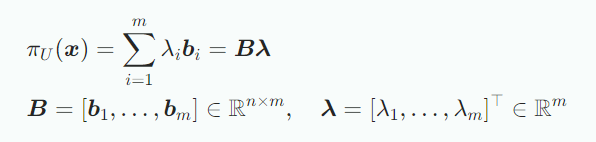
$x$에 가장 가깝다는 것은 $π_U(x)$와 $x$를 연결하는 모든 벡터가 $U$의 기저벡터와 직교한다는 것을 의미한다. 따라서 동시에 만족해야는 m개의 조건들이 있다. 여기서 내적은 dot product다.

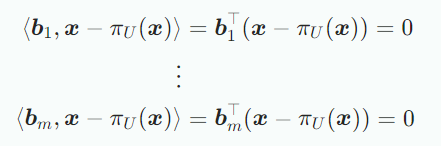
$π_U(x)=Bλ$이므로 위 식은 다음과 같아진다.

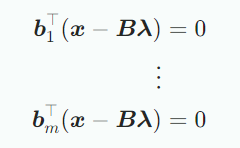
따라서 다음의 homogeneous linear equation system을 얻을 수 있다.

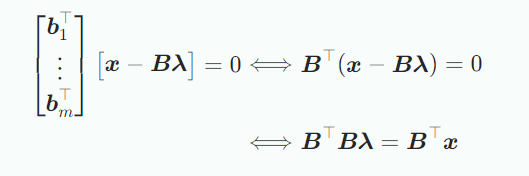
여기서 마지막 표현식을 normal equation이라 하고 $(b_1,..., b_m)$이 $U$의 기저이고 따라서 선형독립이기 때문에 $B^⊤B$는 regular이고 역행렬이 존재하므로 coordinate는 다음과 같다.

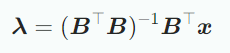
$(B^⊤B)^{-1}B^⊤$을 유사역행렬이라 하며 이를 사용하루수 있는 조건은 $(B^⊤B)$가 positive definite해야 하며 이는 $B$가 full rank임을 의미한다.

2. $π_U(x)=Bλ$이므로 위의 식으로 부터 다음을 구할 수 있다.

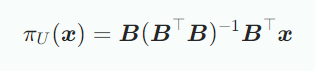
3. 위 식으로부터 $P_πx=π_U(x)$를 풀면 projection matrix를 구할 수 있다.

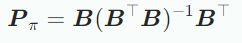
projection $π_U(x)$는 m차원 subspace $U$에 놓여있지만 $R^n$의 벡터이다. $U$의 기저벡터와 m개의 coordinate로 표현할 수 있을 뿐이다.

projection은 해가 없는 선형 방정식 Ax=b에서 사용할 수 있다. 해가 없다는 것은 b가 A의 span상에 놓여 있지 않다는 뜻으로 근사해를 통해 풀 수 있다. 근사해는 A에 의해 span되는 부분공간에서 b와 가장 가까이 있는 해를 찾는 것이다. 즉, A의 열들이 의해 span되는 부분공간에 대한 b의 정사영을 계산하는 것이다. 이러한 해를 least-squars solution of an overdetermined system이라 한다.

기저벡터가 $b_1,...., b_k$인 부분공간 $U$에 투영되는 $x$의 projection을 살펴보면 만약 이 기저벡터가 orthonormal basis라면, $B^⊤B=I$이므로 projection equation은 다음과 같다.

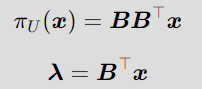
Gram-Schmidt Orthogonalization

Gram-Schmidt method는 벡터공간 V의 어떤한 기저도 orthogonal/orthonormal basis로 변환하도록 해주는 방법으로 이렇게 변환 된 기저는 항상 존재하며 span은 같다. 방법은 다음과 같다.

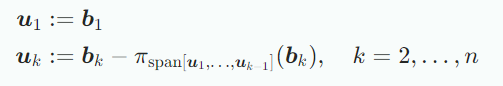
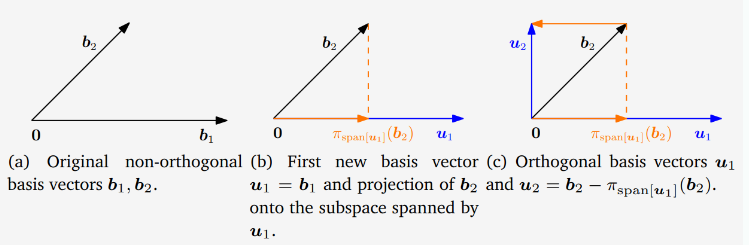
위의 식에서 k번째 기저벡터 $b_k$는 이전에 구한 k-1개의 orthogonal vector에 의해 span되는 subspace에 projection된다. 그 다음 $b_k$에서 이 projection을 빼 $u_k$를 구한다. 즉 $u_k$는 k-1개의 orthogonal vector에 의해 span되는 부분공간과 직교한다. 이 과정을 n개의 기저벡터에 대해 반복한다. $u_k$를 정규화하면 ONB를 구할 수 있다.($∥u_k∥=1$) 아래 그림은 예시다.

Projection onto Affine Subspaces

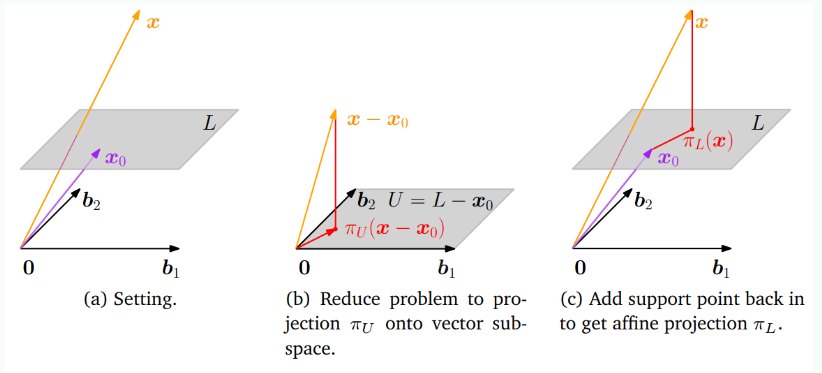
위의 그림을 보면 Affine space $L=x_0+U$가 주어지며 $U$의 기저벡터는 $b_1, b_2$이다. $L$에 투영되는 $π_L(x)$를 구할 때, vector subspace에 투영하는 문제로 변형하면 되는데 그림 (b)처럼 $x$와 $L$에서 support point $x_0$를 빼주면 부분공간 $U=L−x_0$을 얻을 수 있고 projection π_U(x−x_0)을 구한 후 다시 $x_0$를 더해 $L$로 변환하면 다음과 같이 $L$로의 정사영을 얻을 수 있다.

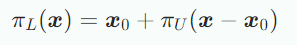
그림 (c)로부터 $L$과 $x$의 distance는 $x - x_0$사이의 distance와 같으며 식으로 표현하면 다음과 같다.