Ch3-2.Inner Products

Inner Products

내적은 벡터의 길이나 두 벡터 간의 각도 또는 거리 등과 같은 직관적인 기하학적 개념을 도입하기 위한 것이다.

Dot Product

내적의 한 타입인 scalar product/dot product는 다음과 같다.

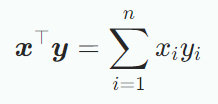
General Inner Products

bilinear mapping $Ω$는 두 인자에 대한 mapping 이며, 각 인자에 대해 linear한다. $x,y,z∈V$와 $λ,ψ∈R$에 대해 다음이 성립한다.

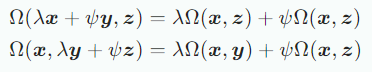
모든 $x, y∈V$에서 $Ω(x, y) = Ω(y,x)$라면 인자들의 순서가 상관이 없다는 뜻이고 symmertic이라고 부른다. 또한 아래 정의가 성립하면 positive definite라고 한다.

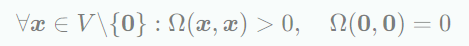
Positive definite이면서 symmetric bilinear mapping $Ω:V×V→R$를 $V$에서의 inner product라고 부르며 $⟨x,y⟩$로 쓴다.

Symmetric, Positive Definite Matrices

inner product $⟨⋅,⋅⟩:V×V→R$인 n차원 벡터공간 $V$와 기저 $B = (b_1,...., b_n)$가 있을 때, 모든 벡터 $x, y$는 basis vector의 선형결합으로 표현가능하므로 다음과 같다.

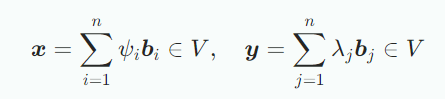
또한 Inner product의 bilinearlity 때문에 다음이 성립한다.

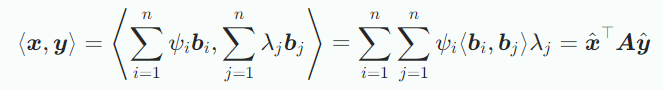
여기서 $A_{ij} :=⟨b_i, b_j⟩$이며 $\hat{x}, \hat{y}$는 기저 B에 대한 x, y의 좌표다.이는 inner product가 $A$를 통해 결정된다는 것을 의미한다. 또한, inner product의 positive definiteness는 다음이 성립한다는 것을 의미한다.

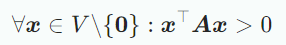
위를 만족하는 symmetric matrix $A∈R^{n×n}$를 symmetric, positive definite라고 하며, 항등식 $≥$가 성립하면, symmetric, positive semidefinite라고 한다.

$A$가 symmetric, positive definite라면, 아래의 식은 기저 $B$에 대한 inner product를 정의하며 $\hat{x}, \hat{y}$는 B에 대한 x, y의 좌표다.

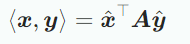
위의 식을 만족하는 symmetric, positive definite matrix $A∈R ^{n×n}$가 존재하면 다음의 성질들이 성립한다.

$A$의 null space는 오직 0으로만 구성된다.(x가 0이 아닌 모든 x에 대해 $x^TAx > 0$이므로) 즉, x가 0이 아니면 $Ax$도 0이 아니다. 또한 A의 대각 성분 $a_{ii} >0$이므로 positive다.