Ch3-3. Lengths and Distances

Lengths and Distances

내적을 통해 벡터의 길이를 계산할 수 있지만 모든 norm이 내적에 의해 유도되지는 않는다. (ex: Manhattan norm) 내적에 의해 유도되는 norm을 중심으로 lengths, distances, angles 같은 기하학적 개념을 살펴보자.

Inner product vector space ($V, ⟨⋅,⋅⟩$)에서 유도되는 norm$∥⋅∥$은 Cauchy-Schwarz inequality
$∣⟨x,y⟩∣≤∥x∥∥y∥$ 를 만족한다.

Inner product vector space ($V, ⟨⋅,⋅⟩$)에 속하는 x와 y의 distance는 다음과 같다.

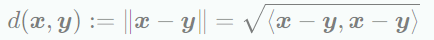
내적으로 dot product를 사용할 때, 이 distance를 Euclidean distance라고 한다. 그리고 metric 은 다음의 mapping으로 정의된다.

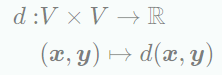
Metric d는 다음을 만족한다.

1. positive definite하다. 즉 모든 $x,y∈V$에 대해 $d(x,y)≥0$이며 $x=y$일 때 $d(x,y)=0$이다.
2. symmertic하다.즉 모든 $x,y∈V$에 대해 $d(x,y) = d(y,x)$이다.
3. Triangle inequality: 모든 $x,y, z∈V$에 대해 $d(x, z)≤d(x, y) + d(y,z)$이다.

벡터의 길이와 비슷하게, 벡터 간 거리는 내적을 필요로 하진 않고 norm만으로 충분하다. 내적으로부터 유도되는 norm이 있다면 distance는 선택된 내적에 따라 달라질 수 있다.